Kirchhoff’sche Gesetze

Kirchhoff’sches 1. Gesetz: Knotenregel

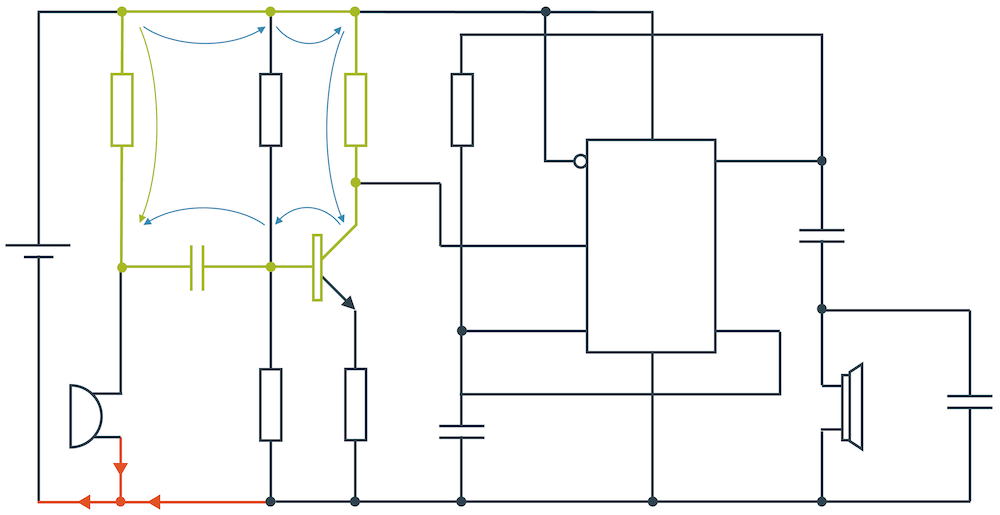
Das erste Gesetz von Kirchhoff wird auch Knotenregel genannt. Es geht hier um die Knoten, an welchen die Stromleiter sich aufteilen oder wieder zusammenkommen. Im unten abgebildeten Schaltplan sind zwei solche Knoten markiert.

Im ersten Knoten fliesst ein elektrischer Strom von \(0.9\,\text{A}\) auf den Knoten zu. Der Leiter teilt sich im Knoten auf in zwei Leiter. Der eine Leiter führt \(0.6\,\text{A}\) weg. Wegen der Ladungserhaltung muss der andere Leiter den Rest, d.h. \((0.9-0.6)\,\text{A} = 0.3\,\text{A}\) an Strom führen.

Im zweiten Knoten kommen zwei Ströme von \(0.3\,\text{A}\) zusammen. Der abführende Leiter muss deshalb einen Strom von \(0.6\,\text{A}\) haben.

Die Ladungserhaltung verlangt nämlich, dass Ladung weder erschaffen oder vernichtet werden kann. Sie kann nur verschoben bzw. weitergeleitet werden. Da im Leiter sich die Ladungen auch nicht akkumulieren können, muss die Summe aller Zuflüsse gleich der Summe aller Abflüsse entsprechen.

Beachte, dass Kondensatoren beim Aufladevorgang eine Akkumulation von Ladung zulassen – es ist ja ihr ureigener Zweck, Ladungen anzuhäufen. Genauso kann ein Kondensator seine gespeicherten Ladungen an den Schaltplan wieder abgeben, ohne dass sie im gleichen Moment zu ihm fliessen.

Kirchhoff’sches 2. Gesetz: Maschenregel

Das zweite Gesetz von Kirchhoff betrifft die elektrische Spannung. Sie wird auch Maschenregel genannt. Im nachfolgenden Schaltplan sind zwei solche Maschen.

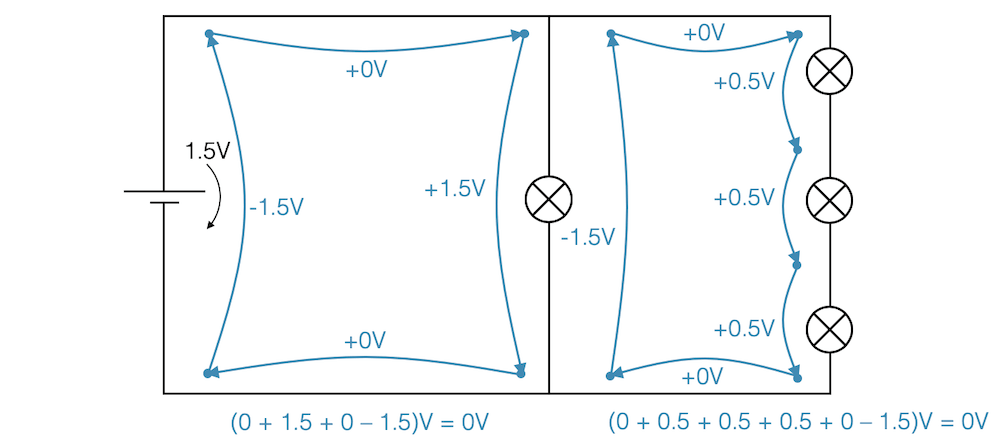
Die erste Masche ist der ”Stromkreis” in der linken Hälfte. Wir starten am Pluspol der Batterie. Das elektrische Potenzial ist da auf \(+1.5\,\text{V}\). Wenn wir von der linken oberen Ecke zur rechten oberen Ecke springen, fällt das elektrische Potenzial nicht. Es ist immer noch auf dem Niveau von \(+1.5\,\text{V}\). Die Potenzialdifferenz oder eben die elektrische Spannung von links oben nach rechts oben ist deshalb null.

Von oben rechts nach unten rechts fällt das Potenzial von \(+1.5\,\text{V}\) auf \(0\,\text{V}\) herunter. Das entspricht einer Potenzialdifferenz von \(+1.5\,\text{V}\). Wir schreiben deshalb \(+1.5\,\text{V}\) neben dem Pfeil, der nach unten zeigt. Es bedeutet, dass das elektrische Potenzial um \(+1.5\,\text{V}\) abnimmt.

Der nächste Sprung, von rechts unten nach links unten, ist wieder ein Sprung vom Niveau \(0\,\text{V}\) auf das Niveau \(0\,\text{V}\). Die elektrische Spannung bzw. Potenzialdifferenz beträgt deshalb \(0\,\text{V}\).

Schliesslich springen wir von unten links, über die Batterie, nach oben links. Hier nimmt die Spannung um \(1.5\,\text{V}\) zu. Da wir hier eine Zunahme des elektrischen Potenzials haben und wir eigentlich immer nur die Abnahmen aufschreiben, müssen wir \(-1.5\,\text{V}\) mit einem Minus versehen. Die Zunahme entspricht einer Abnahme um \(-1.5\,\text{V}\).

Damit haben wir die linke Masche geschlossen. Das Kirchhoff’sche 2. Gesetz besagt nun, dass wir nach einer Runde auf der Masche wieder auf dem gleichen elektrischen Potenzial liegen müssen. Die Spannungen müssen sich deshalb alle zu null summieren. Konkret: In der eben betrachteten Masche ist das Potenzial von \(+1.5\,\text{V}\) in der Lampe auf \(0\,\text{V}\) gefallen und in der Batterie wieder auf \(+1.5\,\text{V}\) angehoben werden.

Eine leicht abgeänderte Form der klassischen Maschenregel ist die Folgende: Wir betrachten wieder die linke Masche im Schaltplan. Wenn wir vom Pluspol der Batterie direkt zu ihrem Minuspol springen, so haben wir die Spannung der Batterie. Das elektrische Potenzial fällt von \(+1.5\,\text{V}\) auf \(0\,\text{V}\) ab, d.h. wir haben eine Spannung von \(+1.5\,\text{V}\) über der Batterie (rot).

Wenn wir mit dem gleichen Startpunkt und dem gleichen Endpunkt einen anderen Weg wählen, also auch vom Plus- zum Minuspol der Batterie, dieses Mal jedoch über die Lampe, dann muss die Spannung auch \(+1.5\,\text{V}\) sein (blau). Über dem Leiter fällt das elektrische Potenzial nicht ab, d.h. dort haben wir keine Spannung. Über die Lampe muss die Spannung aber \(+1.5\,\text{V}\) betragen.

Nehmen wir die zweite Masche (rechts): Hier springen wir ”im Gegenuhrzeigersinn” vom elektrischen Potenzial \(+1.5\,\text{V}\) bis an den unteren Anschluss der zweiten Lampe. Die elektrische Potenzial fällt über die Batterie um \(+1.5\,\text{V}\) auf \(0\,\text{V}\). Dann nimmt das elektrische Potenzial über der dritten Lampe wieder zu, wenn wir von unten kommen. Wir gehen hier vom Niveau \(0\,\text{V}\) auf das Niveau \(+0.5\,\text{V}\) hinauf. In Summe sind wir um \(1\,\text{V}\) abgefallen, d.h. die Summe der Spannungen auf diesem ”Mehrfachsprung” beträgt \(1\,\text{V}\) (rot).

Auf dem anderen Weg gehen wir vom Niveau \(+1.5\,\text{V}\) auf \(+0.5\,\text{V}\) herunter, d.h. eine Spannung von ebenfalls \(1\,\text{V}\).