Um die Verwendung des Konzepts des Ersatzwiderstands zu erklären, schauen wir uns ein Beispiel an. Wir suchen im folgenden Schaltplan die beiden Ströme \(I_1\) und \(I_2\). Das Problem, das sich dabei stellt: Welche Spannung liegt über den einzelnen Widerständen? Wie kombinieren wir verschiedene Widerstände?

Hätten wir nur einen Widerstand von \(R = 5\,\Omega\), so wäre es bei einer Spannung von \(U = 6\,\text{V}\) ein leichtes, den Strom zu berechnen. Mit dem ohm’schen Gesetz hätten wir:
\[ U = R \cdot I \quad \rightarrow \quad I = \frac{U}{R} = \frac{6\,\text{V}}{5\,\Omega} = 1.2\,\text{A} \]
Nach dem (blauen) Widerstand von \(R = 5\,\Omega\) folgt aber ein weiterer Widerstand. Die Spannung über dem \(R = 5\,\Omega\)-Widerstand wird nur ein Teil der \(6\,\text{V}\) sein und damit wird der Strom \(I_1\) kleiner sein als \(1.2\,\text{A}\).
Der (rote) Widerstand von \(R = 5\,\Omega\) liegt tatsächlich unter einer Spannung von \(6\,\text{V}\). Sein oberer Anschluss ist auf dem Potenzial von \(+6\,\text{V}\). Sein unterer Anschluss liegt auf dem Potenzial von \(0\,\text{V}\). Durch diesen Widerstand fliessen deshalb tatsächlich \(1.2\,\text{A}\). Neben ihm ist aber ein anderer Widerstand parallel geschaltet. Durch ihn fliesst auch ein Strom, d.h. \(I_2\) ist grösser als \(1.2\,\text{A}\).
Wir können die beiden blauen Widerstände mit einer einfachen Methode zu einem Widerstand umrechnen, so dass wir die einfache Rechnung machen können. Die beiden blauen Widerstände sind in Serie geschaltet und deshalb werden ihre Widerstandswerte einfach addiert: Die Summe der beiden Widerstände \(R_1\) und \(R_2\) ergeben den Ersatzwiderstand \(R_{tot}\) (totaler Widerstand).

Hätten wir nur einen Widerstand vom Wert \(R_{tot}\), so würde gleich viel Strom \(I_1\) durch ihn fliessen, wie durch die beiden Widerstände \(R_1\) und \(R_2\) in Serie:
\[ R_{tot} = R_1 + R_2 = 5\,\Omega + 20\,\Omega = 25\,\Omega \]
Wir stellen deshalb das ohm’sche Gesetz mit dem Ersatzwiderstand auf und erhalten so \(I_1\):
\[ I_1 = \frac{U}{R_{tot}} = \frac{6\,\text{V}}{25\,\Omega} = 0.24\,\text{A} \]
Wie sieht die Situation bei den roten Widerständen aus? Hier sind \(R_1\) und \(R_2\) parallel geschaltet. Das Addieren der Widerstandswerte wäre falsch, denn wir erleichtern ja den Stromfluss indem wir zwei statt nur einen möglichen Weg anbieten, auf welchem die Ladungen fliessen können. In Summe ist der Widerstand durch die beiden parallelen Widerstände erleichtert. Der Ersatzwiderstand muss kleiner sein als der kleinste der beiden Widerstände, also kleiner als \(5\,\Omega\)!
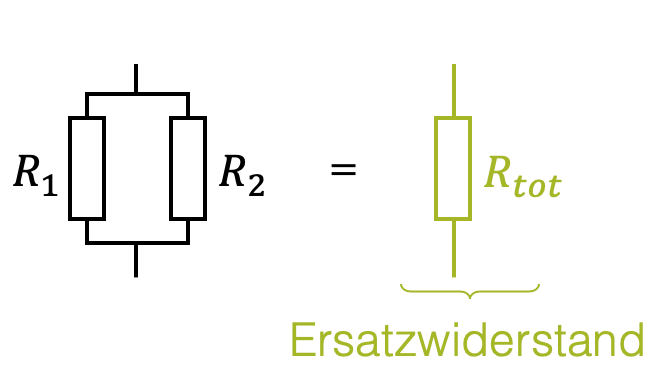
Bei parallelen Widerständen addiert man nicht die Widerstände selbst, sondern deren Kehrwerte. Achtung, nicht vergessen: Das Resultat ist ebenfalls der Kehrwert von \(R_{tot}\).
\[ \frac{1}{R_{tot}} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{5\,\Omega} + \frac{1}{20\,\Omega} = \frac{4+1}{20\,\Omega} \]
\[ \frac{1}{R_{tot}} = \frac{5}{20\,\Omega} = \frac{1}{4\,\Omega} \quad \rightarrow \quad R_{tot} = 4\,\Omega \]
Wir sehen, dass wir wirklich einen Wert erhalten, der kleiner als \(5\,\Omega\) ist. Wir können jetzt den Strom \(I_2\) berechnen:
\[ I_2 = \frac{U}{R_{tot}} = \frac{6\,\text{V}}{4\,\Omega} = 1.5\,\text{A} \]
Jetzt wissen wir natürlich, dass die Spannungsquelle einen totalen Strom von \(I_{tot} = I_1 + I_2 = 0.24\,\text{A} + 1.5\,\text{A} = 1.74\,\text{A}\) liefert. Es gibt aber auch hier die Möglichkeit, dies über den Ersatzwiderstand zu bestimmen. Der blaue und der rote Widerstand sind zueinander parallel geschaltet, d.h. wir können einen Ersatzwiderstand für die ganze Schaltung aufstellen:
\[ \frac{1}{R_{tot}} = \frac{1}{25\,\Omega} + \frac{1}{4\,\Omega} = \frac{4+25}{100\,\Omega} \]
\[ R_{tot} = \frac{100}{29}\,\Omega = 3.45\,\Omega \]
Die vier Widerstände verhalten sich gleich, wie ein einziger Widerstand von \(3.45\,\Omega\). Um den Strom zu berechnen, der durch die ganze Schaltung, also durch diesen Widerstand fliesst, stellen wir wieder das ohm’sche Gesetz auf:
\[ I_{tot} = \frac{U}{R_{tot}} = \frac{6\,\text{V}}{3.45\,\Omega} = 1.74\,\text{A} \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.