
Image by Christian Ladewig, shared on Unsplash
Die Coulombkraft (elektromagnetische Kraft) ist die zweitstärkste Kraft der vier Grundkräfte der Physik. Sie wirkt auf elektrische Ladungen anziehend, wenn beide Ladungen ungleiches Vorzeichen haben, oder abstossend, wenn beide Ladungen das gleiche Vorzeichen haben.
Die Coulombkraft \(F_C\) zwischen zwei Ladungen ist für beide Ladungen gleich gross im Betrag, jedoch umgekehrt in der Richtung. Mit Hilfe des Coulomb-Gesetzes kann der Betrag der Coulombkraft berechnet werden. Die Kraft ist proportional zu den Ladungen und umgekehrt proportional zum Quadrat des Abstands der beiden Ladungen:
\[ F_C = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]
Für Umrechnung der Einheiten wird der konstante Umrechnungsfaktor verwendet: \(\;\;k \approx 9.0 \cdot 10^9 \; \frac{\text{N}\,\text{m}^2}{\text{C}^2}\).
Wirken mehrere Ladungen, so werden die einzelnen Coulombkräfte separat berechnet und als Kraftvektoren addiert. Die Zusammenfassung aller Coulombkräfte für die verschiedenen Orte im Raum wird als elektrisches Feld verstanden.
Die Coulombkraft hat für unser tägliches Leben eine weit bedeutendere Rolle als wir das auf den ersten Blick vermuten würden. Die elektromagnetische Kraft ist auch bekannt als Coulombkraft, benannt nach dem französischen Physiker Charles Augustin de Coulomb (1736 – 1806). Er gilt als einer der Begründer der Elektrostatik und der Magnetostatik indem er experimentell das elektrostatische Kraft-Abstand-Gesetzes demonstrierte (Coulomb-Gesetz).
“Consider a force like gravitation … but which is about a billion-billion-billion-billion times stronger. And with another difference. There are two kinds of „matter“, which we can call positive and negative. … What would happen?
There is such a force: the electrical force. With such an enormous force … it is not hard to understand that matter can have great stiffness and strength. The Empire State Building, for example, swings only eight feet in the wind because the electrical forces hold every electron and proton more or less in its proper place.”
Image, author unknown, public domain
Die Kraft zwischen Atomen, die zur Bildung von Molekülen führt oder zu Atomgittern, z.B. in Metallen oder Gesteinskristallen, ist die Coulombkraft. Dank ihr gibt es überhaupt die Feststoffe und damit auch eine Erdkruste, auf welcher wir leben! Wie die Kraft die Materie zusammenhält, ist auf einen quantenmechanischen Effekt zurückzuführen und wird hier nicht besprochen. Wir werden uns auf die einfache anziehende und abstossende Wechselwirkung der elektrischen Ladung beschränken.
Anziehung und Abstossung
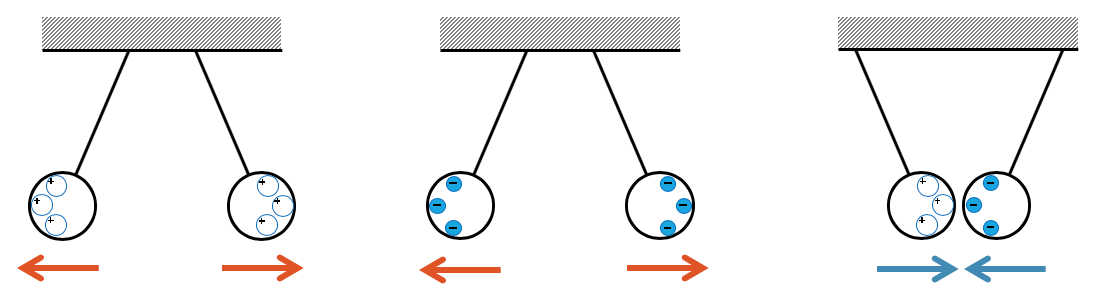
Im Gegensatz zur Gravitationskraft, die nur anziehend wirkt, kann die Coulombkraft anziehend oder auch abstossend wirken.
Werden zwei hängende Metallkugeln positiv geladen, so wirkt die Coulombkraft auf die positiven Ladungen, so dass sie sich gegenseitig abstossen. Positive Ladungen sind als positiv geladene Löcher im Metall beweglich. Sie bewegen sich deshalb in allen Richtungen von einander weg. Allerdings sind sie an das Metall gebunden und können die Kugeln nicht verlassen.
Die positiven Löcher an den beiden äusseren Enden sind Atome, denen Elektronen fehlen. Die positive Ladung der Atomkerne wirkt abstossend auf die positive Ladung der anderen unterbesetzten Atomkerne auf der anderen Kugel und umgekehrt. Die Kraft wirkt auf die Atomkerne und damit auf die ganze Kugel, so dass beide Kugeln sich auseinander bewegen. Sie tun das, bis die dagegen wirkende Fadenkraft gleich gross ist und damit die resultierende Kraft pro Kugel null wird.
Bei den negativ geladenen Kugeln haben wir den gleichen Effekt. Die Elektronen stossen sich gegenseitig ab und “fliehen” auf die äusseren Seiten der beiden Kugeln. Allerdings können sie dann nicht mehr weiter. Die abstossenden Kräfte wirken immer noch und zieht an ihnen. Sie sind aber weiterhin an die Atomkerne in ihrer Nähe gebunden. Sie ziehen an ihnen und damit auch am ganzen Gitter bzw. an der ganzen Kugel.
Zwei Kugeln, die ungleich geladen sind, zeigen ein umgekehrtes Verhalten. Die beiden Kugeln ziehen sich an.
Falls sie sich kurzzeitig berühren, gleichen sich die Ladungen aus und die Wirkung verschwindet. War von einer Art Ladung mehr vorhanden als von der anderen Art, so bleibt nach der Berührung immer noch Ladung übrig. Nach der Berührung sind beide Kugeln gleich geladen, die Ladungen verteilen sich wieder und die Kugeln stossen sich wieder ab.
Coulombs Gesetz
Charles Augustin de Coulomb fand experimentell heraus, dass die anziehende oder abstossende Kraft dem gleichen Gesetz folgt, wenn es um ihren Betrag \(F_C\) geht. Wir können deshalb das Vorzeichen der Ladungen ignorieren und die Stärke der Kraft berechnen. Erst am Schluss müssen wir wieder die Richtung der Kraft berücksichtigen, je nachdem ob es sich um gleiche oder ungleiche Ladungen handelt.
Je stärker die beiden Ladungen \(q_1\) und \(q_2\), desto stärker ist die Coulombkraft. Sie ist proportional zu den Ladungen, d.h. wenn wir eine der beiden Ladungen verdoppeln, verdoppelt sich auch die Kraft.
Beachte auch, dass die Coulombkraft \(F_C\) für beide Ladungen gleich gross ist. Man könnte erwarten, dass eine grössere Ladung eine grössere Kraft erfährt. Die Ladungen wirken aber aufeinander. Gemäss Newtons Drittem Gesetz ist die Wechselwirkung gleich im Betrag, jedoch entgegengesetzt in der Richtung. Wenn wir also beispielsweise eine der beiden Ladungen verdoppeln, so verdoppelt sich die Kraft für beide Ladungen, weil sie immer gleich im Betrag ist. Die eine Ladung stösst mehr ab und die andere wird mehr abgestossen.
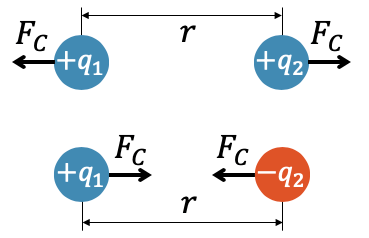
Die Coulombkraft zeigt auch eine starke Abhängigkeit vom Abstand. Wie bei der Gravitationskraft ist die Coulombkraft umgekehrt proportional zum Quadrat des Abstands, der auch hier mit \(r\) abgekürzt wird. Verdoppeln wir den Abstand, so halbiert sich nicht die Kraft, sondern wird \(2^2\)-mal, also vier mal schwächer. Damit erhalten wir Coulombs Gesetz:
\[ F_C = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]
Für Umrechnung der Einheiten wird ein konstanter Umrechnungsfaktor vorgeschaltet: \(\;\;k = 8.9876 \cdot 10^9 \; \frac{\text{N}\,\text{m}^2}{\text{C}^2} \;\; \approx \;\; 9.0 \cdot 10^9 \; \frac{\text{N}\,\text{m}^2}{\text{C}^2}\).
In den meisten Lehrbüchern wird nicht die Konstante \(k\) verwendet, sondern der folgende Ausdruck:
\[ k = \frac{1}{4 \pi \epsilon_0} \]
Dabei ist \(\epsilon_0\) die Dielektrizitätskonstante für das Vakuum: \(\epsilon_0 = 8.854 \cdot 10^{-12}\;\frac{\text{A}\,\text{s}}{\text{V}\,\text{m}}\). Für unsere Bedürfnisse ist es weit praktischer, mit einer Konstante \(k\) zu arbeiten.
Beispiel
Wie viel beträgt die anziehende Kraft zwischen einem Elektron und einem Proton in einem Wasserstoffatom?
Ladung des Elektrons: \(q_e = −1.602 \cdot 10^{−19}\;\text{C}\)
Mittlerer Radius des Wasserstoffatoms (Bohr-Radius): \(a = 5.292 \cdot 10^{−11}\;\text{m}\)
Wir setzen die Grössen ein. Beachte, dass das Proton die gleiche Einheitsladung \(q_e\) hat wie das Elektron, jedoch mit positivem Vorzeichen. Für die Berechnung der Coulombkraft brauchen wir das Vorzeichen nicht zu berücksichtigen. Wir stellen einfach fest, dass es sich um eine anziehende Coulombkraft handelt.
\[ F_C = k \cdot \frac{|q_e \cdot q_e|}{a^2} = k \cdot \frac{q_e^2}{a^2} \]
Jetzt setzen wir ein:
\[ F_C = 9.0 \cdot 10^9 \; \frac{\text{N}\,\text{m}^2}{\text{C}^2} \cdot \frac{(1.602 \cdot 10^{−19}\;\text{C})^2}{(5.292 \cdot 10^{−11}\;\text{m})^2} = 8.25 \cdot 10^{−8}\;\text{N} \]
Auch wenn diese Kraft jetzt sehr klein erscheint, so ist sie doch riesengross: Ein Mol Wasserstoff entspricht bei Normbedingungen (0 °C, 1.01325 bar Druck) einem Volumen von 22.4 Litern bzw. einer Masse von ca. 1 g. Die Gewichtskraft des Gases ist in der Grössenordnung von \(10^{-2}\) N. Wir haben in diesem Gas aber \(N_A=6.022\cdot10^{23}\) Wasserstoffatome und damit gleich viele Elektronen. Die eben berechnete Kraft für ein Elektron, multipliziert mit der Anzahl Elektronen gibt uns eine Coulombkraft von \(5 \cdot 10^{16}\) N! Mit einer solchen Kraft müssten wir ziehen, wenn wir alle Elektronen von ihren Protonen wegnehmen möchten.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.