
Der dänische Physiker und Chemiker Hans Christian Ørsted (1777 – 1851) entdeckte im Jahre 1820, wohl mehr aus Zufall, dass sich Kompassnadeln in der Nähe eines elektrischen Leiters bewegten, wenn er den Strom ein- und ausschaltete. Er hatte damit als Erster die Verbindung zwischen der Welt der Elektrizität und des Magnetismus festgestellt.
Tatsächlich bewirkt eine elektrischer Strom in einem geraden Leiter ein Magnetfeld, das um den Leiter herum kreist. Die Richtung des Magnetfelds ist senkrecht zum Leiter. Je näher zum Leiter, desto stärker ist dieses Magnetfeld. Die Umlaufrichtung folgt ebenfalls einer Gesetzmässigkeit, denn wenn wir den Strom umkehren, kehrt auch die Richtung des kreisförmigen Magnetfelds um.
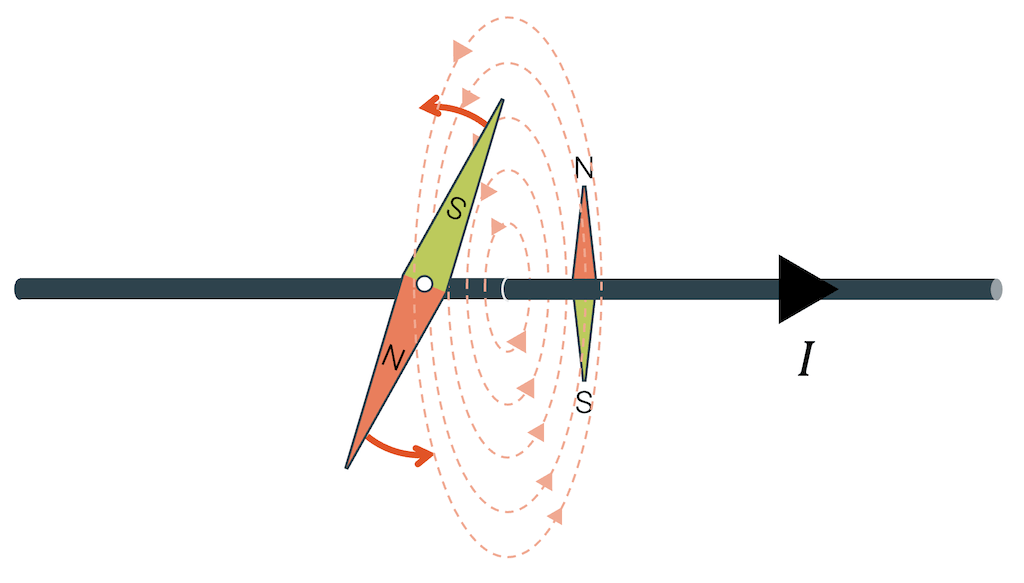
Rechte-Hand-Regel für die Richtung des Magnetfelds
Wir können die kreisförmigen Feldlinien des Magnetfelds mit Hilfe von Eisenfeilspänen (siehe Bild) sehr schön zeigen. Für die Richtung des Magnetfelds braucht es jedoch Kompassnadeln. Wir können die Drehrichtung des Magnetfelds auch mit der Rechte-Hand-Regel bestimmen, sofern wir die Richtung des elektrischen Stroms kennen. Dazu setzen wir den Daumen in die Richtung des elektrischen Stroms \(I\) und lesen die Richtung des Magnetfelds \(B\) von den übrigen Fingern ab.
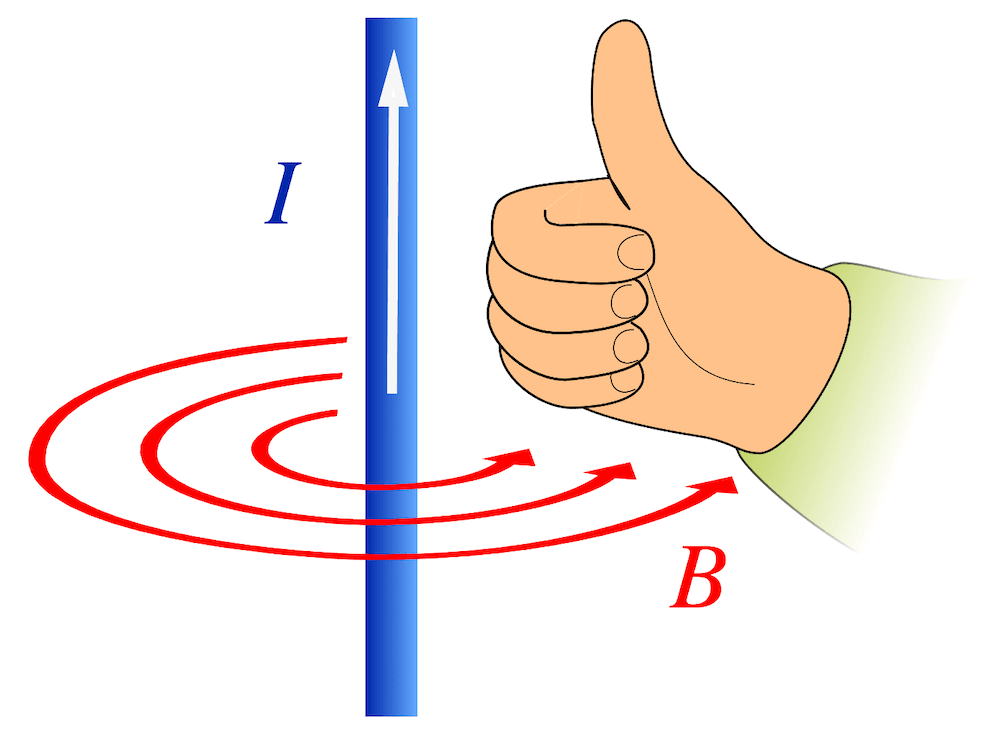
Illustration of the right hand rule by Jfmelero, licensed under CC BY-SA 4.0
Die ein mit einem Strom \(I\) durchflossenen Leiter erzeugt ein, um den Leiter drehendes Magnetfeld, wobei die Richtung mit der Rechte-Hand-Regel bestimmt werden kann:
- Daumen = Richtung des Stroms (Fliessrichtung der positiven Ladungen)
- übrige, gekrümmte Finger = Richtung des Magnetfelds \(B\)
Die Stärke des Magnetfelds nimmt mit zunehmendem Abstand vom Leiter ab.
Berechnung der Stärke des Magnetfelds
Aus den Maxwell’schen Gleichungen folgt, vereinfacht:
Stärke des Magnetfelds im Abstand \(r\) zu einem (unendlichen) geraden Leiter:
\[ B(r) = \mu_0 \cdot \frac{I}{2 \pi r} \]
Der Leiter muss natürlich nicht unendlich lange sein, aber er muss viel länger sein als der Abstand, der berechnet wird (\(l>>r\)).
Das Magnetfeld um einen geraden Leiter besteht aus kreisförmigen Feldlinien. Es kommt nicht darauf an, wo auf dem Kreis, sondern wie weit wir uns vom Leiter befinden. Deshalb ist die Stärke des Magnetfelds eine Funktion des Radius \(r\), dem Abstand zum Leiter. \(I\) ist der elektrische Strom, der durch den Leiter fliesst.
Die magnetische Feldkonstante \(\mu_0\) ist eine Naturkonstante:
\[ \mu_0 = 4\pi \cdot 10^{-7} \;\frac{\mathrm{Vs}}{\mathrm{Am}} \]
Betrachten wir das Magnetfeld nicht im Vakuum, sondern in einem Stoff, so müssten wir zusätzlich mit der magnetischen Permeabilität \(\mu_r\) des betreffenden Stoffs multiplizieren. Wir werden uns hier auf Magnetismus in Luft beschränken. Die magnetische Permeabilität von Luft ist \(\mu_r \approx 1\), so dass wir den magnetischen Einfluss der Luft vernachlässigen können.
Im folgenden Beispiel betrachten wir zwei Leiter, durch welche die gleichen Ströme \(I\) mit gleicher Richtung fliessen. Das Magnetfeld \(B_1\) im Abstand \(r_1\) vom oberen Leiter ist halb so stark, die das Magnetfeld \(B_2\) vom unteren Leiter im Abstand \(r_2\). Mit Hilfe der Rechte-Hand-Regel sehen wir auch, dass beide Magnetfelder im betrachteten Punkt die entgegengesetzte Richtung haben.
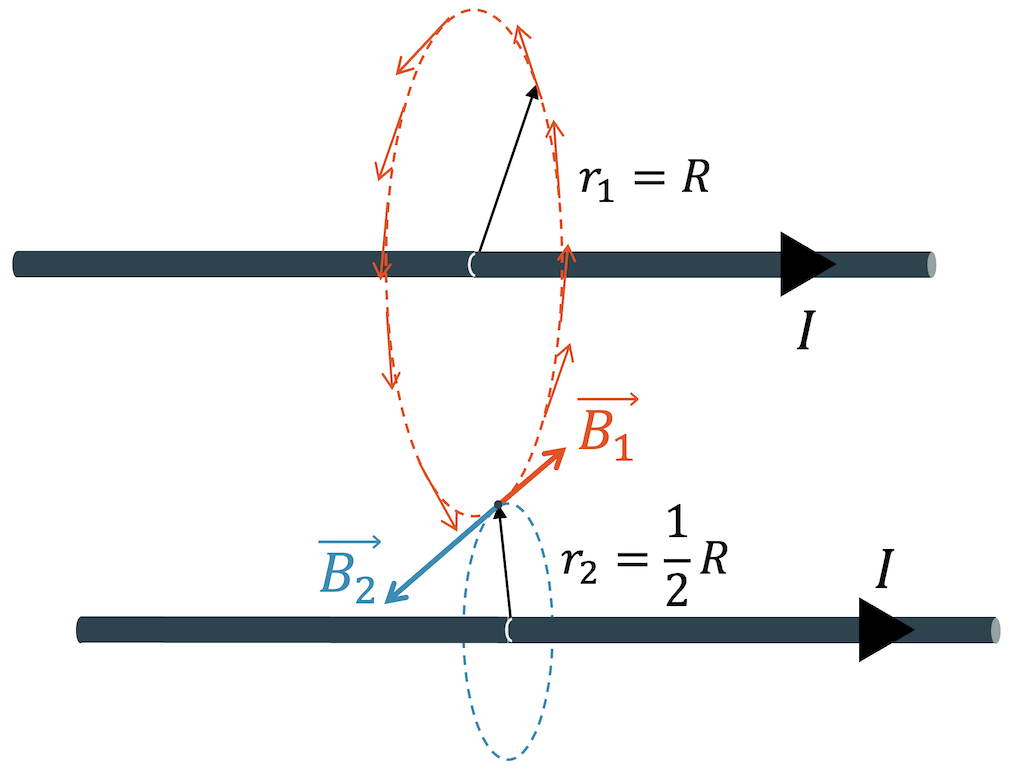
Eine Kompassnadel, die genau in diesem Punkt platziert wäre, würde beide Magnetfelder gleichzeitig erfahren. Es ist aber nicht so, dass sie jetzt hin und her drehen würde, sondern die beiden Magnetfelder werden überlagert und die Kompassnadel spürt nur das eine Magnetfeld, nämlich die Vektorsumme der beiden Magnetfelder \(\vec{B}_1\) und \(\vec{B}_2\).
\[ \vec{B} = \vec{B}_1 + \vec{B}_2 \]
In diesem speziellen Fall hätten wir zum einen einen Beitrag nach hinten (\(\vec{B}_1\)) und zum anderen einen doppelt so grossen Beitrag nach vorne (\(\vec{B}_2\)). In Summe bleibt somit ein einfacher Beitrag nach vorne in Richtung von \(\vec{B}_2\), jedoch halb so stark wie \(\vec{B}_2\), da die andere Hälfte vom Feld \(\vec{B}_1\) neutralisiert wird.
Relativität in der Elektrodynamik
Albert Einstein (1879-1955), gilt als einer der bedeutendsten theoretischen Physiker der Wissenschaftsgeschichte. Seine spezielle Relativitätstheorie fand ihre Wurzeln in der Elektrodynamik. Wir schauen uns nur kurz einen besonders interessanten Aspekt an.
Das Experiment von Ørsted war einfach ein gerader Leiter, durch welchen ein elektrischer Strom floss. Wir können uns den elektrischen Strom als die Bewegung denken, von positiv geladenen Löchern von links nach rechts mit einer Geschwindigkeit \(v_L\). Den metallischen Leiter darum herum, lassen wir zur Vereinfachung weg. Dieser Strom baut offenbar ein Magnetfeld auf und bewirkt, dass die ruhende Kompassnadel (\(v_N = 0\)) sich nach ihm ausrichtet.
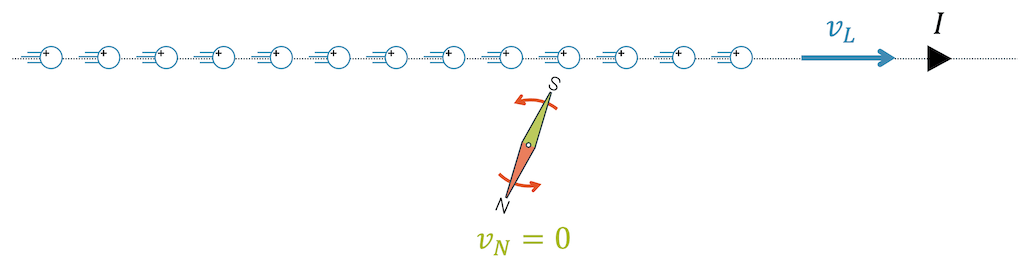
Jetzt ändern wir nur die Betrachtungsweise, ändern aber an der Physik gar nichts. Wir bewegen uns als Beobachter zusammen mit den Ladungen und sehen jetzt eine Kompassnadel, die sich mit der Geschwindigkeit \(v_N\) nach links an uns vorbeibewegt. Die Ladungen stehen still (\(v_L=0\)). Ruhende Ladungen gehören in das Gebiet der Elektrostatik, d.h. es sind viele Punktladungen, die jede für sich ein elektrisches Feld aufbauen.
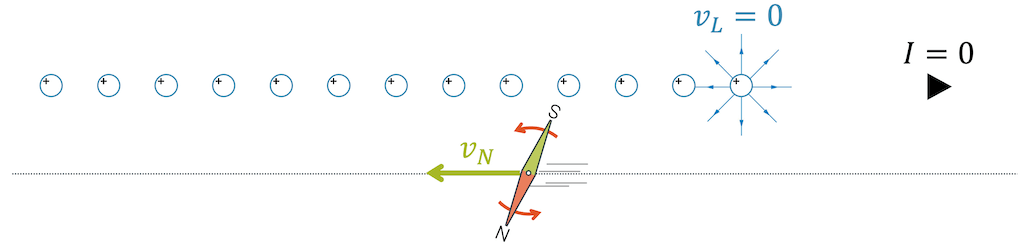
Wir haben wirklich nichts als der Betrachtung verändert. Wenn ein Zug mit 50 km/h durch einen Bahnhof fährt, dann sehen die Fahrgäste im Zug einen Bahnhof, der mit 50 km/h an ihnen vorbeiflitzt. Beides ist richtig. Die “Ruhe” ist nicht dem Bahnhof vorbehalten. Wir dürfen durchaus unser Koordinatensystem in den Zug legen und alles von hier aus beschreiben. Dann bewegt sich alles, ausser der Zug selbst.
In unserem obigen Beispiel heisst das: Eine Kompassnadel, die an einer ruhenden Ladung vorbeiflitzt, wird ein Magnetfeld spüren und sich danach ausrichten! Die Ladungen erzeugen aber nur ein elektrisches Feld. Das Magnetfeld entsteht aber, wenn die Kompassnadel sich im elektrischen Feld bewegt. Deshalb können wir das Experiment von Ørsted verallgemeinern:
Es ist nicht die elektrische Ladung, die sich unbedingt bewegen muss (elektrischer Strom), um ein Magnetfeld zu erzeugen, sondern ein Beobachter kann auch ein Magnetfeld erfahren, wenn er sich relativ zu elektrischen Ladungen und deren elektrischem Feld bewegt.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.