Das Wichtigste in Kürze

Zwei Vektoren heissen kollinear, wenn sie zu einander parallel sind. Sie haben die gleiche Richtung oder sind exakt entgegengesetzt.

Der eine Vektor ist ein Vielfaches des anderen Vektors, d.h. die folgende Gleichung kann aufgestellt werden für einen bestimmten Wert für den Faktor \(k\):

\[ \vec{v} = k \cdot \vec{w} \]

Wir können die Vektoren in eine gemeinsame Gerade \(g\) verschieben.

Hack

Schau, ob Dir das Verhältnis der Komponenten untereinander an, z.B. ist das Verhältnis der x- zur y- zur z-Komponente hier 1:3:2

\[ \vec{a} = \begin{pmatrix} 10 \\ 30 \\ 20 \end{pmatrix} \]

Somit ist der Vektor \(\vec{b}\) kollinear zu \(\vec{a}\), weil er auch das Verhältnis 1:3:2 unter seinen Komponenten hat:

\[ \vec{b} = \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix} \]

Besonders praktisch sind Vektorkomponenten, die null sind. Wir erkennen sofort, dass andere Vektoren kein Vielfaches sein können, wenn sie in der gleichen Komponente keine null haben.

Videos

  • Kollineare Vektoren (Short)

  • Kollinearität und Komplanarität mit Vektor- und Spatprodukt (5044-6)

    Dauer: 13 min 31 s

  • Analyse von Kollinearität und Komplanarität (5034-1)

    Dauer: 13 min 14 s

  • Analyse von Kollinearität und Komplanarität (5034-2)

    Dauer: 12 min 09 s

  • Kollinearität (Teil 1) (Tutorial)

    Dauer: 6 min 51 s

  • Kollinearität (Teil 2) (Tutorial)

    Dauer: 6 min 50 s

Häufigste Fragen

Ein Vektor alleine kann nicht kollinear sein…kollinear womit? Genauso wenig kann ein Vektor alleine nicht parallel sein.

Zwei oder mehr Vektoren können kollinear sein, wenn sie in eine gemeinsame Linie verschoben werden können, d.h. wenn sie gleich gerichtet oder exakt entgegengesetzt gerichtet sind.

Solche Vektoren sind ein Vielfaches der anderen Vektoren, denn durch die Multiplikation mit einem Skalar (Zahl) wird der Vektor verlängert, verkürzt oder kehrt sein Richtung um. Er bleibt aber immer in der gleichen Linie.

Überprüfe, ob der eine Vektor ein Vielfaches des anderen Vektors ist, d.h. jede Komponente muss das Vielfache der anderen Komponente sein, immer mit dem gleichen Vielfachen.

Wenn die beiden Vektoren \(\vec{v}\) und \(\vec{w}\) kollinear sind, dann gibt es einen Faktor (das Vielfache), so dass die folgende Gleichung erfüllt ist:

\[ \vec{v} = k \cdot \vec{w} \]

Gewissermassen. Vektoren haben noch eine Richtung und somit können parallele Vektoren gleich gerichtet oder exakt entgegengesetzt gerichtet sein.

Kollinearität grafisch erkennen

“Kollinear” steht für “ko” (gemeinsam” und “linear” (Linie). Kollineare Vektoren können in eine gemeinsame Linie oder Gerade verschoben werden.

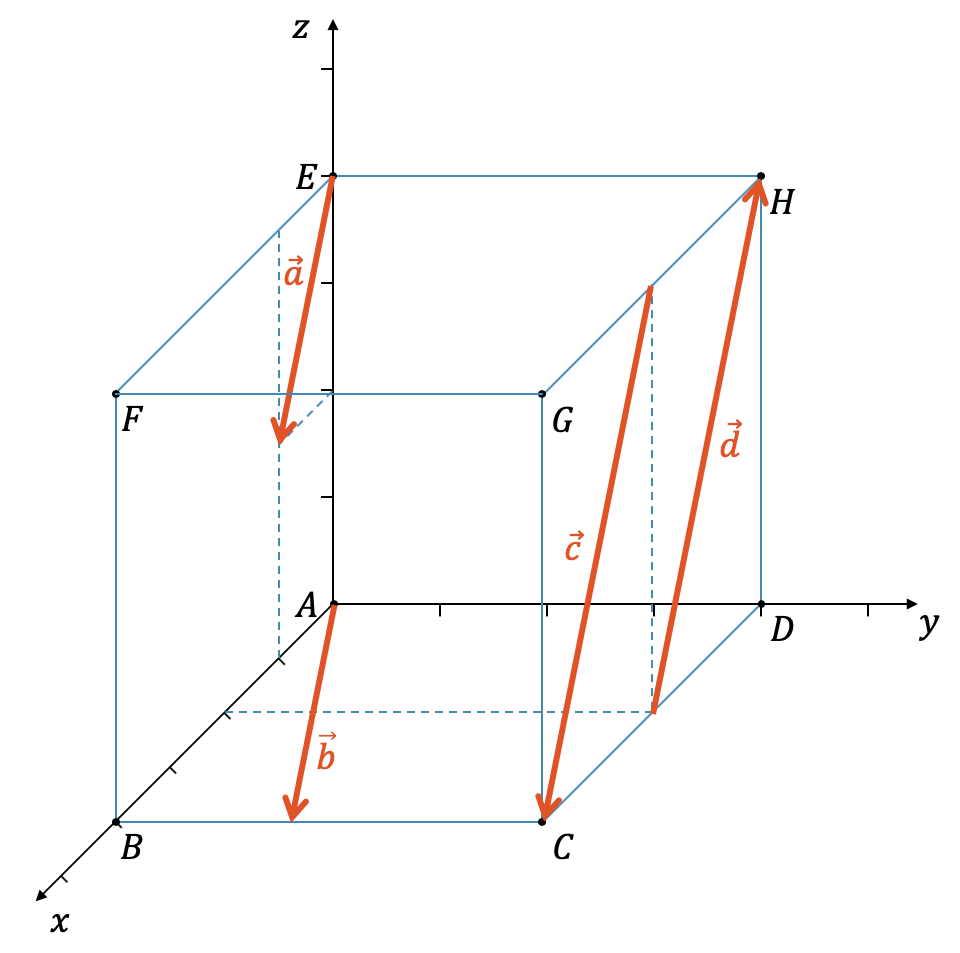
In der obigen Figur sind vier Vektoren gezeichnet, deren Start- und Endpunkte sich auf den Würfelflächen befinden.

Die Vektoren \(\vec{a}\) und \(\vec{c}\) haben die gleiche Richtung. Sie sind zwar unterschiedlich lang, aber eine Verdoppelung von \(\vec{a}\) ergibt genau \(\vec{c}\):

\[ 2\vec{a} = \vec{c} \]

Die Vektoren \(\vec{c}\) und \(\vec{d}\) sind auch kollinear. Sie sind gleich lang und einander entgegengesetzt.

\[ \vec{c} = -\vec{d} \]

Der Vektor \(\vec{b}\) erscheint fast gleich wie der Vektor \(\vec{a}\). Das liegt aber an der perspektivischen Darstellung. Eigentlich haben sie eine ganz andere Richtung. \(\vec{a}\) liegt in der \(x,z\)-Ebene und der Vektor \(\vec{b}\) liegt in der \(x,y\)-Ebene.

Die Vektoren \(\vec{a}\), \(\vec{c}\) und \(\vec{d}\) sind untereinander kollinear. Der Vektor \(\vec{b}\) ist mit keinem dieser Vektoren kollinear.

Kollinearität mit den Vektorkomponenten untersuchen

Wenn wir kein Bild der Vektoren haben, können wir ihre Kollinearität auch an ihren Komponenten erkennen:

\[ \vec{a} = \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 4 \\ 1.5 \\ 0 \end{pmatrix} \]

\[ \vec{c} = \begin{pmatrix} 2 \\ 0 \\ -4 \end{pmatrix}, \quad \vec{d} = \begin{pmatrix} -2 \\ 0 \\ 4 \end{pmatrix} \]

Als Erstes solltest Du die Nullen anschauen. Alle Vektoren \(\vec{a}\), \(\vec{c}\) und \(\vec{d}\) haben eine y-Komponente, die null ist, d.h. sie könnten untereinander kollinear sein.

Der Vektor \(\vec{b}\) hat auch eine Null, aber in der z-Komponente. Vielfache von \(\vec{b}\) werden alle die Null in der z-Komponente behalten, d.h. es ist unmöglich mit einem Vielfachen, einen der Vektoren \(\vec{a}\), \(\vec{c}\) oder \(\vec{d}\) zu erhalten.

Wir können deshalb den Vektor \(\vec{b}\) bereits jetzt ausschliessen. Er ist mit keinem der anderen drei Vektoren kollinear.

Jetzt schauen wir die Verhältnisse der Komponenten bei den drei Vektoren an. Sie sind alle gleich:

\[ 1 \;\; : \;\; 0 \;\; : \;\; (-2) \]

Das allein macht sie schon kollinear. Wir finden aber auch, dass die Vektoren Vielfache von einander sind:

\[ \vec{a} = \frac{1}{2} \cdot \vec{c} \]

\[ \vec{c} = (-1) \cdot \vec{d} \]

Somit haben wir in beiden Fällen einen Faktor \(k\) gefunden und deshalb ist erwiesen, dass sie kollinear sind.

Beispiel: Kollineare Vektoren finden

Welche der folgenden Vektoren sind kollinear?

\[ \vec{a} = \begin{pmatrix} -1 \\ -1.5 \\ -0.5 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \]

\[ \vec{c} = \begin{pmatrix} 3 \\ 6 \\ 9 \end{pmatrix}, \quad \vec{d} = \begin{pmatrix} -0.5 \\ -1 \\ 1.5 \end{pmatrix} \]

\[ \vec{e} = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} \]

Wir sehen, dass beim Vektor \(\vec{a}\) alle drei Komponenten das gleiche Vorzeichen haben. Das ist bei den anderen Vektoren auch der Fall, ausser bei \(\vec{d}\). Der Vektor \(d\) kann deshalb nicht kollinear sind mit allen anderen Vektoren.

Wir vergleichen jetzt die Komponenten untereinander. Die dritte Komponente ist die Kleinste. Verdoppeln wir sie, erhalten wir die erste Komponente. Verdreifacht, gibt es die zweite Komponente. Wir sehen, dass der Vektor \(\vec{e}\) die gleichen Verhältnisse unter seinen Komponenten hat. Es gilt:

\[ -\frac{1}{2} \cdot \vec{e} = -\frac{1}{2} \cdot \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} = \begin{pmatrix} -\frac{1}{2} \cdot 2 \\ -\frac{1}{2} \cdot 3 \\ -\frac{1}{2} \cdot 1 \end{pmatrix} = \begin{pmatrix} -1 \\ -1.5 \\ -0.5 \end{pmatrix} = \vec{a} \]

Jetzt schauen wir uns den Vektor \(\vec{b}\) an. Die Verhältnisse von der ersten zur zweiten und zur dritten Komponente betragen \(1\) : \(2\) : \(3\). Wir können deshalb für \(\vec{b}\) und \(\vec{c}\) schreiben: 

\[ \frac{1}{3} \cdot \vec{c} = \frac{1}{3} \cdot \begin{pmatrix} 3 \\ 6 \\ 9 \end{pmatrix} = \begin{pmatrix} \frac{1}{3} \cdot 3 \\ \frac{1}{3} \cdot 6 \\ \frac{1}{3} \cdot 9 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \vec{b} \]

Damit sind \(\vec{a}\) und \(\vec{e}\) kollinear. Die Vektoren \(\vec{b}\) und \(\vec{c}\) sind miteinander ebenfalls kollinear. Der Vektor \(\vec{d}\) ist mit keinem der anderen Vektoren kollinear.

Beispiel: Welche Punkte liegen auf einer gemeinsamen Geraden?

Finde die drei Punkte, die auf einer gemeinsamen Geraden im Raum liegen.

\[ A(1, -1, -1), \quad B(10,-7,2), \quad C(4, -3, 1), \quad D(-5, 3, -3) \]

Wir nehmen jetzt mal an, dass \(A\) auf der Geraden liegt und versuchen herauszufinden, welches die zwei anderen Punkte sind. Falls schon \(A\) nicht auf der Geraden war, merken wir es dann schon.

Wir stellen drei Verbindungsvektoren auf:

\[ \overrightarrow{AB} = \begin{pmatrix} 10 – 1 \\ -7 – (-1) \\ 2 – (-1) \end{pmatrix} = \begin{pmatrix} 9 \\ -6 \\ 3 \end{pmatrix} \]

\[ \overrightarrow{AC} = \begin{pmatrix} 4 – 1 \\ -3 – (-1) \\ 1 – (-1) \end{pmatrix} = \begin{pmatrix} 3 \\ -2 \\ 0 \end{pmatrix} \]

\[ \overrightarrow{AD} = \begin{pmatrix} -5 – 1 \\ 3 – (-1) \\ -3 – (-1) \end{pmatrix} = \begin{pmatrix} -6 \\ 4 \\ -2 \end{pmatrix} \]

Jetzt fällt uns auf, dass der zweite Vektor als einziger eine Komponente hat, die null ist. Damit ist es ausgeschlossen, dass die anderen zwei Vektoren mit \(\overrightarrow{AC}\) kollinear sein können, denn jedes Vielfache von \(\overrightarrow{AC}\) wird immer noch die gleiche Komponente gleich null haben.

Damit können wir den Punkt \(C\) ausschliessen.

Wenn \(\overrightarrow{AB}\) und \(\overrightarrow{AD}\) kollinear sind, liegen die drei Punkte auf einer Geraden. Dazu versuchen wir die Gleichung aufzustellen:

\[ \overrightarrow{AB} \stackrel{?}{=} k \cdot \overrightarrow{AD} \]

\[ \overrightarrow{AB} = \begin{pmatrix} 9 \\ -6 \\ 3 \end{pmatrix} \stackrel{?}{=} k \cdot \begin{pmatrix} -6 \\ 4 \\ -2 \end{pmatrix} \]

Nehmen wir die erste Komponente. Die Gleichung heisst hier:

\[ 9 \stackrel{?}{=} k \cdot -6 \]

Die Lösung ist \(k=-\frac{3}{2}\). Jetzt setzen wir diesen Wert in die anderen beiden Komponenten ein und schauen, ob die Gleichungen erfüllt sind:

\[ -6 \stackrel{?}{=} -\frac{3}{2} \cdot 4 \]

\[ 3 \stackrel{?}{=} -\frac{3}{2} \cdot -2 \]

Das ist so! Das heisst, es gibt ein \(k\) und die beiden Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AD}\) sind Vielfache von einander.

\[ \begin{pmatrix} 9 \\ -6 \\ 3 \end{pmatrix} = -\frac{3}{2} \cdot \begin{pmatrix} -6 \\ 4 \\ -2 \end{pmatrix} \]

\[ \overrightarrow{AB} = -\frac{3}{2} \cdot \overrightarrow{AD} \]

Deshalb sind die Punkte \(A\), \(B\) und \(D\) auf der gleichen Geraden im Raum.

Aufgabensammlung

  • Analysieren und Kombinieren von Vektoren (5034) – Aufg. 1

    5 Teilaufgaben (pdf/Video-Lösung):
    Analyse von Kollinearität und Komplanarität

    zur Aufgabe

  • Analysieren und Kombinieren von Vektoren (5034) – Aufg. 2

    6 Teilaufgaben (pdf/Video-Lösung):
    Analyse von Kollinearität und Komplanarität

    zur Aufgabe

  • Vektor- und Spatprodukt (5044) – Aufg. 6

    2 Teilaufgaben (pdf/Video-Lösung):
    Kollinearität und Komplanarität mit Vektor- und Spatprodukt

    zur Aufgabe

Lernziele

  • Du kennst die Bedeutung von “kollinear” und kannst in eigenen Worten beschreiben, was es für zwei Vektoren heisst, wenn sie kollinear sind.
  • Du kannst rechnerisch nachweisen, dass zwei oder mehr Vektoren miteinander kollinear sind (oder nicht)
  • Du kannst rechnerisch nachweisen, ob zwei oder mehr Punkte auf der gleichen Geraden im Raum liegen (oder nicht)

Mini-Test

Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.

Mitglied werden

Weitere Links

Arbeit (Physik): Hubarbeit

Arbeit (Physik)

Kollineare Punkte (Wikipedia)

Feedback

Post Feedback Form

Autor dieses Artikels:

David John Brunner

Lehrer für Physik und Mathematik | Mehr erfahren

Kontakt

publiziert:

überarbeitet:

publiziert:

überarbeitet:

Frage oder Kommentar?

Frage/Kommentar?

Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.

Schreibe einen Kommentar