Gleichung einer Ebene

Parameterform

Bei der Besprechung der Linearkombination haben wir festgestellt, dass ein Vektor mit durch eine Linearkombination von zwei Vektoren ausgedrückt werden kann. Wir hatten das folgende Beispiel gesehen:

\[ \begin{pmatrix} 3 \\ 2 \end{pmatrix} \;\; = \;\; 3 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} \]

\[ = 3 \cdot \vec{e_x} + 2 \cdot \vec{e_y} \]

Wir sehen dann, dass wir eigentlich jeden Punkt \(P(P_x,P_y)\) auf diese Art erreichen können:

\[ \overrightarrow{OP} = \begin{pmatrix} P_x \\ P_y \end{pmatrix} \;\; = \;\; P_x \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + P_y \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} \]

\[ = P_x \cdot \vec{e_x} + P_y \cdot \vec{e_y} \]

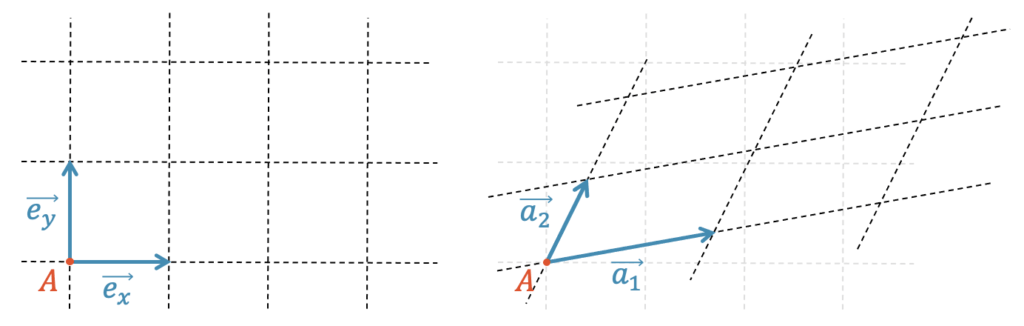
Wir können mit einer Linearkombination der beiden Vektoren \(\vec{e_x}\) und \(\vec{e_y}\) jeden Punkt \(P\) in der \(x,y\)-Ebene erreichen – oder – alle Punkte der ganzen \(x,y\)-Ebene, die durch die Vektoren \(\vec{e_x}\) und \(\vec{e_y}\) aufgespannt wird, kann mit einer Vektorgleichung beschrieben werden.

Es ist zu beachten, dass nicht nur die Einheitsvektoren \(\vec{e_x}\) und \(\vec{e_y}\) die \(x,y\)-Ebene aufspannen, sondern beliebige Paare von Vektoren, die in der \(x,y\)-Ebene und nicht kollinear sind. Wir können deshalb auch zwei Vektoren \(\vec{a_1}\) und \(\vec{a_2}\) nehmen und damit jeden Punkt der \(x,y\)-Ebene erreichen. Die Linearkombination ist eine andere, d.h. die “Koordinaten” im schiefwinkligen System von \(\vec{a_1}\) und \(\vec{a_2}\) sind anders, als die \(x-\) und \(y-\)Koordinaten.

Du erkennst sicher die Ähnlichkeit zur Gleichung einer Geraden \(g\):

\[ g \colon \;\; \overrightarrow{OP} \; = \; \overrightarrow{OA} + \lambda \cdot \vec{a} \]

Für die Ebene folgt entsprechend:

\[ E \colon \;\; \overrightarrow{OP} \; = \; \overrightarrow{OA} + \lambda_1 \cdot \vec{a_1} + \lambda_2 \cdot \vec{a_2} \]

Hier ist es aber wichtig, dass die beiden Richtungsvektoren \(\vec{a_1}\) und \(\vec{a_2}\) auch wirklich eine Ebene aufspannen. Das tun sie, wenn sie nicht kollinear sind, d.h. wir müssen sicherstellen, dass ihr Vektorprodukt nicht null ist:

\[ \vec{a_1} \times \vec{a_2} \; \neq \; \vec{0} \] 

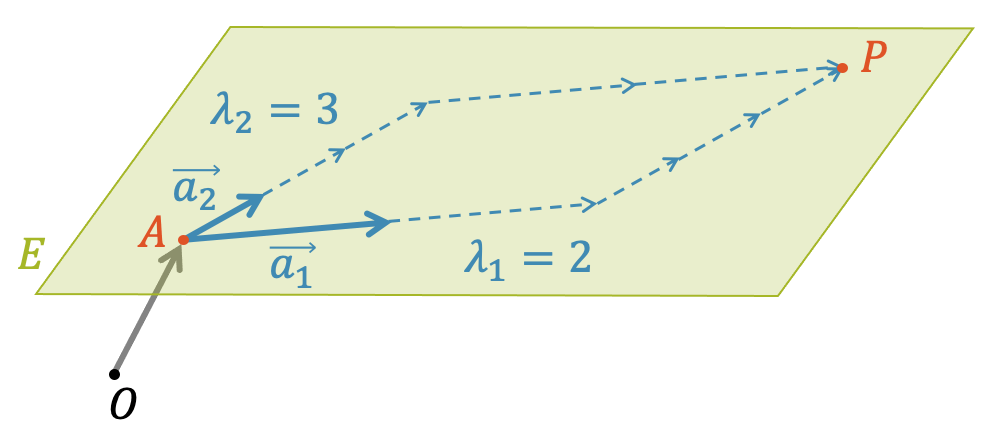
In der folgenden Grafik sehen wir, wie der Punkt \(P\) von \(A\) aus mit \(2 \cdot \vec{a_1}\) und \(3 \cdot \vec{a_2}\) erreicht wird. Jede erdenkliche Linearkombination mit den Parametern \(\lambda_1\) und \(\lambda_2\) wird jeden erdenklichen Punkt auf der Ebene \(E\) erreichen. 

Beispiel

Finde die Parameter \(\lambda_1\) und \(\lambda_2\), mit welchen der Punkt \(P(-23,12,46)\) auf der Ebene, von \(A(1,0,-2)\) aus, erreicht wird.

\[ E: \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix} + \lambda_1 \cdot \begin{pmatrix} 2 \\ 4 \\ 16 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 10 \\ -4 \\ -16 \end{pmatrix} \]

---

Die Vektorgleichung entspricht einem Gleichungssystem mit drei Gleichungen und zwei Unbekannten \(\lambda_1\) und \(\lambda_2\):

\[ \begin{cases} \begin{array}{cc} 1 + \lambda_1 \cdot 2 + \lambda_2 \cdot 10 = -23 \quad (a) \\ 0 + \lambda_1 \cdot 4 + \lambda_2 \cdot (-4) = 12 \quad (b) \\ -2 + \lambda_1 \cdot 16 + \lambda_2 \cdot (-16) = 46 \quad (c) \\ \end{array} \end{cases} \]

Das Gleichungssystem ist überbestimmt. Es reicht, wenn wir nur zwei Gleichungen nehmen und die beiden Unbekannten \(\lambda_1\) und \(\lambda_2\) aus ihnen gewinnen. Danach müssen wir aber die dritte Gleichung zur Überprüfung heranziehen. Um die Unbekannte \(\lambda_1\) zu eliminieren, addieren wir das \((-2)\)-fache der Gleichung \((a)\) zur Gleichung \((b)\):

\[ \begin{cases} \begin{array}{rr} -2 – 4 \cdot \lambda_1 – 20 \cdot \lambda_2 = 46 \\ 0 + 4 \cdot \lambda_1 – 4 \cdot \lambda_2 = 12 \\ \hline -2 + 0 – 24 \cdot \lambda_2 = 58 \\ \end{array} \end{cases} \]

\[ -24 \cdot \lambda_2 = 60 \quad \rightarrow \quad \underline{\lambda_2 = -\frac{5}{2}} \]

Wir setzen dieses Ergebnis in die erste Gleichung ein:

\[ 1 + \lambda_1 \cdot 2 + \Big(-\frac{5}{2}\Big) \cdot 10 = -23 \quad \]

\[ 2 \cdot \lambda_1 – 24 = -23 \quad \rightarrow \quad \underline{\lambda_1 = \frac{1}{2}} \]

Jetzt überprüfen wir die dritte Gleichung indem wir die Werte für \(\lambda_1\) und \(\lambda_2\) einsetzen und schauen, ob die Gleichung erfüllt bleibt:

\[ -2 + \frac{1}{2} \cdot 16 + \Big(-\frac{5}{2}\Big) \cdot (-16) \stackrel{?}{=} 46 \]

Tatsächlich ist die linke Seite gleich der rechten Seite. Die Gleichung ist erfüllt und unsere Lösung ist in Ordnung:

\[ E: \quad \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix} + \frac{1}{2} \cdot \begin{pmatrix} 2 \\ 4 \\ 16 \end{pmatrix} + \Big(-\frac{5}{2}\Big) \cdot \begin{pmatrix} 10 \\ -4 \\ -16 \end{pmatrix} \]

\[ = \underline{\begin{pmatrix} -23 \\ 12 \\ 46 \end{pmatrix}} \]

Normalform

Bei der Diskussion der Gleichung einer Geraden hatten wir die Normalform kennengelernt. Wir hatten damals schon gesagt, dass im dreidimensionalen Raum ein Normalvektor eigentlich normal zu einer Ebene ist. Da wir damals eine Gerade beschreiben wollten, hatten wir uns auf den zweidimensionalen Raum beschränkt, so dass aus der Ebene eine Gerade wurde.

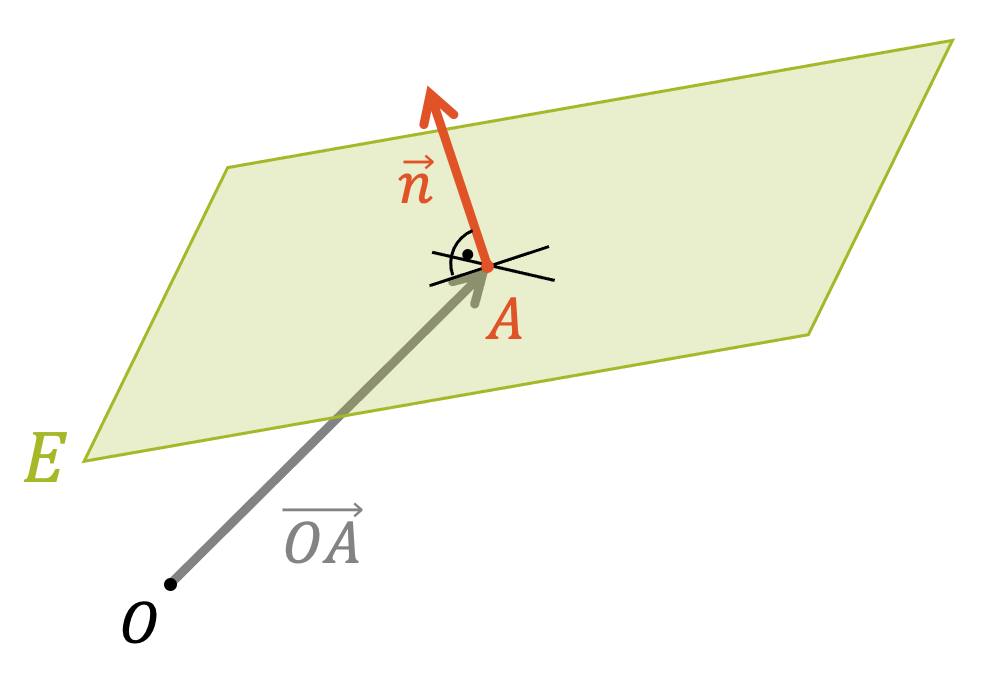
Jetzt können wir unser Wissen zur Normalform wieder einsetzen: Für die Beschreibung der Ausrichtung der Ebene reicht der Normalvektor \(\vec{n}\) aus. Wo diese ausgerichtete Ebene nun aber genau ist, wird durch einen verbindlichen Punkt \(A\) auf der Ebene bzw. durch ihren Ortsvektor, den Stützvektor \(\overrightarrow{OA}\) beschrieben.

Beispiel

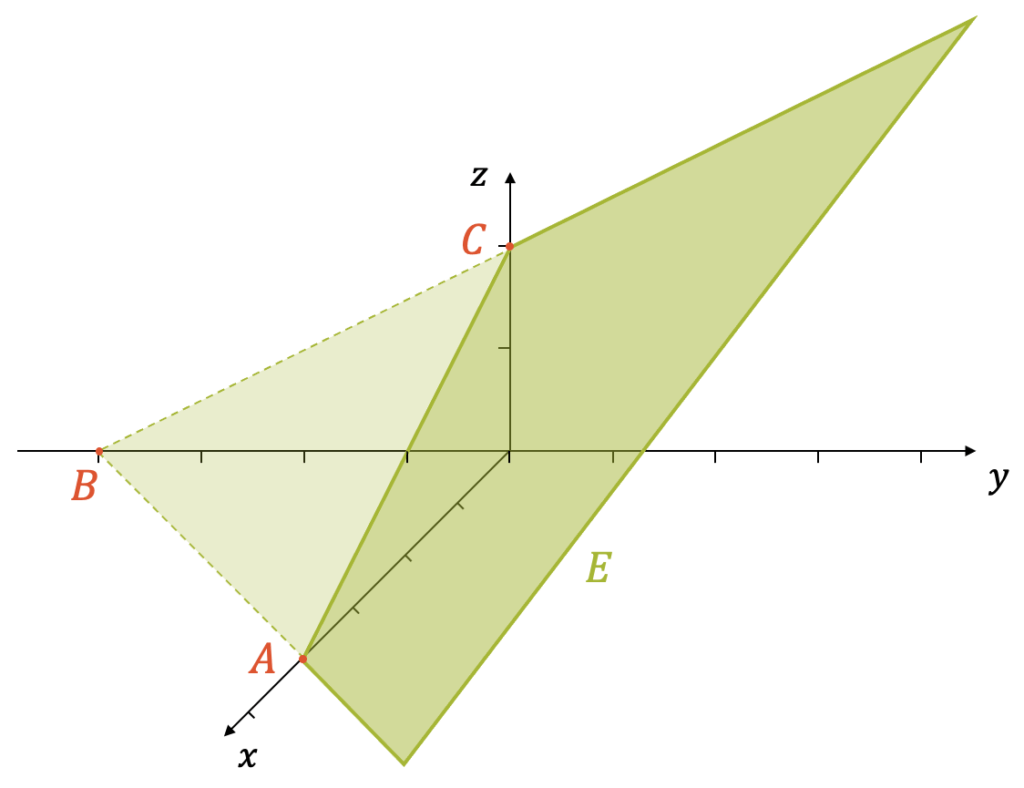
Die Ebene \(E\) enthält die Punkte \(A(2,0,-8)\), \(B(0,0,-12)\) und \(C(2,2,-2)\). Finde ihre Normalform.

---

Für die Normalform brauchen wir den Stützvektor zu einem Punkt auf \(E\) und den Normalvektor. Als Stützvektor brauchen wir einen Punkt auf der Ebene. Hier könnten wir jeden der drei Punkte wählen. Wir nehmen jetzt einfach den Punkt \(A\):

\[ \overrightarrow{OA} = \begin{pmatrix} 2 \\ 0 \\ -8 \end{pmatrix} \]

Den Normalvektor erhalten wir, wenn wir das Vektorprodukt der beiden Richtungsvektoren der Parameterform bilden. Die haben wir nicht, aber sobald wir zwei Punkte auf der Ebene miteinander verbinden, kriegen wir schnell einen Richtungsvektor, der in der Ebene liegt:

\[ \overrightarrow{AB} = \begin{pmatrix} 0 \\ 0 \\ -12 \end{pmatrix} – \begin{pmatrix} 2 \\ 0 \\ -8 \end{pmatrix} = \begin{pmatrix} -2 \\ 0 \\ -4 \end{pmatrix} \]

\[ \overrightarrow{AC} = \begin{pmatrix} 2 \\ 2 \\ -2 \end{pmatrix} – \begin{pmatrix} 2 \\ 0 \\ -8 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 6 \end{pmatrix} \]

Jetzt bilden wir das Vektorprodukt dieser beiden Richtungsvektoren:

\[ \overrightarrow{AB} \times \overrightarrow{AC} = \begin{pmatrix} -2 \\ 0 \\ -4 \end{pmatrix} \times \begin{pmatrix} 0 \\ 2 \\ 6 \end{pmatrix} = \begin{pmatrix} 8 \\ 12 \\ -4 \end{pmatrix} \]

Jetzt haben wir alles, was wir für die Normalform brauchen:

\[ E \colon \;\; \vec{n} \cdot \big( \overrightarrow{OP} – \overrightarrow{OA} \big) \]

\[ = \underline{\begin{pmatrix} 8 \\ 12 \\ -4 \end{pmatrix} \cdot \begin{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} – \begin{pmatrix} 2 \\ 0 \\ -8 \end{pmatrix} \end{pmatrix} = 0} \]

Koordinatenform

Die Koordinatenform folgt direkt aus der Normalform. Wir müssen dazu einfach das Skalarprodukt der Normalform ausmultiplizieren:

\[ \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} \cdot \begin{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} – \begin{pmatrix} A_x \\ A_y \\ A_z \end{pmatrix} \end{pmatrix} \]

\[ = \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} \cdot \begin{pmatrix} x-A_x \\ y-A_y \\ z-A_z \end{pmatrix} = 0 \]

\[ \quad n_x \cdot (x – A_x) + n_y \cdot (y – A_y) + n_z \cdot (z – A_z) = 0 \]

\[ \quad n_x \cdot x + n_y \cdot y + n_z \cdot z – (n_x A_x + n_y A_y + n_z A_z) = 0 \]

Der Ausdruck in der Klammer wird als Zahl \(-d\) abgekürzt:

\[ \quad n_x \cdot x + n_y \cdot y + n_z \cdot z + d = 0 \]

Beispiel

Gegeben ist der Normalvektor \(\vec{n}\) einer Ebene \(E\), die auch den Punkt \(A(2,0,-8)\) umfasst. Finde die Normalform und die Koordinatenform für diese Ebene.

\[ \vec{n} = \begin{pmatrix} 2 \\ 3 \\ -1 \end{pmatrix} \]

---

Für die Normalform brauchen wir den Stützvektor zu einem Punkt auf \(E\) und den Normalvektor. Den Letzteren haben wir schon in der Aufgabenstellung erhalten. Zudem wissen wir, dass der Punkt \(A\) auf der Ebene ist, d.h. wir können seinen Ortsvektor \(\overrightarrow{OA}\) als Stützvektor nehmen. Die Normalform ist demnach:

\[ E \colon \;\; \vec{n} \cdot \big( \overrightarrow{OP} – \overrightarrow{OA} \big) \]

\[ = \underline{\begin{pmatrix} 2 \\ 3 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} – \begin{pmatrix} 2 \\ 0 \\ -8 \end{pmatrix} \end{pmatrix} = 0} \]

Für die Koordinatenform schreiben wir das Skalarprodukt der Normalform einfach aus:

\[ 2 \cdot \big(x-2\big) + 3 \cdot \big(y-0\big) + (-1) \cdot \big(z-(-8)\big) = 0 \]

\[ 2x – 4 + 3y – 0 – z -8 = 0 \]

So erhalten wir schliesslich die Koordinatenform der Ebene \(E\):

\[ E \colon \;\; \underline{2x + 3y – z = 12} \]

Beispiel

Bestimme die Achsabschnitte der Ebene \(E\) auf der \(x-\), \(y-\) und \(z-\)Achse und zeichne die Ebene \(E\) im dreidimensionalen Koordinatensystem.

\[ E \colon \;\; x – y + 2z – 4 = 0 \]

---

Auf der \(x\)-Achse gilt: \(y=0\) und \(z=0\). Da wir die \(x\)-Achse mit der Ebene schneiden, setzen wir sie gleich bzw. wir setzen \(y=0\) und \(z=0\) in die Ebenengleichung ein und erhalten:

\[ y=0, z=0 \quad \rightarrow \quad x – 0 + 2 \cdot 0 – 4 \]

\[ = 0 \quad \rightarrow \quad x=4 \quad \rightarrow \quad \underline{A(4,0,0)} \]

Die \(x\)-Achse wird im Punkt \(A(4,0,0)\) geschnitten. Analog erhalten wir die anderen Schnittpunkte:

\[ x=0, z=0 \quad \rightarrow \quad 0 – y + 2 \cdot 0 – 4 = 0 \]

\[ \rightarrow \quad y=(-4) \quad \rightarrow \quad \underline{B(0,-4,0)} \]

\[ x=0, y=0 \quad \rightarrow \quad 0 – 0 + 2 \cdot z – 4 = 0 \]

\[ \rightarrow \quad z=2 \quad \rightarrow \quad \underline{C(0,0,2)} \]