Unabhängigkeit

Unabhängige Ereignisse

Die  Unabhängigkeit von Ereignissen ist sehr wichtig in der Stochastik. Achtung! Nicht zu verwechseln mit der Unvereinbarkeit. Ereignisse sind für uns unabhängig, wenn die Wahrscheinlichkeit für das Eintreten des einen Ereignisses nicht vom Eintreten des anderen Ereignisses abhängt.

Die beiden Ereignisse “es regnet” und “ich werde nass” sind offensichtlich abhängig von einander. Ich kann auch nass werden, ohne dass es regnet oder umgekehrt, aber es gibt offensichtlich eine Verbindung und wenn es regnet, ist die Wahrscheinlichkeit nass zu werden, eine andere als wenn es nicht regnet.

Unabhängige Ereignisse sind z.B. “es regnet” und “ich würfle eine 6”. Der Würfel wird vom Regen (draussen) nicht beeinflusst und der Regen wird auch nicht von meinem Würfel beeinflusst. Dieses beiden Ereignisse sind deshalb unabhängig.

Beweis der Unabhängigkeit

Mit Hilfe der bedingten Wahrscheinlichkeit, können wir die stochastische Unabhägngigkeit besser verstehen. Wir schauen uns das an einem Beispiel an:

Beispiel

Die Wirksamkeit eines neuen Zusatzes für eine Gesichtscrème wurde getestet. 120 Personen nahmen am Test teil. Um den Placebo-Effekt zu berücksichtigen, wurden 24 Crèmes __ohne__ den Zusatz verteilt. Zwei Drittel der Probanden, die die Gesichtscrème \underline{mit} Zusatz erhielten, stellten eine positive Wirkung fest. 16 Personen stellten eine Wirkung fest, obwohl ihre Crème keinen Zusatz enthielt.

Beweise, dass der Zusatz keine Wirkung hat.

---

Als Erstes definieren wir die zwei Ereignisse:

• \(A\) = positive Wirkung festgestellt
• \(B\) = Crème enthält Zusatz

Wir stellen die Vierfeldertafel auf mit den Spalten \(A\) und \(\overline{A}\) und den Zeilen \(B\) und \(\overline{B}\) und einer Spalte bzw. Zeile für die Summen. Ganz unten rechts schreiben wir 120 ein, da das die Summe aller Versuche ist.

Die 24 Crèmes ohne Zusatz werden in der Zeile \(\overline{B}\) ganz rechts in der Summenspalte aufgeschrieben. Daraus folgt, dass es 96 Crèmes mit Zusatz gegeben hat.

Die dritte Angabe in der Aufgabenstellung gibt uns eine bedingte Wahrscheinlichkeit: Die Probanden stellten eine positive Wirkung (Ereignis \(A\)) und es waren zwei Drittel der Probanden, die \(B\) erhielten. Damit ist \(B\) die Vorbedingung.

\[ P(A|B) = \frac{2}{3} \]

In der Vierfeldertafel heisst das, dass die Anzahl im Feld \(A \cap B\) zwei Drittel der Summe in der Zeile \(B\) sein muss, also zwei Drittel von 96, was uns 64 gibt. In der Zeile \(B\) (mit Zusatz) waren 64 Probanden der 96 zufrieden (\(A\)).

Schliesslich nehmen wir die Angabe der 16 Probanden auf, die eine Wirkung feststellten, obwohl ihre Crème keinen Zusatz enthielt. Diese 16 schreiben wir in die Spalte \(A\) und in die Zeile \(\overline{B}\). Wir können jetzt die restlichen Zahlen berechnen und erhalten die komplette Vierfeldertafel:

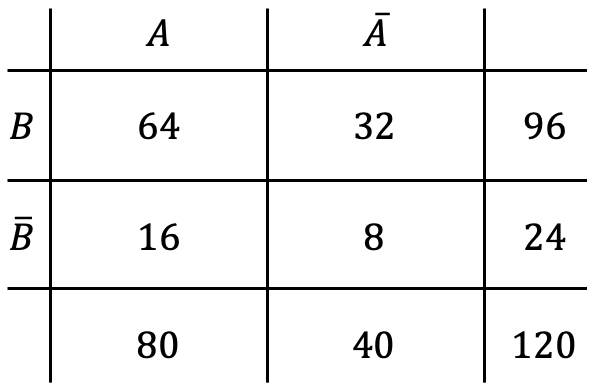
Um die Wirksamkeit des Zusatzes zu beweisen, berechnen wir zuerst die Wahrscheinlichkeit der Wirkung \(A\) im Bezug auf alle Versuche:

\[ P(A) = \frac{80}{120} = \frac{2}{3} \]

Dann berechnen wir die Wahrscheinlichkeit der Wirkung \(A\), unter Vorbedingung, dass der Zusatz beigegeben worden ist (\(B\)), d.h. Wirkung im Bezug auf alle Versuche mit Zusatz:

\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]

Die beiden Wahrscheinlichkeiten erhalten wir aus der Vierfeldertafel:

\[ P(A \cap B) = \frac{64}{120}, \quad \quad P(B)=\frac{96}{120} \]

Jetzt setzen wir diese beiden Werte ein und berechnen damit die bedingte Wahrscheinlichkeit:

\[ P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{\;\;\frac{64}{120}\;\;}{\frac{96}{120}} = \frac{64}{96} = \frac{2}{3} \]

Somit haben wir in diesem Beispiel:

\[ P(A|B) = P(A) \]

Wir kriegen die gleiche Wahrscheinlichkeit für eine Wirkung \(A\), ob wir nun Zusatz beimischen \(B\) oder nicht! Damit ist die Unwirksamkeit des Zusatzes bewiesen.