Bedingte Wahrscheinlichkeit

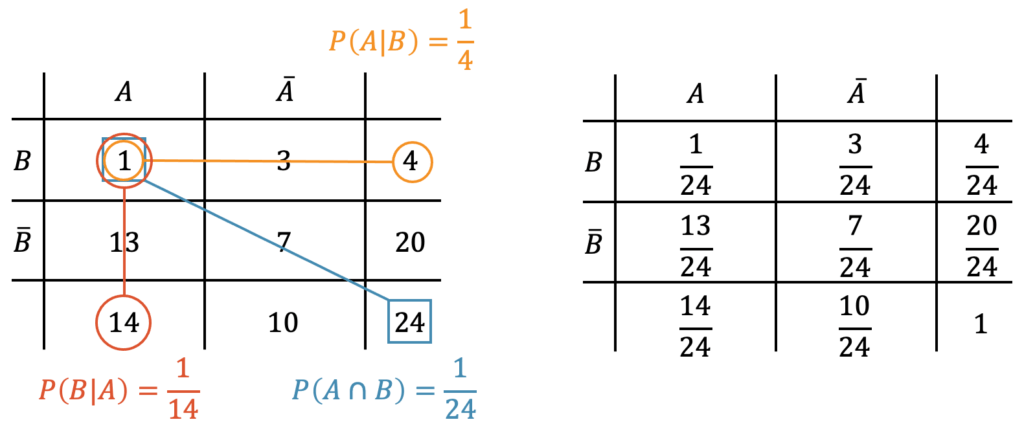
Wenn es unabhängige Ereignisse gibt, gibt es natürlich auch solche, die abhängig sind. Wir schauen uns das an einem Beispiel an. In einer Klasse mit 24 Schülerinnen und Schülern (14 Schülerinnen und 10 Schülern) hat es insgesamt 4 Brillenträger: 3 Schüler tragen eine Brille und 1 Schülerin. Wir fragen uns, wie gross ist die Wahrscheinlichkeit, dass beim zufälligen Ziehen einer Person aus der Klasse, es sich um die (einzige) Brillenträgerin handelt. 

Um uns hier einen Überblick zu verschaffen, tragen wir das in ein Diagramm ein und definieren die Ereignisse:

• \(A\) = Schülerin
• \(B\) = Brillenträger oder -trägerin

Die gesuchte Wahrscheinlichkeit ist die Wahrscheinlichkeit eine Schülerin zu ziehen und eine Person mit Brille, also die Schnittmenge von \(A\) und \(B\): \(P(A \cap B)\)

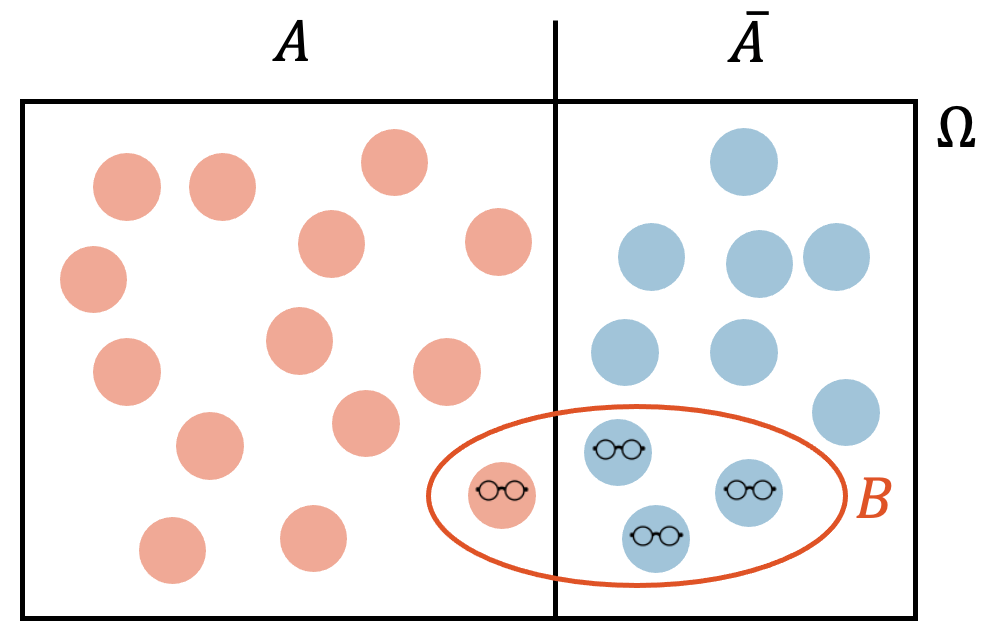
Wenn wir zufällig einen Schüler oder eine Schülerin aus dieser Klasse ziehen, dann ist es mit einer bestimmten Wahrscheinlichkeit eine Schülerin oder einen Schüler ohne Brille, oder eine Brillenträgerin oder ein Brillenträger. Um diese Wahrscheinlichkeiten in Zahlen zu übersetzen, zeichnen wir einen Ereignisbaum:

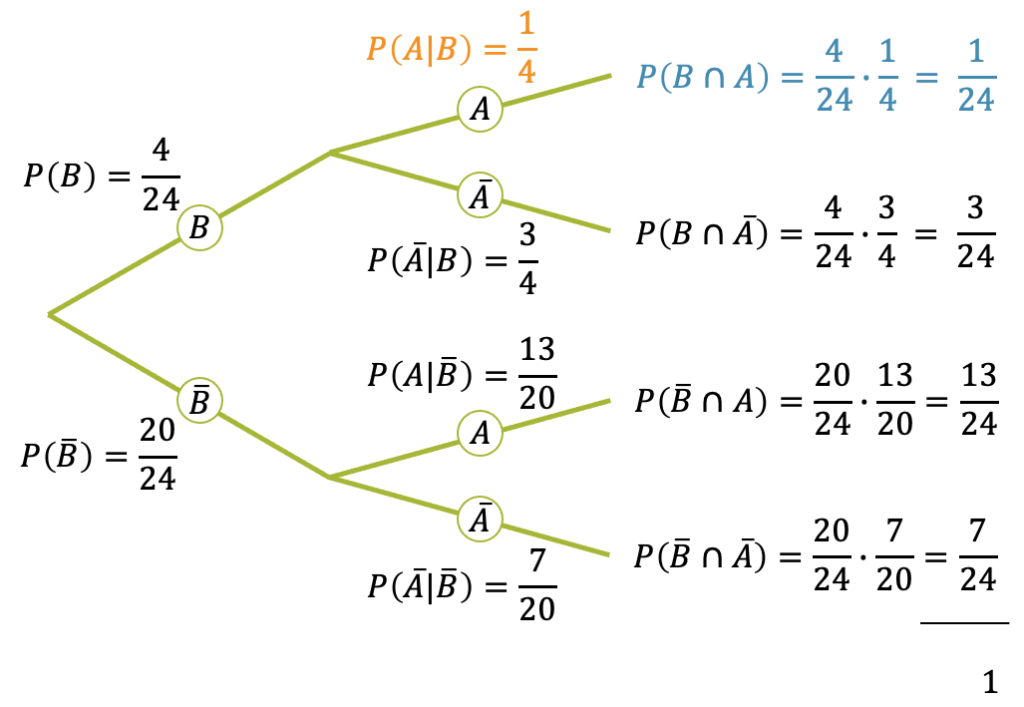
Schauen wir uns den obersten Ast genauer an: Die Wahrscheinlichkeit, dass wir die Brillenträgerin ziehen ist \(\frac{1}{24}\). Wir können es als mehrstufigen Prozess anschauen, in welchem zuerst eine Person mit Brille gezogen wird und dann aus den Brillenträgern die weibliche Brillenträgerin. Für den ersten Schritt haben wir die Wahrscheinlichkeit

\[ P(B) = \frac{4}{24} \]

Wir haben 24 Schülerinnen und Schüler und 4 davon tragen eine Brille. Jede Person kann gleich wahrscheinlich gezogen werden: \(\frac{1}{24}\). Die Wahrscheinlichkeit, eine Person mit Brille zu ziehen ist die Summe Wahrscheinlichkeiten der 4 Brillenträgerinnen und -träger und damit \(4 \cdot \frac{1}{24}\).

Nun kommt der zweite Schritt: Wie ist die Wahrscheinlichkeit, dass es sich um eine weibliche Person mit Brille handelt? In der ganzen Klasse hat es total 14 Mädchen. Die Wahrscheinlichkeit, dass wir aus der Klasse ein Mädchen ziehen, wäre \(\frac{14}{24}\). All die Schülerinnen und Schüler ohne Brille kommen aber nicht in Frage, denn wir haben ja im ersten Schritt den Ast für das Ereignis \(B\) gewählt und wissen, dass es sich um eine Person mit Brille handelt. Die Wahrscheinlichkeit, dass die Person mit Brille ein  Mädchen ist, ist deshalb eine sog. bedingte Wahrscheinlichkeit. Es ist die Wahrscheinlichkeit für das Ereignis \(A\) unter Bedingung, dass \(B\) erfüllt ist, d.h. die Wahrscheinlichkeit, dass die Person ein Mädchen ist, unter Bedingung dass sie eine Brille trägt. Mathematisch wird das so geschrieben:

\[ P(A | B) = \frac{1}{4} \]

Der senkrechte Strich steht für “unter der Bedingung, dass…”. Es ist die Wahrscheinlichkeit von Ereignis \(A\) unter der Bedingung, dass \(B\) erfüllt ist.

Jetzt können wir die Wahrscheinlichkeit, die Brillenträgerin aus der Klasse zu ziehen als das Produkt der Wahrscheinlichkeiten hinschreiben:

\[ P(A \cap B) = P(B) \cdot P(A | B) = \frac{4}{24} \cdot \frac{1}{4} = \frac{1}{24} \]

Mit einer einfachen algebraischen Umformung erhalten wir für die bedingte Wahrscheinlichkeit:

\[ P(A | B) = \frac{P(A \cap B)}{P(B)} \]

Die bedingte Wahrscheinlichkeit für das Ereignis \(A\) unter Bedingung, dass das Ereignis \(B\) erfüllt ist, wird aus der Wahrscheinlichkeit der Schnittmenge von \(A\) und \(B\) und aus der Wahrscheinlichkeit der Bedingung \(B\) errechnet:

\[ P(A | B) = \frac{P(A \cap B)}{P(B)} \]

Die bedingte Wahrscheinlichkeit \(P(A|B)\) ist die Wahrscheinlichkeit, dass \(A\) erfüllt ist, innerhalb aller Fälle, in denen \(B\) schon erfüllt ist. Im Gegensatz dazu ist \(P(A \cap B)\) die Wahrscheinlichkeit, dass \(A\) und \(B\) erfüllt sind, im Vergleich zu allen möglichen Fällen überhaupt.

Der Unterschied zwischen den beiden Wahrscheinlichkeiten \(P(A \cap B)\) und \(P(A | B)\) führt schnell zu einer Verwirrung. Bei der Wahrscheinlichkeit der Schnittmenge \(P(A \cap B)\) sagen wir “Die Wahrscheinlichkeit, dass \(A\) und \(B\) erfüllt sind”. Dabei beziehen wir uns auf die gesamte Menge möglicher Ereignisse.

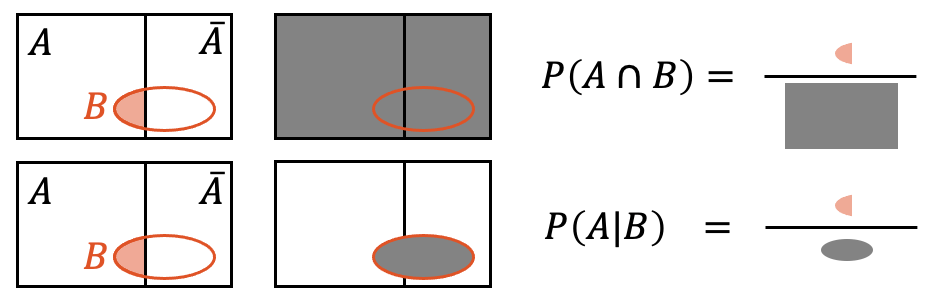
Bei der bedingten Wahrscheinlichkeit \(P(A | B)\) sagen wir im Prinzip das Gleiche: “Die Wahrscheinlichkeit, dass \(A\) unter Bedingung, dass \(B\) erfüllt ist”. Hier beziehen wir uns aber nicht auf alle möglichen Fälle, sondern ausschliesslich auf die Fälle innerhalb \(B\), denn \(B\) ist gesetzt!

Ist die bedingte Wahrscheinlichkeit von \(A\) unter Bedingung von \(B\) eventuell gleich der bedingten Wahrscheinlichkeit von \(B\) unter Bedingung von \(A\)? Nein, aber ganz abwegig ist die Frage nicht, denn die Schnittmenge ist kommutativ und wir können \(A\) mit \(B\) schneiden oder \(B\) mit \(A\) – es gibt keinen Unterschied:

\[ A \cap B = B \cap A \quad \rightarrow \quad P(A \cap B) = P(B \cap A) \]

Wir sehen aber aus der Definition der bedingten Wahrscheinlichkeit, dass der Nenner nicht der gleiche wäre, denn da steht die Wahrscheinlichkeit des Bedingungsereignisses:

\[ \frac{P(A \cap B)}{P(A)} = \;\; P(B | A) \;\; \neq \;\; P(A | B) \;\; = \frac{P(A \cap B)}{P(B)} \]

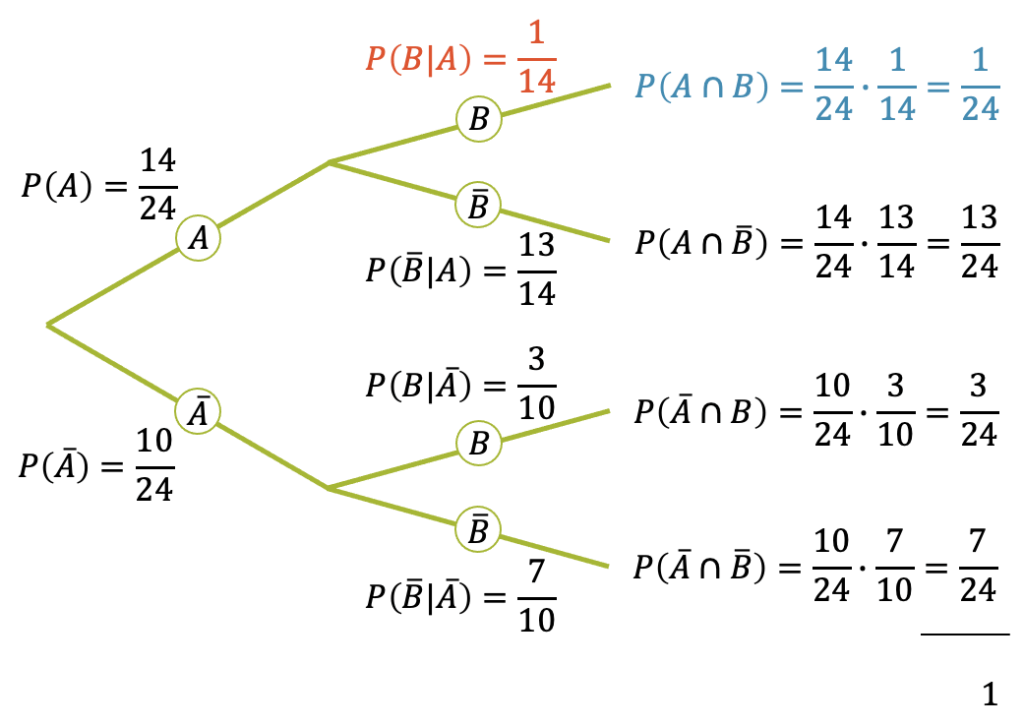
Den Unterschied zwischen \(P(A | B)\) und \(P(B | A)\) sehen wir auch, wenn wir den Ereignisbaum in der anderen Reihenfolge aufzeichnen. Die vier Wahrscheinlichkeiten, die wir mit den Pfadregeln erhalten, sind wieder die Gleichen. Die bedingte Wahrscheinlichkeit von \(B\) unter Bedingung von \(A\) ist tatsächlich anders:

\[ P(B | A) = \frac{1}{14} \]

Satz von Bayes

Der nach dem englischen Mathematiker Thomas Bayes benannte Satz folgt direkt aus der Definition der bedingten Wahrscheinlichkeit.

\[ P(A | B) = \frac{P(A \cap B)}{P(B)} \]

\[ P(B | A) = \frac{P(B \cap A)}{P(A)} \]

Die beiden Wahrscheinlichkeiten der Schnittmenge sind gleich, denn die Schnittmenge ist kommutativ. Somit können wir aus der zweiten Gleichung auch schreiben:

\[ P(B \cap A) = P(A \cap B) = P(B | A) \cdot P(A) \]

Das setzen wir in den Nenner der ersten Gleichung ein:

\[ P(A | B) = \frac{P(B | A) \cdot P(A)}{P(B)} = P(B | A) \cdot \frac{P(A)}{P(B)}\]

Der Satz von Bayes ermöglicht uns die Umrechnung von der einen bedingten Wahrscheinlichkeit in die andere:

\[ P(A | B) = P(B | A) \cdot \frac{P(A)}{P(B)}\]

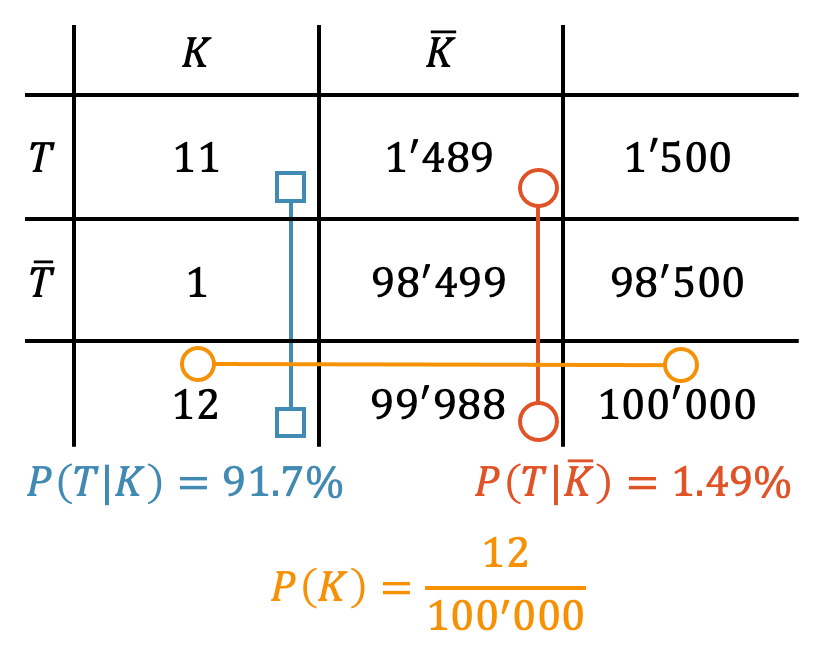
Einsatz von Vierfeldertafeln

Für bedingte Wahrscheinlichkeiten bietet sich die Darstellung mit sog. Vierfeldertafeln an, in welchen die Zahlen eingefüllt werden können. Es lohnt sich zudem die Summen der Zeilen bzw. Spalten ebenfalls aufzuführen. Für unser Beispiel haben wir die folgende Vierfeldertafel in welcher wir auch die bedingten Wahrscheinlichkeiten erkennen.