Für die meisten trigonometrischen Gleichungen brauchen wir einfach unseren Taschenrechner. Einfache Taschenrechner liefern uns im Normalfall nur ein Resultat, obwohl es eigentlich unendlich viele Lösungen gibt.
Was ist beispielsweise die Lösung der folgenden trigonometrischen Gleichung?
\[ \sin(x)=1 \]
Du erinnerst dich sicherlich, dass \(\sin(90°)=1\) und somit wäre die Lösung einfach
\[ x=90° \]
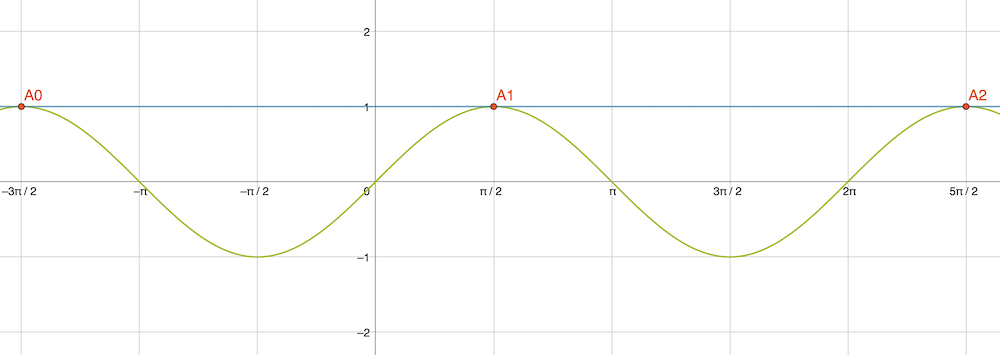
Das stimmt zwar, ist aber nur eine von unendlich vielen Lösungen, denn \(x\) = 450° oder \(x\) = -270° sind auch Lösungen. Das wird uns dann klar, wenn wir die Gleichung in einem Diagramm uns veranschaulichen. In der folgenden Abbildung wird der Funktionsgraph der Sinus-Funktion (grün) mit dem Funktionsgraphen der Gleichung \(y=1\) (blau) geschnitten. Wir sehen, dass die Gerade die Sinus-Kurve an den Maxima berührt und dass wir somit tatsächlich die erwähnten Lösungen haben. Jetzt ist auch klar, dass die Lösungen nach links und nach rechts in ihrer Anzahl unendlich sind.
Wenn du die folgende trigonometrische Gleichung nimmst
\[ \sin(x)= 0 \]
Dann haben wir natürlich auch wieder unendlich viele Lösungen. Es sind aber doppelt so viele, wie in der vorigen Gleichung. Aus dem Diagramm lesen wir ab:
\[ \boldsymbol{L}=\bigl\{ 0°, \pm 18 0°, \pm 36 0°, \pm 54 0°, … \bigr\} \]
Es sind Vielfache von 180°, d.h. wir könnten auch schreiben:
\[ x=\pm j \cdot 180° \quad \text{mit} \quad j \in \mathbb{N}_0 \]
Hier haben wir einen Zähler \(j\) eingeführt, der eine beliebige natürliche Zahl oder null sein kann.
Beispiel
Was sind die Lösungen der Gleichung \(\cos(x) = \frac{\sqrt{3}}{2}\) ?
Wir wissen, dass \(\cos(30°)=\frac{\sqrt{3}}{2}\). Das ist aber nur eine von unendlich vielen Lösungen. Wenn wir nämlich den Kosinus mit der grafischen Methode als \(y_1=\cos(x)\) aufzeichnen und gleichzeitig \(y_2=\frac{\sqrt{3}}{2}\), dann erhalten wir alle Schnittpunkte für die Lösungen, in welchen \(y_1 = y_2\) gilt.
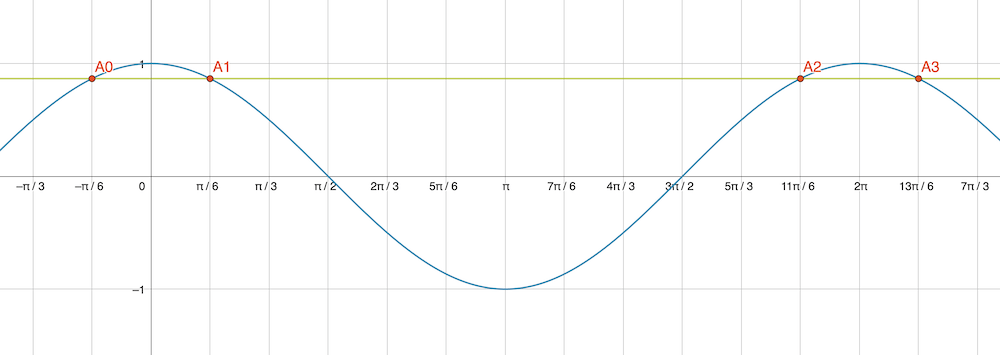
Dann gibt es einmal die Lösung \(x=30°\), sowie mit der Periode \(360°\) die weiteren Lösungen \(A_j\) mit ungeradem Index \(j\):
\[ x = 30° \pm j \cdot 360° \]
Es gibt auch die Lösung \(x=-30°\) und die weiteren Lösungen \(A_j\) mit geradem Index \(j\):
\[ x = -30° \pm j \cdot 360° \]
Transzendente Gleichungen
Transzendente Gleichungen können algebraisch nicht aufgelöst werden. Es gibt für sie nur noch numerische Verfahren oder grafische Lösungen. Wir schauen uns als Beispiel die folgende trigonometrische Gleichung an:
\[ \sin(x)=mx \]
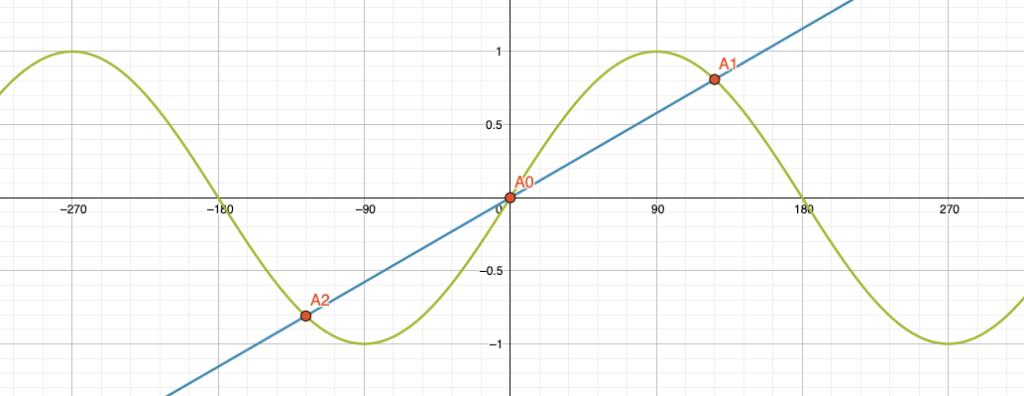
Wenn die Steigung der Geraden \(m\) genug gross ist, dann haben wir eine Lösung, nämlich \(x=0\), da wir nur einen Schnittpunkt haben. Wenn die Steigung aber klein ist, dann gibt es eine ungerade Anzahl von Lösungen. Die Lösung \(x=0\) einerseits und dann immer eine positive und eine negative Lösung für den Schnittpunkt der Geraden mit der Sinus-Kurve. Je flacher die blaue Gerade, desto öfters schneidet sie die Sinuskurve. Im folgenden Fall haben wir beispielsweise drei Lösungen:
\[ \boldsymbol{L}=\bigl\{ 0°, \pm 126° \bigr\} \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.