Wir spielen jetzt mit dem Winkel \(\alpha\) und lassen ihn bei null starten, erhöhen ihn immer mehr bis 90°, 180°, 270°, bis schliesslich 360°. Grössere Winkel brauchen wir uns nicht anzuschauen, denn von da an wiederholt sich die Sache nur, beispielsweise sollten wir für \(\sin(450°)\) gleich viel kriegen, wie für \(\sin(360°+90°)=\sin(90°)\).
Wir stellen eine kleine Wertetabelle auf und schreiben die \(y\)-Koordinate des Punkts A als Funktionswert der Sinus-Funktion auf:
| \(\alpha\) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| \(y=\sin(\alpha)\) | 0 | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | 1 | 0 | -1 | 0 |
Auf den ersten Blick sieht das doch etwas komisch aus. Die Sinus-Funktion startet bei null und endet wieder bei null. Bei 180°, also bei einer halben Umdrehung, erreicht sie wieder null. Sie wächst bis zum Maximalwert +1 und nimmt ab bis zum Minimalwert -1. Sie schwankt hin und her. Wenn die Sinus-Funktion aber die \(y\)-Koordinate unseres Punktes ist und wir diesen Punkt auf dem Einheitskreis rotieren lassen, dann muss ja die \(y\)-Koordinate immer wieder zu- und abnehmen und zwischen den Extremwerten +1 und -1 hin- und her schwingen. Tatsächlich wird die Sinus-Funktion in der Physik auch für die Beschreibung von Schwingungen benutzt.

Die Sinus-Funktion hat einen hübschen Verlauf (siehe Abbildung). Die wichtigsten Punkte, bei welchen die Funktion null oder den Maximal- bzw. Minimalwert \(\pm1\) erreicht, sollte man ebenfalls auswendig kennen. Hier hilft die Vorstellung der Sinus-Funktion als \(y\)-Koordinate des Punktes, der auf dem Einheitskreis rotiert.
Eigenschaften der Sinus-Funktion:
- startet mit null: \(\sin(0°)=0\)
- schwingt zwischen +1 (bei \(90°\)) und -1 (bei \(270°\))
- Null-Durchgänge bei \(0°\), \(180°\), \(360°\) etc.
- vollendet eine Periode bei \(360°\)
- ist eine ungerade Funktion: \(\sin(x)=-\sin(-x)\) (punktsymmetrisch)
Die Sinus-Funktion als Reihe
Wie \(\pi\) und \(e\) werden auch die Werte der trigonometrischen Funktionen mit Hilfe von Reihen berechnet. Wir schauen uns die Sinus-Funktion an. Sie kann als Reihe ausgedrückt werden, wobei nur die unendliche Summe der Sinus-Funktion gerecht wird. Brechen wir die Summe vorher ab, ist die Reihe nur eine Näherung.
\[ \sin(x) = \sum_{n=0}^{\infty}(-1)^n \frac{x^{2n+1}}{(2n+1)!} = \frac{x}{1!} – \frac{x^3}{3!} + \frac{x^5}{5!} – … \]
Nehmen wir ein Beispiel: Was ist der Wert von \(\sin(\frac{\pi}{4})\)? Es entspricht dem Sinus von 45° und der Taschenrechner spuckt uns \(\frac{1}{\sqrt{2}} = 0.7071068\) aus. Wenn wir nun die obige Reihe nehmen, sie aber mit dem Term mit der fünften Potenz abbrechen, so erhalten wir für die Sinus-Näherung:
\[ \frac{\frac{\pi}{4}}{1!} – \frac{\frac{\pi}{4}^3}{3!} + \frac{\frac{\pi}{4}^5}{5!} = 0.7071430 \]
Wir sehen, dass die fünfte Stelle nach dem Komma nicht mehr stimmt. Interessant für uns ist aber, dass viele mathematischen Grössen und Funktionen vom Taschenrechner nur approximiert werden, da er eigentlich nur addieren, subtrahieren, multiplizieren und dividieren kann. Mit Hilfe von Reihen kann er mit diesen Grundoperationen auch anderes. Je weiter er in der Reihe geht, desto genauer wird das Ergebnis. Meistens ist es für uns genug genau, aber es ist eigentlich nie ganz richtig.
Verlauf der Sinus-Funktion
Der Sinus ist ja eine Funktion, d.h. er ordnet einem Winkel \(\alpha\) einen Funktionswert zu:
\[ f: \quad \alpha \mapsto \sin(\alpha) \]
Um den Verlauf der Funktion kennenzulernen, lassen wir den Winkel \(\alpha\) schrittweise anwachsen und notieren die \(y\)-Koordinate unseres rotierenden Punktes A. Wir werden das mit 45°-Schritten tun, den für diese Winkel können wir die \(y\)-Koordinate im Einheitskreis einfach berechnen. Für alle anderen Winkel wäre das nicht mehr so einfach möglich.
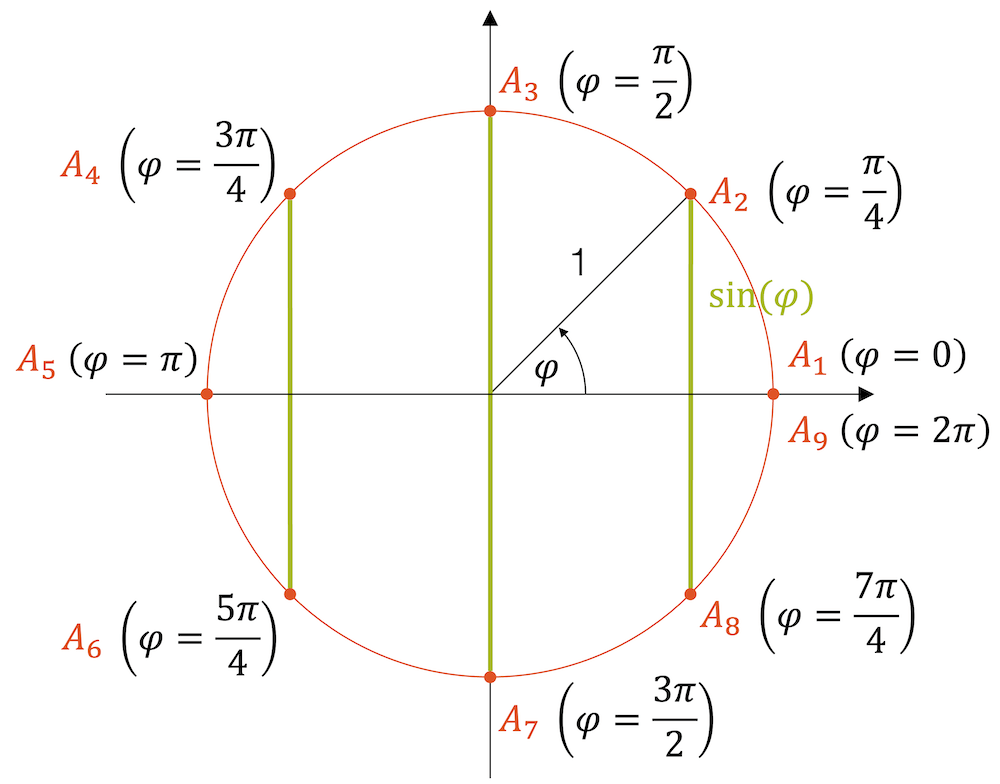
Für einen Winkel \(\alpha=0°\) haben wir noch \(\sin(0°)=0\). Für \(\alpha=45°\) haben ein rechtwinkliges Dreieck mit zwei gleich langen Katheten und einer Hypotenuse, die dem Radius des Einheitskreises (also 1) entspricht. Die \(y\)-Koordinate des Punktes A entspricht der Länge der Gegenkathete. Da beide Katheten aber gleich lang sind, gilt mit dem Pythagoras:
\[ y^2 + y^2 = 1^2 \]
und somit
\[ 2y^2 = 1 \]
und schliesslich
\[ y = \frac{1}{\sqrt{2}} \]
Der Wert der Sinus-Funktion ist damit: \(\sin(45°)=\frac{1}{\sqrt{2}}\).
Für den Winkel \(\alpha=90°\) erreichen wir den höchsten Punkt, d.h. \(\sin(90°)=0\). Dann geht die Sache wieder “bergab”. Für \(\alpha=135°\) ist der Winkel nicht mehr wirklich im Dreieck drin, aber die \(y\)-Koordinate unseres Punktes A ergibt wieder: \(\sin(135°)=\frac{1}{\sqrt{2}}\). Schliesslich landen wir mit \(\sin(180°)=0\) wieder bei null.
Mit noch grösser werdendem Winkel \(\alpha\) kriegen wir eine negative \(y\)-Koordinate. Wir füllen die restlichen Funktionswerte in eine Tabelle ein.
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
| \(\alpha\) | 0° | 45° | 90° | 135° | 180° | 225° | 270° | 315° | 360° | … |
| \(\sin(\alpha)\) | 0 | \(\frac{1}{\sqrt{2}}\) | 1 | \(\frac{1}{\sqrt{2}}\) | 0 | \(-\frac{1}{\sqrt{2}}\) | -1 | \(-\frac{1}{\sqrt{2}}\) | 0 | … |
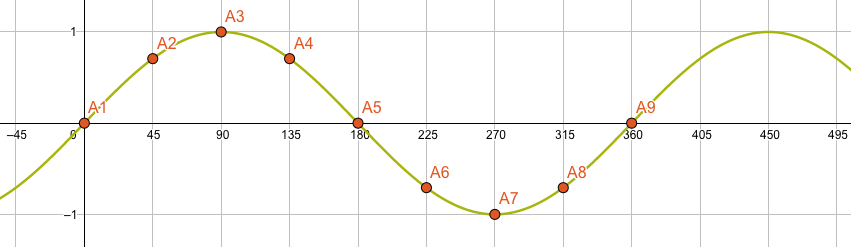
Jetzt kennen wir punktweise den Verlauf der Sinus-Funktion. In der nachfolgenden Grafik ist der Verlauf auch für die Zwischen werte gezeichnet. Es ist ein schönes Auf- und Ab zwischen den Schranken -1 und +1. Beachte, dass die Sinus-Funktion nach einer Umdrehung wieder von vorne beginnt, d.h. die Auf-Ab-Bewegung läuft unendlich weiter nach rechts, aber auch nach links.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.