Beziehungen zwischen trigonometrischen Funktionen

Sinus und Kosinus

Bei der Besprechung der Kosinus-Funktion ist uns schon aufgefallen, dass der Verlauf der Kosinus-Funktion gleich ist, wie der Verlauf der Sinus-Funktion, nur um 90° nach links versetzt. Wir können deshalb sagen, dass wir für eine andere \(x\)-Koordinate, die wir jetzt \(u\) nennen, aus dem Kosinus durchaus einen Sinus erhalten. Die y-Achse startet einfach 90° früher.

\[ \cos(x) \quad \stackrel{!}{=} \quad \sin(u) \]

Die Koordinate \(u\) ist so definiert, dass sie null ist, wenn die \(x\)-Koordinate noch -90° ist. Wir schreiben deshalb:

\[ u = x + 90° \]

Setzen wir \(x=-90°\) ein, erhalten wir tatsächlich \(u=0\). Somit ist die \(u\)-Koordinate gleich wie die \(x\)-Koordinate, nur um 90° nach links versetzt. Statt \(\sin(u)\) schreiben wir mit \(u = x + 90°\) eingesetzt:

\[ \cos(x) = \sin(u) = \sin(x + 90°) \]

Beispiel

Zeige am Beispiel des folgenden rechtwinkligen Dreiecks, dass \(\sin(\alpha) = \cos(\alpha – 90°)\)

---

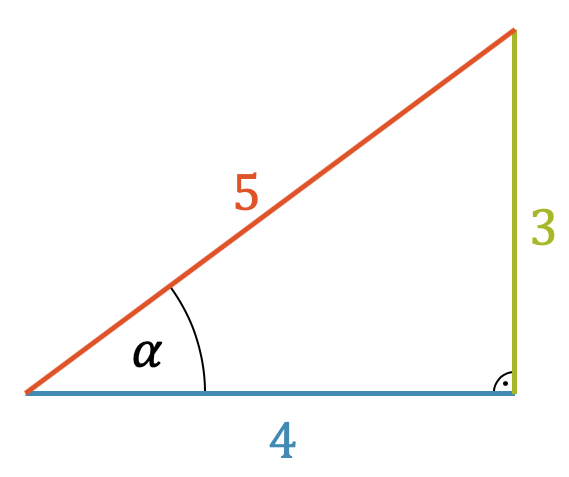
Der Sinus entspricht dem Bruch Gegenkathete zu Hypotenuse. In diesem Dreieck somit:

\[ \sin(\alpha) = \frac{3}{5} \]

Der Kosinus ist definiert als Ankathete zu Hypotenuse. Für den Winkel \(\alpha\) wäre das:

\[ \cos(\alpha) = \frac{4}{5} \]

Wir betrachten aber den anderen Winkel – nennen wir ihn einfach mal \(\beta\). Da die Winkelsumme im Dreieck \(180°\) beträgt, gilt für \(\beta\):

\[ \beta = 180° – (\alpha + 90°) = 90° – \alpha \]

Für den Winkel \(\beta\) ist der Bruch \(\frac{3}{5}\) Ankathete zu Hypotenuse, d.h. die Defintion des Kosinus’. Somit gilt:

\[ \cos(\beta) = \cos(90° – \alpha) = \frac{3}{5} \]

Damit folgt:

\[ \sin(\alpha) = \frac{3}{5} = \cos(90° – \alpha) \]

Jetzt ist das beim Kosinus noch nicht ganz, die Form, die wir haben wollten. Der Kosinus ist eine gerade Funktion, d.h. \(\cos(x)=\cos(-x)\). Wir können das Vorzeichen des Arguments einfach ändern, ohne dass sich etwas am Wert des Kosinus’ ändert. Damit erhalten wir, was wir zeigen wollten:

\[ \cos(90° – \alpha) = \cos\Big(-(90° – \alpha)\Big) = \cos(-90° + \alpha) = \underline{\cos(\alpha – 90°)} = \frac{3}{5} = \underline{\sin(\alpha)} \]

Tangens und Sinus / Kosinus

Bei der Besprechung des Einheitskreises haben wir gelernt, dass die Gegenkathete des Dreiecks dem Sinus entspricht, da die Hypotenuse eins ist. Die Ankathete entspricht dem Kosinus. Für den Tangens, das Verhältnis von Gegenkathete zu Ankathete, schreiben wir somit:

\[ \tan(x) = \frac{\sin(x)}{\cos(x)} \]