Arkusfunktionen

Arkusfunktionen als Umkehrfunktionen

Die Arkusfunktionen sind die Umkehrfunktionen der trigonometrischen Funktionen \(\sin(x)\), \(\cos(x)\) und \(\tan(x)\). Die Arkusfunktionen werden manchmal auch zyklometrische Funktionen oder inverse Winkelfunktionen genannt.

\[ y=\sin(x) \quad \leftrightarrow \quad x=\arcsin(y) \]

\[ y=\cos(x) \quad \leftrightarrow \quad x=\arccos(y) \]

\[ y=\tan(x) \quad \leftrightarrow \quad x=\arctan(y) \]

Im englischsprachigen Raum, aber auch auf den Tastaturen der meisten Taschenrechner, wird fast immer die Schreibweise mit dem Exponenten −1 verwendet. Dabei ist nicht die Potenz oder der Kehrwert, sondern die Umkehrfunktion der geschriebenen trigonometrischen Funktion gemeint:

\[ f(x)=\sin(x) \quad \leftrightarrow \quad f^{-1}(x) = \sin^{-1}(x) = \arcsin(x) \]

\[ f(x)=\cos(x) \quad \leftrightarrow \quad f^{-1}(x) = \cos^{-1}(x) = \arccos(x) \]

\[ f(x)=\tan(x) \quad \leftrightarrow \quad f^{-1}(x) = \tan^{-1}(x) = \arctan(x) \]

Arkussinus und Arkuskosinus

Um ein Gefühl für den Arkussinus zu entwickeln, schauen wir uns ein sehr einfaches Beispiel an:

\[ \sin\Big(\frac{\pi}{2}\Big) = 1 \]

Somit gilt mit der Umkehrfunktion:

\[ \arcsin(1) = \frac{\pi}{2} \]

Jetzt wissen wir aber, dass der Sinus eine periodische Funktion ist, d.h. für \(x=\frac{5\pi}{2}\) gilt ebenfalls:

\[ \sin\Big(\frac{5\pi}{2}\Big) = 1 \]

Beachte, dass wir jetzt nicht schliessen können, dass…

\[ \cancel{\arcsin(1) = \frac{5\pi}{2}} \]

Das geht nicht, denn dann würde die Arkussinus-Funktion dem Argument 1 einmal \(\pi/2\) und dann aber \(5\pi/2\) zuweisen. Das wäre keine eindeutige Zuweisung. Wir erinnern uns an die Theorie der Funktionen: Sie müssen eindeutig zuweisen!

Mit einem Trick kann auch eine periodische Funktion, wie die Sinusfunktion umgekehrt werden: Um auch für die Umkehrfunktion eine eindeutige Zuweisung hinzukriegen, wird die Funktion abgeschnitten. Es wird nicht die ganze Sinus-Funktion umgekehrt, sondern nur derjenige Teil, der streng monoton verläuft.

Die Sinus-Funktion läuft von \(x=-\frac{\pi}{2}\) bis \(x=+\frac{\pi}{2}\) einmal komplett von -1 bis +1 durch.

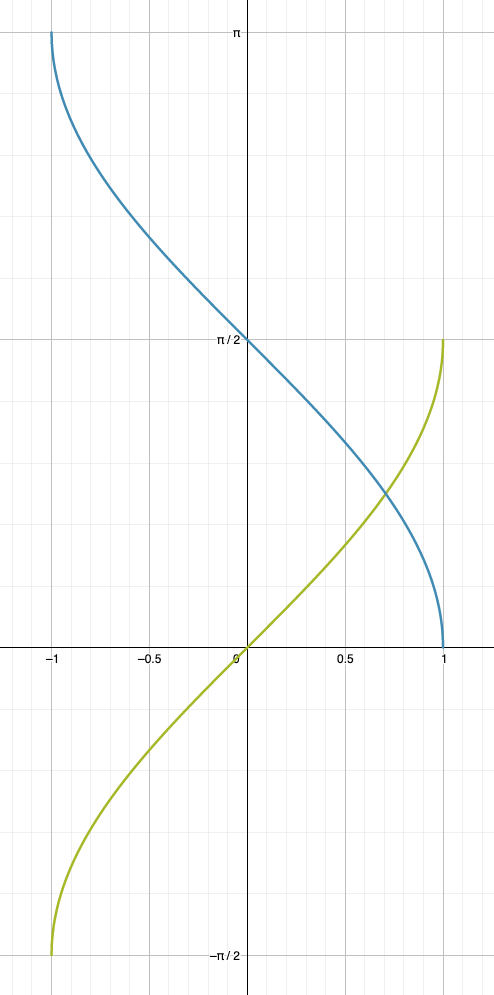
Die Arkussinus-Funktion ist dann die Umkehrfunktion für nur diesen beschränkten Bereich. Sie nimmt Werte auf von -1 bis +1 und liefert Winkel von \(x=-\frac{\pi}{2}\) bis \(x=+\frac{\pi}{2}\) (siehe oben).

Eigenschaften der Arkussinus-Funktion:

• steigt von \(-\frac{\pi}{2}\) bis \(+\frac{\pi}{2}\) für \(x=-1\) bis \(x=+1\) (streng monoton steigend)
• hat einen Null-Durchgang bei \(0\)
• Eingeschränkter Definitionsbereich: \(\boldsymbol{D} = \lbrack-1, +1\rbrack\)
• Eingeschränkter Wertebereich: \(\boldsymbol{W} = \lbrack-\frac{\pi}{2}, +\frac{\pi}{2}\rbrack\)
• ist eine ungerade Funktion: \(\arcsin(y)=-\arcsin(-y)\)

Für die Arkuskosinus-Funktion läuft das genau gleich. Sie nimmt ebenfalls Argumente aus dem Intervall \([-1,1]\) auf und gibt Funktionswerte nur im Intervall \([0,\pi]\) heraus.

Eigenschaften der Arkuskosinus-Funktion:

• sinkt von \(\pi\) bis \(0\) für \(x=-1\) bis \(x=+1\) (streng monoton fallend)
• Eingeschränkter Definitionsbereich: \(\boldsymbol{D} = \lbrack-1, +1\rbrack\)
• Eingeschränkter Wertebereich: \(\boldsymbol{W} = \lbrack 0, +\pi \rbrack\) (ist immer positiv)

Arkustangens

Für die Arkustangens-Funktion wurde die Tangens-Funktion auf den einen Ast beschränkt, der durch den Ursprung geht. Dieser eine Ast ist auf dem Definitionsbereich \(\lbrack -\frac{\pi}{2},+\frac{\pi}{2} \rbrack\) eingeschränkt.

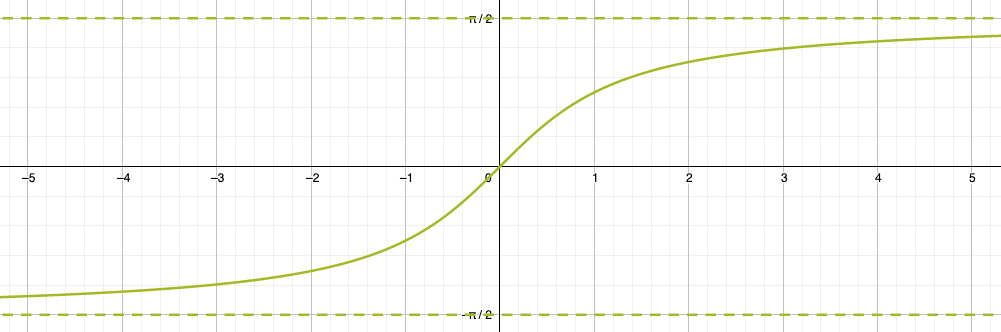
Von der Tangens-Funktion kennen wir noch z.B. diesen Punkt:

\[ \tan\Big(\frac{\pi}{4}\Big) = 1 \]

Somit erwarten wir für die Umkehrfunktion, dem Arkustangens:

\[ \arctan(1) = \frac{\pi}{4} \]

Eigenschaften der Arkustangens-Funktion:

• ist streng monoton steigend mit dem eingeschränkten Wertebereich: \(\boldsymbol{W} = \lbrack-\frac{\pi}{2}, +\frac{\pi}{2}\rbrack\)
• ist für alle reellen Werte von \(x\) definiert, d.h. \(\boldsymbol{D} = \mathbb{R}\)
• hat einen Null-Durchgang bei \(0\)
• ist eine ungerade Funktion: \(\arctan(y)=-\arctan(-y)\)