Gebrochen rationale Funktionen haben eine Funktionsgleichung als Bruch mit einem Polynom im Zähler und einem Polynom im Nenner. Die folgenden Funktionen sind Beispiele für gebrochenrationale Funktionen:
\[ y_1(x)=\frac{x^2+x-2}{x+1} \]
\[ y_2(x)=\frac{x-2}{x^2-4x+4} \]
\[ y_3(x)=\frac{1}{x^2} \]
Nullstellen
Gebrochenrationale Funktionen haben Nullstellen, wo ihr Zähler zu null wird. Wir müssen uns dazu das Polynom im Zähler anschauen und seine Nullstellen bestimmen. Dazu bringen wir das Zählerpolynom in die Produktform, d.h. zerlegen es in seine Faktoren und lesen an ihnen die Nullstellen ab.
Beispiel
Was sind die Nullstellen der folgenden Funktion?
\[ y_1(x)=\frac{x^2+x-2}{x+1} \]
Das Zählerpolynom kann in Produktform gebracht werden, z.B. durch quadratisches Ergänzen:
\[ y_1(x)=x^2+x-2 \;\; = \;\; x^2 + 2 \cdot \frac{1}{2} \cdot x -2 \;\; = \;\; \Bigl ( x^2 + 2 \cdot \frac{1}{2} \cdot x + \frac{1}{4} \Bigr ) – \frac{9}{4} \]
Wir fügen die binomische Formel ein und erhalten:
\[ y_1(x)=\Bigl ( x + \frac{1}{2} \Bigr )^2 – \frac{9}{4} \]
Jetzt setzen wir die Funktion gleich null, um die Nullstellen zu erhalten und ersetzen die \(\frac{9}{4}\) praktischerweise noch mit einem Quadratterm:
\[ \Bigl ( x + \frac{1}{2} \Bigr )^2 – \frac{9}{4} = 0 \]
\[ \Bigl ( x + \frac{1}{2} \Bigr )^2 = \Big(\frac{3}{2}\Big)^2 \]
Beachte, beim Wurzelziehen, dass wir rechts garantiert positiv sind (das Ergebnis einer Wurzel ist immer positiv), dass aber links der unbekannte Term in der Klammer auch negativ sein könnte.
\[ \pm (x + \frac{1}{2}) = \frac{3}{2} \]
Das gibt uns die beiden Lösungen:
\[ x=-\frac{1}{2} \pm \frac{3}{2} \]
bzw.
\[ \underline{\boldsymbol{L}=\bigl \{ -2, +1 \bigr \}} \]
Definitionsbereich
Sobald wir einen Bruch vor uns haben, sollten wir daran denken, dass er in bestimmten Fällen nicht definiert ist. Wenn der Nenner null beträgt, kann der Bruch nicht ausgerechnet werden. Er ist nicht definiert. Im vorigen Beispiel darf der Nenner \((x+1)\) nicht null sein. Das ist nie ein Problem, ausser wenn \(x=-1\). Dieser Wert ist schlicht nicht erlaubt. Für die Definitionsmenge von \(x\) schreiben wir deshalb: “\)x\) darf alle Werte annehmen, ausser \((-1)\)”” oder in mathematischer Schreibweise:
\[ \boldsymbol{L} = \mathbb{R} \; \backslash \; \bigl \{ -1 \bigr \} \]
Es ist wichtig, die Lösungen einer Gleichung oder die Lösungen für Nullstellen mit dem Definitionsbereich kurz abzugleichen. Lösungen, die nicht zum Definitionsbereich gehören, müssen wieder raus, da sie nicht erlaubt sind.
Beispiel
Was sind die Nullstellen der folgenden Funktion?
\[ y_2(x)=\frac{x-2}{x^2-4x+4} \]
Der Zähler ist schnell analysiert: \(x=2\) wäre eine Nullstelle. Jetzt schauen wir uns den Nenner an. Mit der binomischen Formel erhalten wir die Faktorzerlegung des Zählers:
\[ x^2-4x+4 = (x-2)^2 \]
Der Definitionsbereich schliesst damit den Wert \(x=2\) aus! Das war aber unsere Lösung für die Nullstelle. Somit ist die Antwort: Es gibt keine Nullstellen!
\[ \underline{\boldsymbol{L}=\bigl \{ \;\; \bigr \}} \]
Grad der gebrochenrationalen Funktion
Bei einem Polynom ist es relativ klar, wie wir den Grad bestimmen. Wir suchen die höchste Potenz und im Exponenten lesen wir den Grad des Polynoms ab. Bei einer gebrochenrationalen Funktion haben wir aber ein Zähler- und ein Nennerpolynom. Der Grad einer solchen Funktion wird deshalb aus beiden berechnet:
Der Grad einer gebrochenrationalen Funktion wird aus der Differenz des Grades des Zählerpolynoms und des Grades des Nennerpolynoms berechnet:
\[ Grad_{Funktion} = Grad_{Zaehler} – Grad_{Nenner} \]
Beispiel
Was ist der Grad der folgenden gebrochenrationalen Funktionen?
\[ y_1(x)=\frac{x^2+x-2}{x+1} \]
\[ y_2(x)=\frac{x-2}{x^2-4x+4} \]
\(y_1(x)\) hat einen Zähler vom Grad 2 und einen Nenner vom Grad 1. Somit ist der Grad der Funktion \(y_1(x)\): \(2-1=1\). Die Funktion \(y_1(x)\) verhält sich im Grossen und Ganzen wie eine lineare Funktion, d.h. sie verläuft von unten links nach oben rechts, wie \(y(x)=x\).
Allerdings hat sie eine Unstetigkeitsstelle bei \(x=-1\). Betrachte hierzu den Verlauf der grünen Funktion \(y_1(x)\).
\(y_2(x)\) hat einen Zähler vom Grad 1 und einen Nenner vom Grad 2. Somit ist der Grad der Funktion \(y_2(x)\): \(1-2=-1\). Die Funktion \(y_2(x)\) verhält sich im Grossen und Ganzen wie eine einfache Hyperbel, ähnlich wie \(\frac{1}{x}\), d.h. sie nimmt einen Wert von fast null an und fällt danach zu \(-\infty\) in einer Unstetigkeitsstelle, dann kommt der Verlauf von \(+\infty\) herunter und fällt asymptotisch wieder auf null herunter. Die Unstetigkeitsstelle liegt natürlich bei \(x=2\). Betrachte hierzu den Verlauf der blauen Funktion \(y_2(x)\).
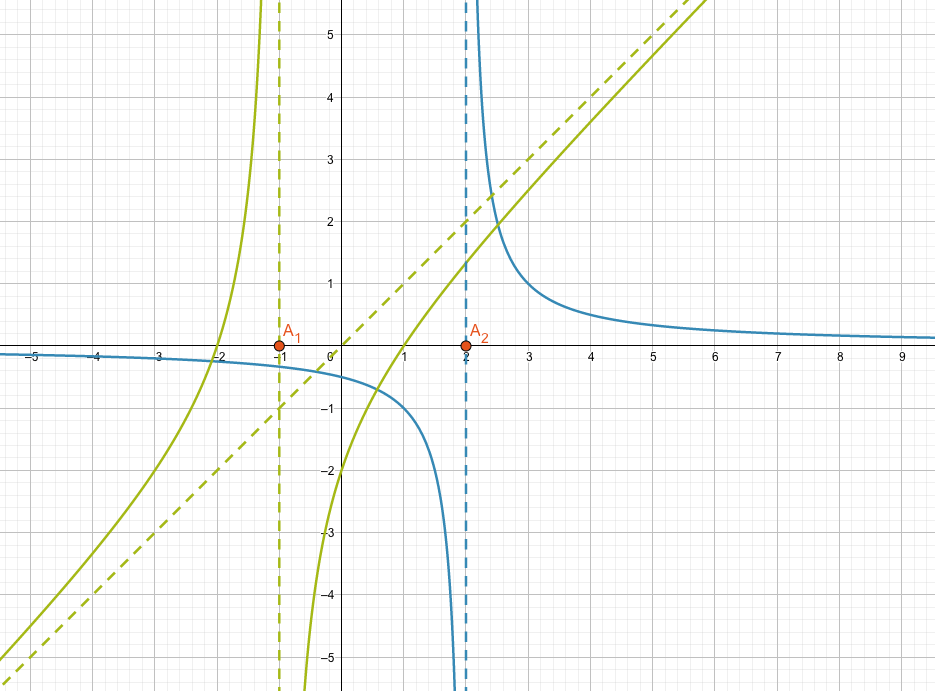
Der Verlauf einer gebrochenrationalen Funktion entspricht im Grossen und Ganzen dem der Grundfunktion vom Grad der gebrochenrationalen Funktion. Die Abweichungen treten in der Nähe der Unstetigkeitsstellen auf. In grossem Abstand von diesen Unstetigkeitsstellen, z.B. für \(x \rightarrow -\infty\) und \(x \rightarrow \infty\) nähert sich die Funktion immer mehr der Grundfunktion des Grades der gebrochenrationalen Funktion.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.