Lineare Gleichungen können grafisch mit Linien dargestellt werden. Wenn wir die grafische Methode benutzen, um Lösungen zu finden und die Linien gerade sind, so gibt es folgende Möglichkeiten: 1) Die beiden Linien schneiden sich in einem Punkt, der der Lösung entspricht. 2) Die beiden Linien sind parallel und schneiden sich deshalb nie. Es gibt keine Lösung.
Lineare Gleichungen sind Potenzgleichungen vom Grad 1, d.h. mit der ersten Potenz. Wenn die Unbekannte \(x\) ist, so enthält die lineare Gleichung ein \(x\), möglicherweise mit einem Faktor multipliziert.
Beispiele von linearen Gleichungen in \(x\):
\[ y=x \qquad y=3x+2 \qquad y=a^2x \]
\[ y=-x+1 \qquad x=3 \]
Beachte auch, dass die mittlere Gleichung \(y=a^2x\) linear in \(x\) ist, jedoch eine quadratische Gleichung in \(a\). Wenn \(a\) nur eine Zahl repräsentiert und \(x\) die Unbekannte ist, ist es eine lineare Gleichung.
Die Gleichung \(y=4\) würde grafisch zwar auch als gerade Linie dargestellt. Es ist aber keine lineare Gleichung in \(x\), sondern eine Potenzgleichung nullten Grades. Die höchste vorkommende \(x\)-Potenz ist \(x^0\), denn:
\[ y = 4 = 4 \cdot 1 = 4 \cdot x^0 \]
Beispiel
Löse die Gleichung \(3x+2=-x+1\)
Wir bringen die Unbekannte \(x\) auf eine Seite. Rechts können wir das \(-x\) eliminieren, indem wir \(x\) addieren. Wir erhalten:
\[ 4x+2=1 \]
Jetzt isolieren wir die Unbekannte auf der linken Seite, d.h. wir heben das +2 auf, indem wir von der Gleichung 2 subtrahieren:
\[ 4x=-1 \]
Jetzt dividieren wir die ganze Gleichung durch 4 und erhalten schliesslich:
\[\underline{x=-\frac{1}{4}}\]
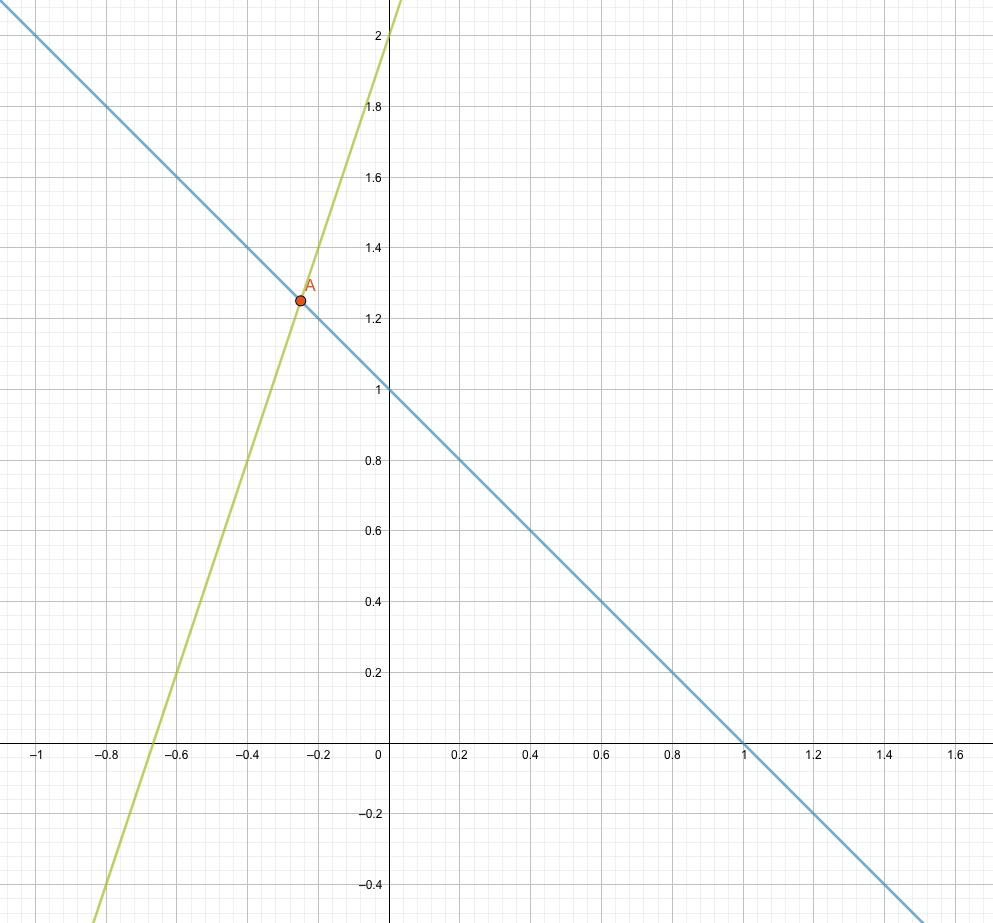
Lineare Gleichungen ergeben im Diagramm Geraden. Sie können null oder eine Lösung haben.
Beispiel
Der Vater von Tara ist 32 Jahre älter als sie. Vor zehn Jahren war er genau 5 mal älter als Tara. Wie alt ist Tara heute?
Sei \(v\) das Alter des Vaters, und \(t\) das Alter von Tara heute. Wir übersetzen die Aufgabenstellung in mathematische Gleichungen:
\[ v=t+32 \]
\[ (v-10) = 5 \cdot (t-10) \]
Wir haben zwei Gleichungen und zwei Unbekannte – soweit müsste alles klappen. Wir nehmen die zweite Gleichung und addieren 10 hinzu:
\[ v=5 \cdot (t-10) + 10 \]
Jetzt haben wir zwei lineare Gleichungen für \(v\), denn in der Unbekannten \(t\) kommt höchstens die 1. Potenz vor. Wir setzen die beiden Gleichungen gleich, weil sie das gleiche \(v\) beschreiben:
\[ t+32 = v=5 \cdot (t-10) + 10 \]
Jetzt subtrahieren wir 32 und multiplizieren rechts aus:
\[ t = 5t-50+10-32 \]
Wir bringen \(t\) auf eine Seite, indem wir \(5t\) subtrahieren. Die Zahlen werden miteinander verrechnet:
\[ -4t = -50+10-32 = -72 \]
Jetzt dividieren wir die Gleichung durch (-4) und erhalten die Lösung:
\[ \underline{t=18} \]
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.