Graphische Methode

Gleichungen und Unbekannte

Wie würdest du eine Gleichung definieren? Vermutlich etwas in der Art: Es gibt eine linke und einer rechte Seite. In der Mitte ist ein Gleichheitszeichen, das uns zeigt, dass beide Seiten den gleichen Wert haben.

\[ 1=1 \]

Das wäre eine Gleichung, aber sie bringt uns nichts, denn links und rechts steht einfach das Gleiche und das muss ja gleich sein. Im Gegensatz dazu ist die folgende Gleichung ein bisschen interessanter:

\[ x=1 \]

Jetzt wissen wir, dass die Unbekannte \(x\) einen Wert hat, nämlich 1. Die folgende Gleichung beinhaltet die gleiche Information, jedoch ist sie bereits weniger offensichtlich:

\[ x+1=2 \]

Sie sagt aus, dass wir die Unbekannte mit 1 addieren und dann den Wert 2 kriegen. Weil die Rechnung sehr einfach ist, wissen wir gleich, dass das die gleiche Aussage ist, wie \(x=1\). Gleichungen sind in der Regel aber viel komplexer, so dass wir den Wert von \(x\) nicht einfach “sehen”.

Wie steht es mit folgender Gleichung?

\[ y=x+1 \]

Wir erhalten die Information, dass die Unbekannte \(y\) gleich gross ist, wie \(x\) plus 1. Wir wissen, dass \(y>x\) oder dass die Differenz zwischen \(y\) und \(x\) genau 1 beträgt. Leider wissen wir aber nicht, wie viel \(x\) oder \(y\) tatsächlich betragen. Das Problem ist, dass wir eine Gleichung mit zwei Unbekannten haben. Die Grundregel lautet: Eine Gleichung kann Ihnen die Information für eine Unbekannte liefern. Für zwei Unbekannte brauchen wir zwei Gleichungen.

Eine zweite Gleichung könnte sein:

\[ y=4 \]

Damit löst sich alles: Wir haben \(y=4\) und \(y=x+1\), somit \(x=3\) und beide Unbekannten sind bestimmt. Nehmen wir jetzt aber an, dass wir stattdessen die folgende zweite Gleichung haben:

\[ y-1=x \]

Sie sieht anders aus als die erste Gleichung (\(y=x+1\)), ist aber eigentlich die gleiche Gleichung, nur in einer anderen Verpackung. Sie ist mit der ersten Gleichung äquivalent und liefert keine neue Information, die wir brauchen, um die Unbekannten zu bestimmen.

Lösungen als Schnittpunkte

Wir nehmen nochmals die beiden sehr einfachen Gleichungen von vorhin als Beispiel. Wir schreiben aber nur eine Gleichung auf:

\[ x+1 = 4 \]

Wir nehmen jetzt die linke Seite und stellen sie als Graphen im \(x,y\)-Koordinatensystem auf. Wir definieren deshalb:

\[ y_1 = x+1 \]

Für die rechte Seite machen wir das Gleiche:

\[ y_2 = 4 \]

Jetzt haben wir die Gleichung von oben reduziert auf:

\[ y_1 = y_2 \]

Jetzt nehmen wir ein \(x,y\)-Koordinatensystem und zeichnen die Punktscharen auf, die die beiden Gleichungen erfüllen. Betrachten wir zuerst die rechte Seite: Die \(x\)-Werte dürfen sein, was sie wollen. In jedem Fall ist \(y_2=4\). Wir erhalten \)\infty\)-lich viele Punkte, die ein beliebiges \(x\) und damit eine beliebige Position links oder rechts im Diagramm haben. Deren Höhe \(y\) im Diagramm ist aber immer konstant 4. Die Punkte bilden als Punktschar eine horizontale Linie auf der Höhe 4.

Für die linke Seite gilt: Die Höhe \(y_1\) ist einfach die Position \(x\) mit 1 dazu addiert. Mit grösserem \(x\) wird auch \(y_1\) grösser, d.h. je weiter rechts, desto weiter oben wir sind und umgekehrt, je weiter links, desto weiter unten. Wir erhalten eine gerade Linie, die von links unten nach rechts oben verläuft.

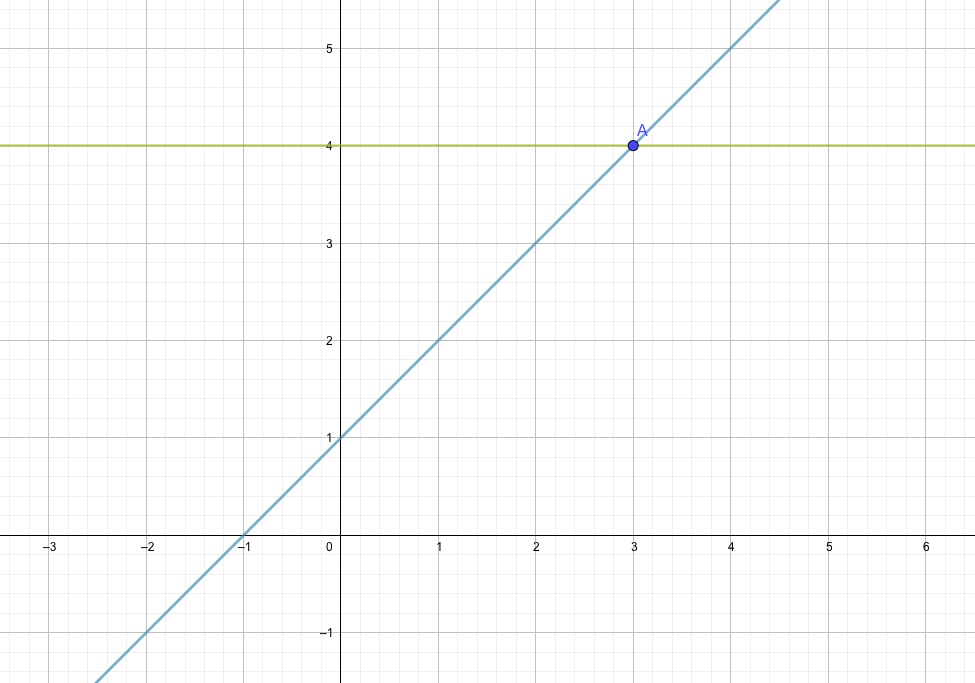
Im Diagramm sind beide Gleichungen eingezeichnet. Die blaue Linie entspricht \(y_1 = x+1\), die grüne Linie \(y_2 = 4\). Die Gleichung \(y_1 = y_2\) fordert jetzt, dass beide \(y\)-Werte gleich seien. Das ist in nur einem bestimmten Punkt erfüllt, dem Punkt Amit den Koordinaten \(A(3,4)\). Wichtig für uns ist die \(x\)-Koordinate. Sie ist die Lösung unserer Gleichung: \(x=3\). Wir haben so die Gleichung grafisch gelöst, mit der grafischen Methode eben.

Links vom Punkt A ist grün grösser als blau, d.h. die rechte Seite ist grösser als die linke Seite. Die Gleichung ist nicht erfüllt. Rechts vom Punkt A ist es gerade umgekehrt.

Ihnen mag diese Methode jetzt etwas aufwendig erscheinen. Für eine solch einfache Gleichung ist das sicherlich der Fall. Es gibt aber viel komplexere Gleichungen, die erst durch die grafische Methode besser verstanden werden können. Es gibt sogar Gleichungen, die mit Algebra nicht gelöst werden können, mit der grafischen Methode aber schon, wenn auch nicht ganz so exakt wie das die Algebra machen würde.

Wenn die beiden Linien sich nicht schneiden, dann wissen wir auch, dass die Gleichung keine Lösung hat.