Einfachlogarithmische Skala
Es wird dich überraschen, aber die menschlichen Sinnesorgane sind eigentlich logarithmisch! Wie ist das zu verstehen? Kannst du mit verbundenen Augen ein Gewicht von \(20\;\text{g}\) von einem Gewicht von \(60\;\text{g}\) unterscheiden? Sicher! Wie steht es mit zwei Gewichten von \(1020\;\text{g}\) und \(1060\;\text{g}\)? Vermutlich wird das schon recht schwierig! Der Unterschied ist aber in beiden Fällen \(40\;\text{g}\)!
Prozentual oder in Relation zum Gesamtgewicht ist der Unterschied aber gewaltig. Im ersten Fall vergleichen wir zwei Gewichte von 100% und 300% und im zweiten Fall von 100% und 104%.
Schauen wir uns ein zweites Beispiel an: Wir verdreifachen die Zahl \(\;1 \rightarrow 3 \; (\Delta = +2)\;\). Dann verdreifachen wir die Zahl \(\;30 \rightarrow 90 \; (\Delta = +60)\;\)
Im ersten Fall addieren wir nur 2, im zweiten Fall 60. Wenn wir das im gleichen Diagramm mit normaler linearer Skala darstellen, d.h. einer Skala mit regelmässigen Abständen (links), dann sehen wir die erste Änderung kaum (grün), währenddem die zweite Änderung (rot) optisch dominiert. Ist ja klar, das \(\Delta\) ist ja auch zwanzig mal grösser.
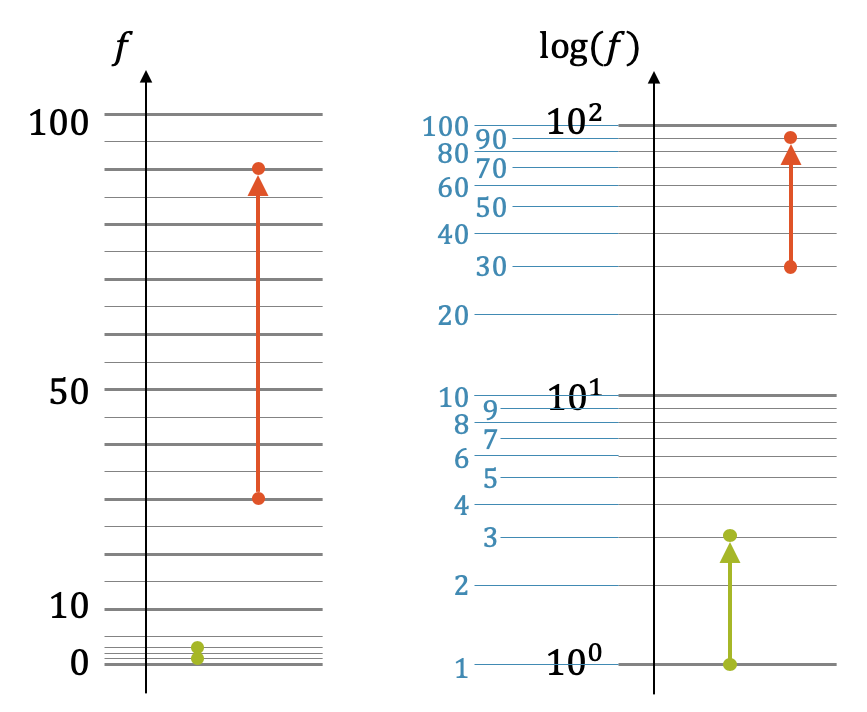
Wenn wir aber fair sein wollen und den Umstand unterstreichen möchten, dass in beiden Fällen die Zahl sich verdreifacht, die beiden Änderungen so gesehen eigentlich gleichwertig sind, dann wählen wir die einfachlogarithmische Skala (rechts). Diese Skala hat den Vorteil, dass die Umgebung von kleinen Zahlen vergrössert wird und die Umgebung von sehr grossen Zahlen verkleinert wird. Beispielsweise können wir auf diese Weise im gleichen Diagramm verschieden grossen Länder vergleichen, obwohl sie um Faktoren grösser oder kleiner sind.
Eine logarithmische Skala hat zwei wesentliche Vorteile:
- Kleine Zahleneffekte werden vergrössert, grosse Zahleneffekte werden verkleinert – Damit können verschieden grosse Effekte gleichzeitig im gleichen Diagramm dargestellt werden
- Prozentuale Veränderungen (bzw. Multiplikationen/Divisionen mit Faktoren) werden unabhängig von der Zahlenumgebung, gleich gross dargestellt, so dass die relative Veränderung vergleichbar wird (unabhängig von absoluten Grössen)
Einfachlogarithmische Skala für Exponentialfunktionen
Wenn wir beispielsweise den radioaktiven Zerfall untersuchen, dann kriegen wir eine exponentielle Zerfallsfunktion bzw. eine Abklingfunktion. Um die Sache etwas zu vereinfachen, nehmen wir an, dass der Grenzwert null ist.
\[ f(t) = a \cdot e^{-\frac{t}{\tau}} \]
Wir wissen wie der Verlauf dieser Funktion ausschaut: Sie fällt von oben links nach unten rechts und flacht nach rechts hin immer mehr ab. Wenn wir diese Funktion nicht kennen, aber Messpunkte haben, dann kriegen wir einen ungefähren Verlauf der Kurve. Das Problem ist aber: Wie sollen wir anhand dieser gekrümmten Kurve den Parameter \(\tau\) bestimmen? Die Verlängerung der Steigung im Anfangspunkt ist sehr ungenau und basiert auf vielleicht gerade mal drei Messpunkte.
Es gibt den viel besseren Trick mit der einfachlogarithmischen Skala. Wir setzen einfach \(f(t)\) in den natürlichen Logarithmus und erhalten:
\[ \ln\big(f(t)\big) = \ln\big(a \cdot e^{-\frac{t}{\tau}}\big) \]
\[ \ln\big(f(t)\big) = \ln(a) -\frac{t}{\tau} \]
Wir schreiben die rechte Seite etwas um:
\[ \ln\big(f(t)\big) = \Big( -\frac{1}{\tau} \Big) \cdot t + \ln(a) \]
Wenn du jetzt ganz genau hinschaust, solltest du die Struktur dieser Funktion erkennen. Sie ist von der Art:
\[ Y = m \cdot X + q \]
Es ist die Struktur einer linearen Funktion:
- Funktionswert: \(Y = \ln\big(f(t)\big)\)
- Steigung: \(m = \big(-\frac{1}{\tau}\big)\)
- Achsabschnitt: \(q = \ln(a)\)
Wir müssen nur die Messpunkte in ein einfachlogarithmisches Gitter eintragen und erhalten so eine lineare Funktion, deren Steigung und Achsabschnitt im Diagramm gut abgelesen werden kann. So bestimmen wir dann aus unseren Messpunkten die Parameter \(a\) und vor allem \(\tau\).
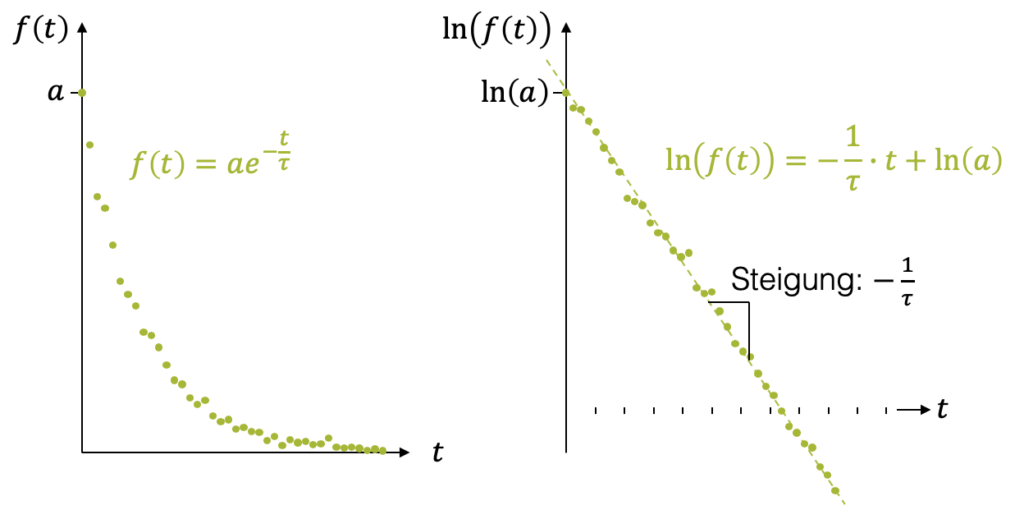
Beachte, dass die logarithmische Achse gegen unten immer näher zu null kommt, dieses aber nie erreicht. Streng genommen ist der Ursprung unendlich weit unten. Deshalb haben wir keine \(t\)-Achse gezeichnet, um diesen Umstand zu unterstreichen.
Beispiel
Im Jahr 1986 ereignete sich in Tschernobyl (ehemalige Sowjetunion, jetzt Ukraine) ein schwerer Reaktorunfall. Nachfolgend ging radioaktives Material, v.a. Cäsium (Cs-137), bis nach Westeuropa nieder.
Schätze anhand der roten Messkurve die Halbwertszeit von Cs-137 ab. Die Zeitachse für \(t\) hat eine Skala in Jahren. Bestimme wie viel Prozent des Cs-137 vom damaligen Reaktorunfall im Jahr 2020 noch vorhanden waren.
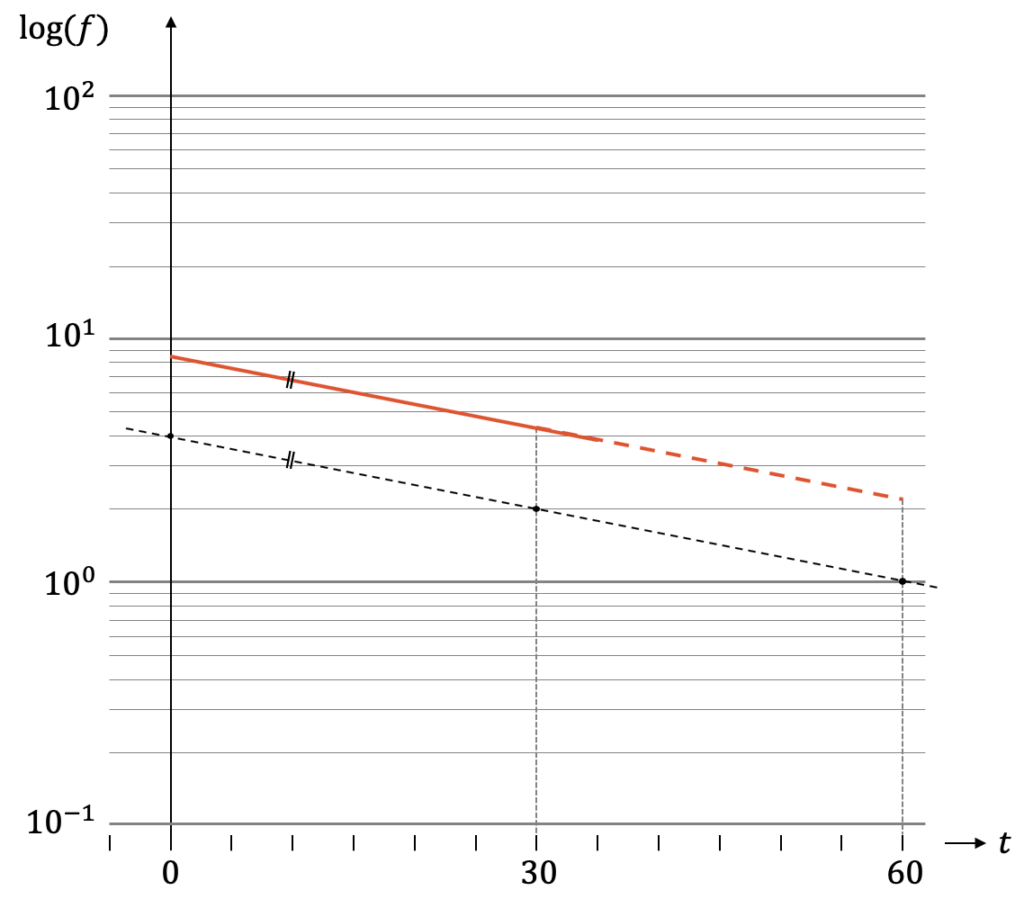
Der exponentielle Zerfall von CS-137 zeigt im einfachlogarithmischen Diagramm eine fallende Gerade. Wir wissen, dass aus der Abklingfunktion mit Grenzwert null, wir im einfachlogarithmischen Diagramm eine lineare Funktion erhalten:
\[ f(t) = a \cdot e^{-\frac{t}{\tau}} \quad \rightarrow \quad \ln\big(f(t)\big) = -\frac{1}{\tau} \cdot t + \ln(a) \]
Die Steigung unserer Geraden entspricht \(-\frac{1}{\tau}\), woraus wir \(\tau\) bestimmen können. Im Diagramm können wir die Gerade auch parallel verschieben, z.B. so, dass wir zum Start beim Wert 4 sind. Dieser halbiert sich zu 2 in der sog. Halbwertszeit. Warten wir den gleichen Zeitraum nochmals, halbiert sich der Funktionswert von 4 auf 2 usw. Aus dem Diagramm lesen wir ab, dass die Halbwertszeit offenbar 30 Jahre beträgt.
Wie viel im Jahr 2020 noch vorhanden ist, erhalten wir durch den Vergleich des Funktionswerts 34 Jahre nach der Katastrophe mit dem Wert zu Beginn, der unsere 100%-Referenz ist. Wir suchen den Wert von:
\[ \require{cancel} \frac{f(34)}{f(0)} = \frac{\cancel{a} \cdot e^{-\frac{34}{\tau}}}{\cancel{a} \cdot \cancel{e^{-\frac{0}{\tau}}}} = e^{-\frac{34}{\tau}} \]
Wir brauchen die Zeitkonstante \(\tau\). Das ist zwar eine charakteristische Zeit, jedoch nicht gleich der Halbwertszeit, denn nach der Zeit \(\tau\) haben wir noch \(\frac{1}{e} \approx 0.3679\), also schon weniger als die Hälfte. Demnach muss \(\tau > 30\) Jahre sein. Wir erhalten diese Grösse durch den Vergleich der Funktionswerte \(f(30)\) und \(f(0)\):
\[ \frac{f(30)}{f(0)} = e^{-\frac{30}{\tau}} \stackrel{!}{=} \frac{1}{2} \]
Wir wenden den natürlichen Logarithmus auf die ganze Gleichung an und erhalten:
\[ e^{-\frac{30}{\tau}} = \frac{1}{2} \]
\[ \ln\Big(e^{-\frac{30}{\tau}}\Big) = \ln\Big(\frac{1}{2}\Big) \]
\[ \require{cancel} -\frac{30}{\tau} = \cancel{\ln(1)} – \ln(2) \]
\[ \tau = \frac{30}{\ln(2)} = 43.28 \]
Jetzt setzen wir diesen Wert oben ein
\[ \frac{f(34)}{f(0)} = e^{-\frac{34}{\tau}} = e^{-\frac{34}{43.28}} = 0.46 = \underline{46\;\%} \]
Für den radioaktiven Zerfall wird die Abklingfunktion mit Grenzwert \(b=0\) benutzt:
\[ f(t) = a \cdot e^{-\frac{t}{\tau}} \]
Die Halbwertszeit \(t_{1/2}\) ist definiert als die Zeitspanne, nach welcher die Hälfte des Stoffs zerfallen sind:
\[ \frac{f(t_{1/2})}{f(0)} = e^{-\frac{t_{1/2}}{\tau}} = \frac{1}{2} \quad \rightarrow \quad t_{1/2} = \tau \cdot \ln(2) \]
Doppeltlogarithmische Skala
Die doppeltlogarithmische Skala ist nicht nur logarithmisch in vertikaler Richtung, sondern auch in horizontaler Richtung. Sie wird typischerweise eingesetzt, um Potenzfunktionen linear darzustellen.
Betrachten wir beispielsweise die folgende Funktion:
\[ f_1(x) = x^3 \]
Wenn wir die ganze Gleichung in den natürlichen Logarithmus setzen, erhalten wir:
\[ \ln\Big(f_1(x)\Big) = \ln\Big(x^3\Big) \]
\[ \ln\Big(f_1(x)\Big) = 3 \cdot \ln(x) \]
Das ist wieder die Struktur einer linearen Funktion mit Steigung 3. Wenn wir nämlich \(X=\ln(x)\) und \(Y=\ln\Big(f_1(x)\Big)\) setzen, erhalten wir:
\[ Y = 3 \cdot X \]
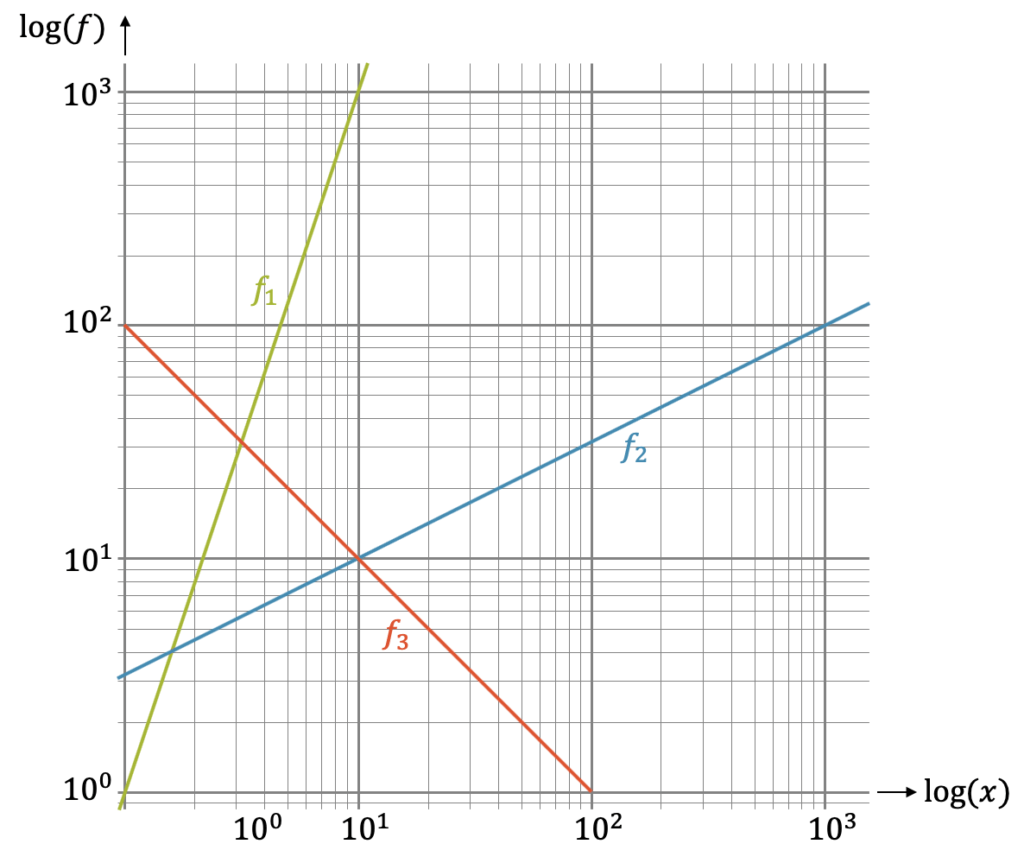
Wir können das schnell überprüfen. Die folgende Wertetabelle kann für die Funktion \(f_1(x)\) schnell aufgestellt werden:
| \(x\) | 1 | 2 | 4 | 8 | 10 |
| \(f_1(x)\) | 1 | 8 | 64 | 512 | 1000 |
Tragen wir diese Werte in das doppeltlogarithmische Diagramm ein, erhalten wir tatsächlich die grüne Gerade, wie in der folgenden Grafik.
Beispiel
Was ist die Funktionsgleichung der Funktion \(f_2(x)\), die in der obigen Grafik blau dargestellt ist?
Es ist eine Gerade und somit eine lineare Funktion, jedoch im doppeltlogarithmischen Diagramm. Die Steigung beträgt \(m=\frac{1}{2}\). Wir erkennen das daran, dass wir für zwei Quadrate nach rechts im doppeltlogarithmischen Gitter, wir ein Quadrat nach oben kommen. Folglich gibt uns dieses Steigungsdreieck die Steigung \(m=\frac{1}{2}\).
\[ Y = \frac{1}{2} \cdot X + q \]
Jetzt machen wir den umgekehrten Schritt von vorhin und ersetzen \(Y = \ln\big(f_2(x)\big)\) und \(X = \ln(x)\):
\[ \ln\big(f_2(x)\big) = \frac{1}{2} \cdot \ln(x) + q \]
\[ \ln\big(f_2(x)\big) = \ln\big(x^{1/2}\big) + q \]
\[ \ln\big(f_2(x)\big) = \ln\big((x^{1/2}\big) + \ln(e^q) \]
\[ \ln\big(f_2(x)\big) = \ln\big(x^{1/2} \cdot e^q\big) \]
\[ f_2(x) = (e^q) \cdot x^{1/2} \]
\[ f_2(x) = Q \cdot \sqrt{x} \]
Es ist die Quadratwurzel-Funktion! Das \(Q\) ist ein unbekannter Faktor, den wir aber schnell mit Hilfe eines Punkts bestimmt haben. Wir nehmen z.B. den Punkt \((10^1,10^1)\) aus dem Diagramm und setzen ein:
\[ 10^1 = Q \cdot \sqrt{10^1} \quad \rightarrow \quad Q = \frac{10}{\sqrt{10}} = \sqrt{10} \]
Daraus folgt die Gleichung für \(f_2(x)\):
\[ \underline{f_2(x) = \sqrt{10x}} \]
Im doppeltlogarithmischen Diagramm werden Potenzfunktionen zu Geraden. Deren Steigung \(m\) entspricht dem Exponenten:
- \(m > 1\;\;\) (klassische Potenzfunktion)
- \(0 < m < 1\;\;\) (Wurzelfunktion)
- \(m < 0\;\; \) (Hyperbelfunktion)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.