Das Wichtigste in Kürze

Das beschränkte Wachstum wird beschreiben durch den Verlauf der Sättigungsfunktion (Sättigungskurve) hat die folgende Funktionsgleichung:

\[ f(t) = b – a \cdot e^{-\frac{t}{\tau}} \]

Sie wird durch drei Parameter definiert:

    • Unterschied zum Grenzwert beim Start: \(a\)
    • Grenzwert für \(t \rightarrow \infty\): \(b\)
    • Zeitkonstante \(\tau\)

Die Sättigungsfunktion ist eine leichte Abwandlung der Abklingfunktion in dem Sinne, dass der Funktionswert anwächst. Obwohl es sich um eine Exponentialfunktion handelt, deren Funktionswert zunimmt, sprechen wir hier nicht von exponentiellem Wachstum. Es ist vielmehr ein Unterschied zwischen dem Anfangswert und dem Grenzwert, der mit der Zeit abklingt. So gesehen ist es eben eine abgewandelte Abklingfunktion.

Auch hier gibt es zahlreiche Beispiele aus Naturwissenschaft und Technik. Genau wie die heisse Kaffeetasse, deren Temperatur sich allmählich der Raumtemperatur annähert, würde ein kühles Getränk sich allmählich der Raumtemperatur annähern. Dieses Mal natürlich mit der Sättigungsfunktion. Das kühle Getränk nimmt Wärme von der Umgebung auf, bis es “gesättigt” ist und die gleiche Temperatur aufweist, wie die Umgebung.

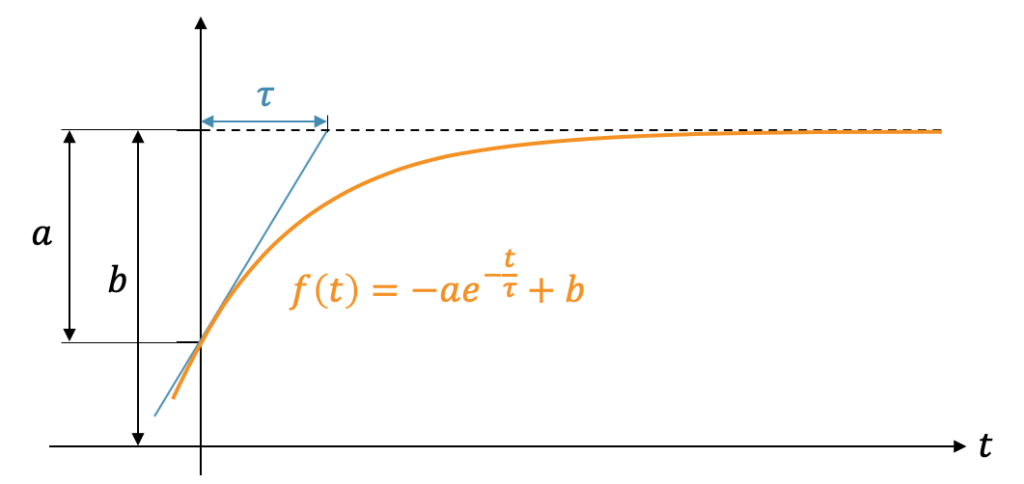
Beispiel: Berechnungsaufgabe mit Sättigungsfunktion

Bei der Mündung eines Stroms in das Meer mischen sich Süss- und Salzwasser. Das Meer hat die Salinität \(c_M=3.5\%\) (Massenkonzentration von gelösten Salzen) und das Flusswasser die viel kleinere Konzentration \(c_F=0.1\%\). Durch Diffusion und Mischströmungen steigt die Konzentration des Flusswassers in der Mündung an und wird durch die Sättigungsfunktion \(c(x)\) beschrieben:

\[ c(x) = c_M – (c_M – c_F) \cdot e^{-\frac{x}{\lambda}} \]

Bestimme die charakteristische Wegstrecke \(\lambda\), wenn 80% der Konzentrationsunterschiede nach 200 Metern verschwunden sind. Nach wie vielen Metern haben wir zu nur noch 1% Konzentrationsunterschied?

Gemäss Aufgabenstellung haben wir nach 200 Metern, d.h. für \(x=200\) eine Konzentration \(c(x)\), die nur noch 20% des ursprünglichen Konzentrationsunterschieds ausmacht. Mathematisch ausgedrückt heisst das:

\[ c(200) = c_M – (c_M – c_F) \cdot 0.2 \]

Andererseits besagt die Sättigungsfunktion an der Stelle \(x=200\):

\[ c(200) = c_M – (c_M – c_F) \cdot e^{-\frac{200}{\lambda}} \]

Wir setzen beides gleich:

\[ c_M – (c_M – c_F) \cdot 0.2 \;\;=\;\; c_M – (c_M – c_F) \cdot e^{-\frac{200}{\lambda}} \]

Beide Seiten sind gleich, wenn die Faktoren \(0.2\) und der exponentielle Teil gleich sind. Es folgt deshalb:

\[ 0.2 \;\;=\;\; e^{-\frac{200}{\lambda}} \]

Jetzt wenden wir den Trick an, indem wir die ganze Gleichung in den natürlichen Logarithmus setzen:

\[ \ln(0.2) \;\;=\;\; -\frac{200}{\lambda} \]

\[ \lambda \;\; = \;\; -\frac{200}{\ln(0.2)} \]

Wir erhalten so:

\[ \underline{\lambda = 124 \;\text{m}} \]

Wir erinnern uns, dass bei dieser charakteristischen Länge, rund zwei Drittel des Unterschieds verschwunden sind, weil hier nur noch der \(\frac{1}{e}\)-Teil des ursprünglichen Unterschieds übrig ist. Dieser Wert muss ja kleiner als 200 Metern sein, denn da haben wir ja schon 80% des Unterschieds verloren.

Für die zweite Frage setzen wir die Sättigungsfunktion mit unbekannter Länge \(x\) auf und setzen sie gleich der Konzentration des Meeres, abzüglich 1% des ursprünglichen Unterschieds zwischen Fluss und Meer.

\[ c_M – (c_M – c_F) \cdot e^{-\frac{x}{\lambda}} \;\; \stackrel{!}{=} \;\; c_M – 0.01 \cdot (c_M – c_F) \]

\[ e^{-\frac{x}{\lambda}} \;\; = \;\; 0.01 \]

\[ -\frac{x}{\lambda} \;\; = \;\; \ln(0.01) \]

\[ x = -\lambda \cdot \ln(0.01) \]

Durch Einsetzen des Werts für \(\lambda\) erhalten wir:

\[ \underline{x = 572\;\text{m}} \]

Autor dieses Artikels:

David John Brunner

Lehrer für Physik und Mathematik | Mehr erfahren

Kontakt

publiziert:

überarbeitet:

publiziert:

überarbeitet:

Frage oder Kommentar?

Frage/Kommentar?

Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.

Kommentar oder Frage schreiben