Potenzen mit einem positiven Exponenten, jedoch kleiner als eins, führen zu den Wurzelfunktionen. Wir betrachten hier nur die Wurzelfunktionen mit ganzzahligen Exponenten \(n\).
Unter einer Wurzelfunktion \(n\)-ter Ordnung verstehen wir eine Wurzel mit einem ganzzahligen, positiven Exponenten \(n\):
\[ f(x) = \sqrt[n]{x} = x^{\frac{1}{n}} \]
Für den Exponenten \(n\) gilt: \(n \in \mathbb{N}\) und \(n \geq 2\)
Wurzeln mit geraden Exponenten
Dieses Mal diskutieren wir zuerst die geraden Exponenten, denn die Quadratwurzel ist die “normalste” Wurzelfunktion, die wir am besten kennen. Ihre nächsten Verwandten sind die Wurzelfunktionen mit geraden Exponenten.
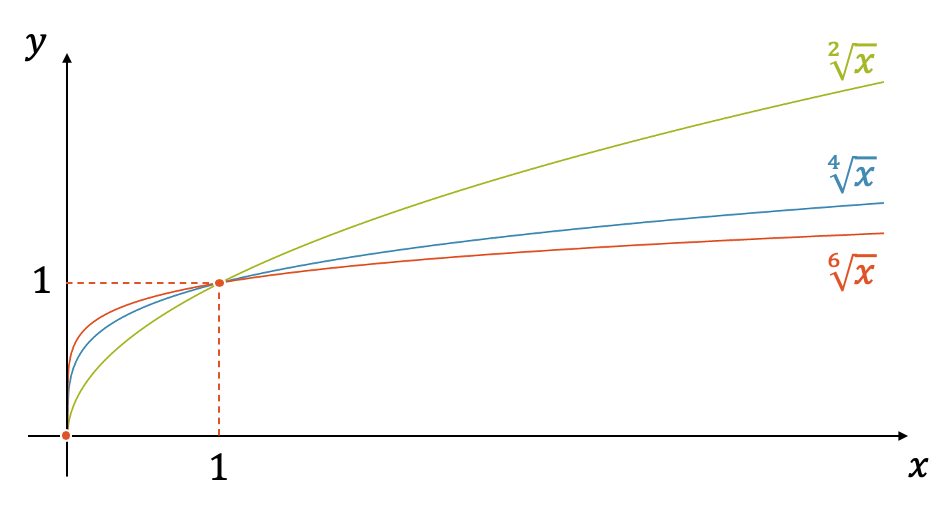
Nachfolgend sind ihre Eigenschaften aufgelistet:
- Die Funktionen verlaufen ausschliesslich im Quadranten oben rechts, d.h. für positive Werte von \(x\) und für ausschliesslich positive Funktionswerte
- Sie haben einen gemeinsamen Punkt: \((1,1)\), unabhängig von \(n\). In diesem Punkt wechseln die Verläufe von steil zu flach
- Links vom gemeinsamen Punkt sind die Funktionen mit grösserem \(n\) steiler und haben einen grösseren Funktionswert als solche mit kleinerem \(n\)
- Rechts vom gemeinsamen Punkt sind die Funktionen mit grösserem \(n\) flacher und haben einen kleineren Funktionswert als solche mit kleinerem \(n\)
- auch wenn der Verlauf nach rechts immer flacher wird, so nähert sich der Verlauf keinem Grenzwert an, sondern wächst ins Unendliche
- Die Funktion ist für negative \(x\) nicht definiert
- Der Ursprung ist allen Funktionen gemein
Wurzeln mit ungeraden Exponenten
Die Verläufe der Wurzelfunktionen mit ungeraden Exponenten sind für positive \(x\) analog zu denjenigen der geraden Exponenten. Allerdings sind die Wurzelfunktionen mit ungeraden Exponenten nicht nur auf positive Argumente \(x\) beschränkt, sondern sind auch für negative \(x\) definiert. Die Funktionswerte liegen alle im Quadranten unten links.
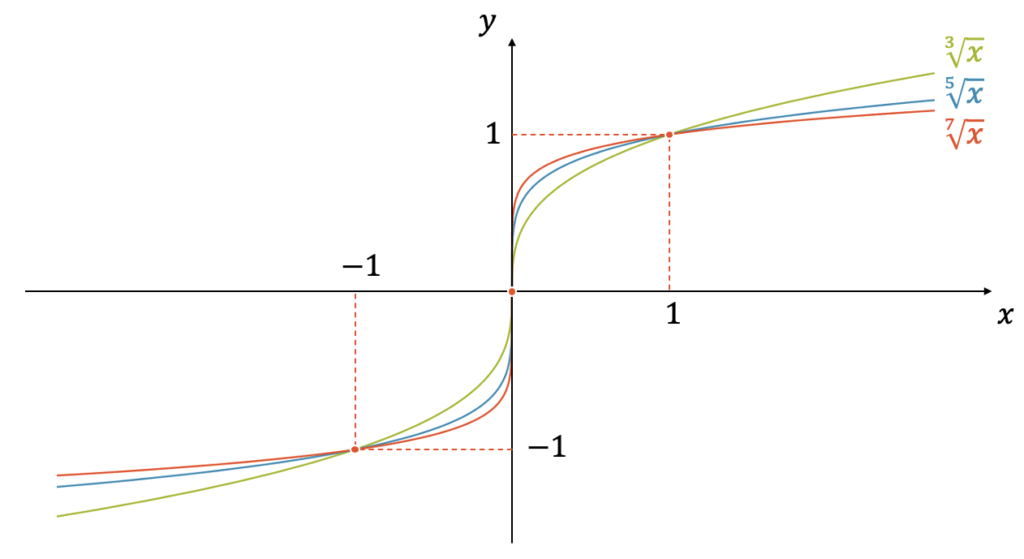
Nachfolgend sind ihre Eigenschaften aufgelistet:
- Die Funktionen verlaufen in den beiden oberen Quadranten unten links und oben rechts, wie ihre Verwandten, die Parabelfunktionen mit ungeraden Exponenten
- Ihre gemeinsamen Punkte sind: \((-1,-1)\) und \((1,1)\), unabhängig von \(n\)
- Je grösser \(n\), desto steiler verlaufen die Funktionen im steilen Bereich und desto kleiner sind die Funktionswerte im flachen Bereich
- Der Ursprung ist allen Funktionen gemein
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.