Wir kennen die linearen Gleichungen schon: Sie werden als Gerade dargestellt. Eine gerade Linie kann in einem beliebigen Winkel an einer beliebigen Stelle liegen. Wir schauen uns jetzt an, wie das mathematisch formuliert werden kann. Als Erstes geht es um den Winkel bzw. um die Steigung der Gerade.
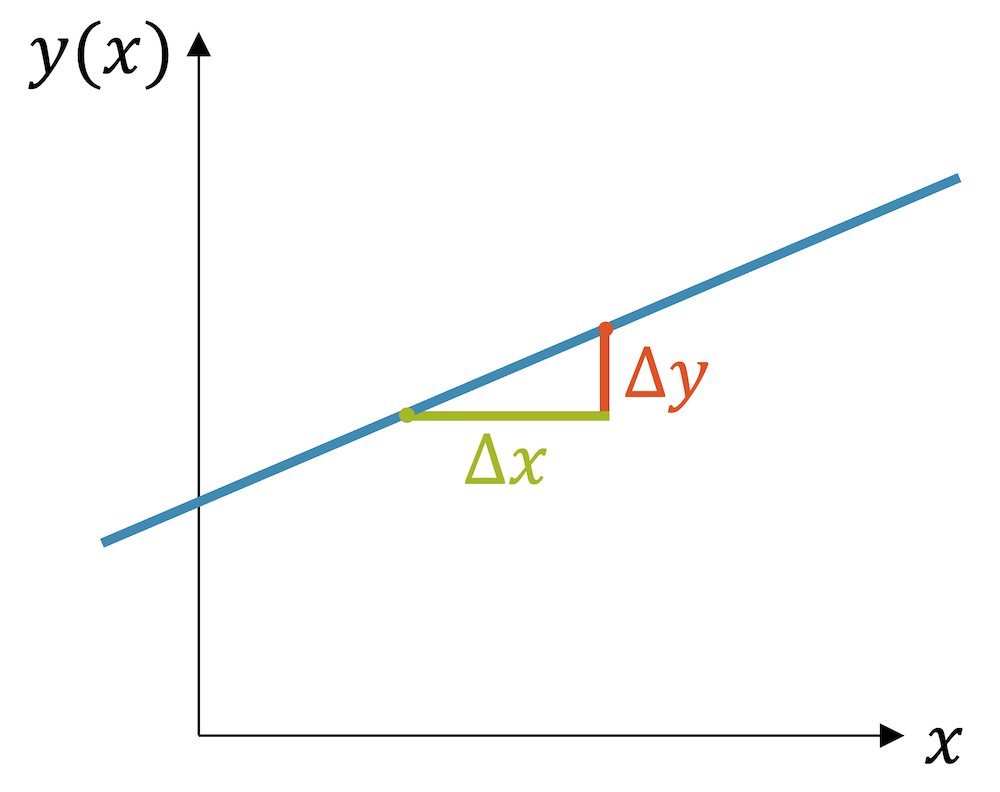
Die Steigung antwortet auf die Frage: Wie stark ändert sich der Funktionswert \(y\), wenn sich \(x\) verändert? Wir lassen also \(x\) um den Betrag \(\Delta x\) zunehmen. Die Funktion steigt dabei um \(\Delta y\). Bei gleichem \(\Delta x\) nimmt \(y\) bei einer steilen Geraden sehr stark zu, bei einer relativ flachen Geraden wenig, bei einer fallenden Geraden nimmt \(y\) sogar ab. Damit wäre \(\Delta y\) ein Mass für die Steigung.
Wenn wir aber ein doppelt so grosses \(\Delta x\) hätten, dann wäre auch \(\Delta y\) doppelt so gross, obwohl die Steigung gleich geblieben ist. Wir können deshalb nicht \(\Delta y\) alleine als Mass für die Steigung nehmen, sondern definieren die Steigung als die Veränderung \(\Delta y\) pro Veränderung \(\Delta x\).
Wenn wir zwei Punkte \(A\) und \(B\) auf der Geraden haben, dann erhalten wir \(\Delta x\) und \(\Delta y\) indem wir die Differenz der \(x\)- und \(y\)-Koordinaten der beiden Punkte bilden:
\[ \Delta x = x_B – x_A \]
\[ \Delta y = y_B – y_A \]
Die Steigung \(m\) ist definiert als:
\[ m=\frac{\Delta y}{\Delta x} = \frac{y_B – y_A}{x_B – x_A} \]
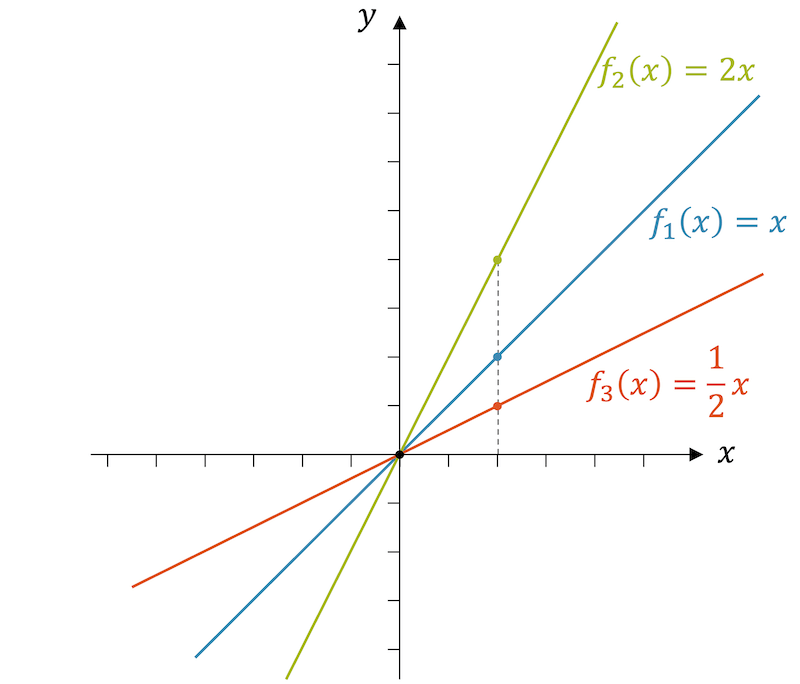
In der obigen Abbildung sind drei lineare Funktionen mit drei verschiedenen Steigungen eingezeichnet. Wir starten mit der blauen Grundgleichung für lineare Funktionen:
\[ y(x)=x \]
Um die Steigung \(m\) zu bestimmen, brauchen wir jetzt \(\Delta x\) und \(\Delta y\).
| \(x\) | 0 | 1 | 2 | \(\Delta x = 2\) |
| \(y(x)=x\) | 0 | 1 | 2 | \(\Delta y = 2\) |
Wir verändern \(x\) und schauen, wie stark \(y\) steigt. Wir schauen beispielsweise den Schritt von \(x=0\) zu \(x=2\) an:
\[ \Delta x = 2 \]
Die Änderung der Funktionswerte \(y\) beträgt ebenfalls 2, wie wir das aus der Wertetabelle ablesen können, somit ist
\[ m=\frac{\Delta y}{\Delta x}=\frac{2}{2}=1 \]
Die blaue Gerade hat die Steigung 1, weil die \(y\)-Werte gleich stark zunehmen, wie sich die \(x\)-Werte verändern.
Schauen wir uns die grüne Gerade an, so klettert sie von 0 auf 4, wenn wir \(x\) von 0 auf 2 wachsen lassen. Ihre Werte sind stets doppelt so gross wie diejenigen der blauen Gerade: Sie ist die mit dem Faktor 2 vertikal gestreckte Version der Grundgleichung \(y(x)=x\). Ihre Funktionsgleichung lautet deshalb:
\[ y(x)=2 \cdot x \]
Die rote Gerade erreicht bei einem \(\Delta x=2\), nur ein \(\Delta y=1\). Die Steigung der roten Gerade beträgt deshalb nur \(\frac{1}{2}\). Ihre Gleichung lautet:
\[ y(x)=\frac{1}{2} \cdot x \]
Wir verallgemeinern die Sache jetzt für eine beliebige Gerade mit der Steigung \(m\). Die Funktionsgleichung dieser Geraden ist:
\[ y(x)=m \cdot x \]
Parallel und senkrecht
Wenn zwei Geraden die gleiche Steigung haben, so sind sie zueinander parallel. Sie haben nicht unbedingt die gleichen Punkte, aber die Änderungspaare \(\Delta x\) und \(\Delta y\), die zu einander gehören, haben untereinander das gleiche Verhältnis und ergeben somit den gleichen Bruchwert \(m\).
Parallele Geraden haben die gleiche Steigung \(m\).
\[ m_1 = m_2 \qquad \Leftrightarrow \qquad g_1\;||\;g_2 \]
Wenn wir eine Gerade \(g_1\) mit Steigung \(m_1\) um 90° im Uhrzeigersinn drehen, so erhalten wir eine Gerade \(g_2\), die genau senkrecht auf der ersten Gerade steht. Aus dem \(\Delta x_1\) der ersten Gerade wird ein \(\Delta y_2\) der zweiten Gerade. Durch Drehung des \(\Delta y_1\) der ersten Gerade erhalten wir \(-\Delta x_2\) der zweiten Gerade:
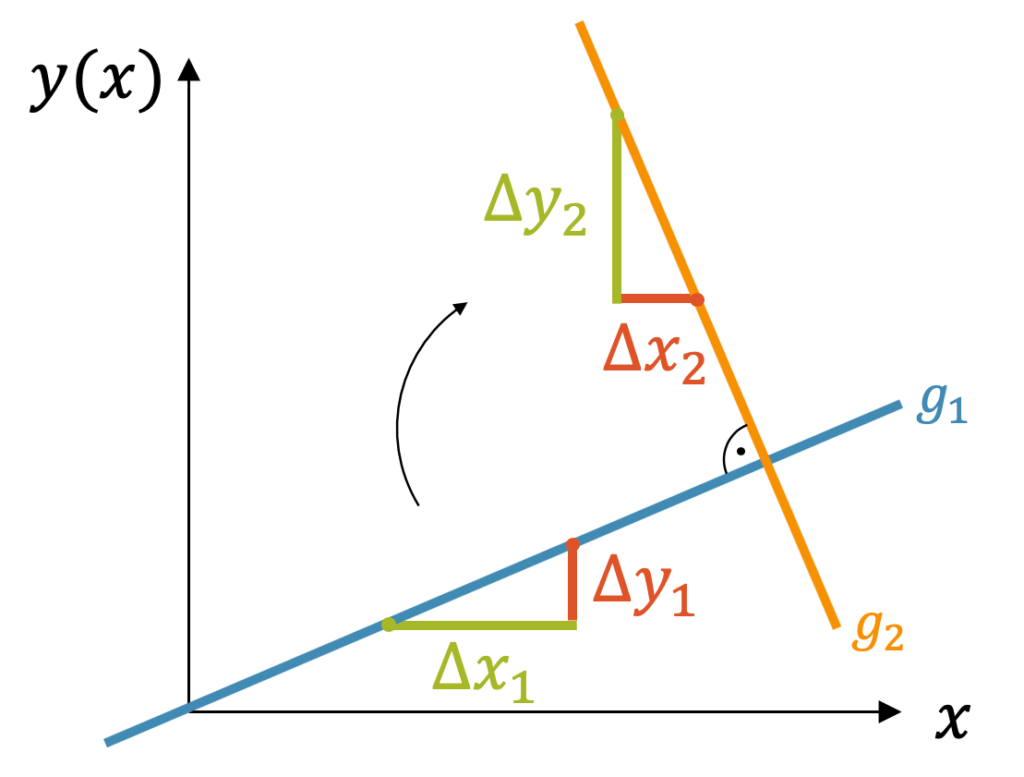
\[ \Delta x_1 \quad \rightarrow \quad \Delta y_2 \]
\[ \Delta y_1 \quad \rightarrow \quad -\Delta x_1 \]
Wenn wir das in der Gleichung der Steigung \(m_1\) einsetzen, erhalten wir:
\[ m_1 = \frac{\Delta y_1}{\Delta x_1} \quad \rightarrow \quad m_1 = \frac{-\Delta x_2}{\Delta y_2} = -\frac{1}{m_2} \]
Für die Steigungen \(m_1\) und \(m_2\) der beiden Geraden \(g_1\) und \(g_2\), die senkrecht aufeinander stehen, gilt:
\[ m_1 = -\frac{1}{m_2} \]
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.