Nullstellen
Unter Nullstellen verstehen wir die Schnittpunkte des Funktionsgraphen mit der \(x\)-Achse. Die \(x\)-Achse zeichnet sich dadurch aus, dass die \(y\)-Werte null sind, d.h. unsere Funktion kreuzt die \(x\)-Achse, wenn der Funktionswert null ist.
Wir erhalten die Nullstellen, indem wir die Funktionsgleichung auf null setzen.
Beachte, dass grundsätzlich mehr als eine Nullstelle möglich ist, d.h. der Funktionsgraph kann die x-Achse in mehreren Punkten schneiden. Im Gegensatz dazu gibt es vom Achsabschnitt immer nur einen Punkt, in welchem der Funktionsgraph die y-Achse schneidet.
Beispiel
Finde die Nullstelle der linearen Funktion \(f(x)=3x+6\).
Wir setzen die Funktionsgleichung auf null:
\[ 3x+6 \;\; \stackrel{!}{=} \;\; 0 \]
Wir lösen diese Gleichung nach \(x\) auf und subtrahieren als Erstes 6.
\[ 3x = -6 \]
Jetzt dividieren wir mit 3 und erhalten die Lösung für \(x\):
\[ \underline{x = -2} \]
Die Nullstelle liegt bei \(x=-2\), d.h. der Funktionsgraph schneidet die \(x\)-Achse an dieser Stelle.
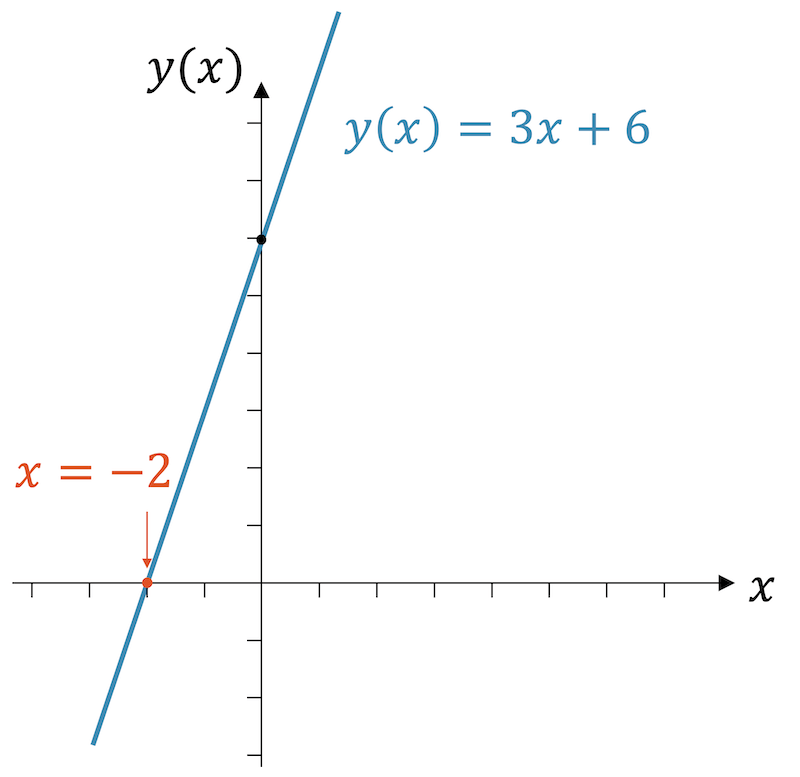
Beachte, dass es genau eine Lösung gibt, d.h. der Funktionsgraph schneidet die \(x\)-Achse nur an einem Ort. In anderen Fällen kann es mehr als eine Nullstelle geben. Gewisse Funktionen haben auch keine Nullstelle, weil der Funktionsverlauf die \(x\)-Achse gar nie schneidet.
Beispiel
Ermittle die Nullstellen der folgenden Funktion:
\[ f(x) = \frac{1}{5}x^3-\frac{8}{5}x^2+3x \]
Wir setzen die Funktionsgleichung gleich null und versuchen dann die linke Seite zu faktorisieren.
\[ \frac{1}{5}x^3-\frac{8}{5}x^2+3x = 0 \]
Als Erstes klammern wir \(\frac{1}{5}\) und \(x\) aus:
\[ \frac{1}{5} \cdot \Big( x^3- 8x^2 + 15x \Big) = 0 \]
\[ \frac{1}{5}x \cdot \Big( x^2- 8x + 15 \Big) = 0 \]
Den Klammerterm können wir mit dem Klammeransatz lösen:
\[ \frac{1}{5}x \cdot \Big( x-3 \Big) \cdot \Big(x-5 \Big) = 0 \]
Jetzt haben wir die linke Seite vollständig faktorisiert. Nun ist es sehr einfach zu ermitteln, für welche \(x\)-Werte die linke Seite null wird. Die linke Seite wird null, wenn nur einer der Faktoren null ist, d.h. für \(\underline{x=0}\), \(\underline{x=3}\) oder \(\underline{x=5}\). Die Funktion schneidet die \(x\)-Achse 3-mal und zwar genau an diesen Orten.
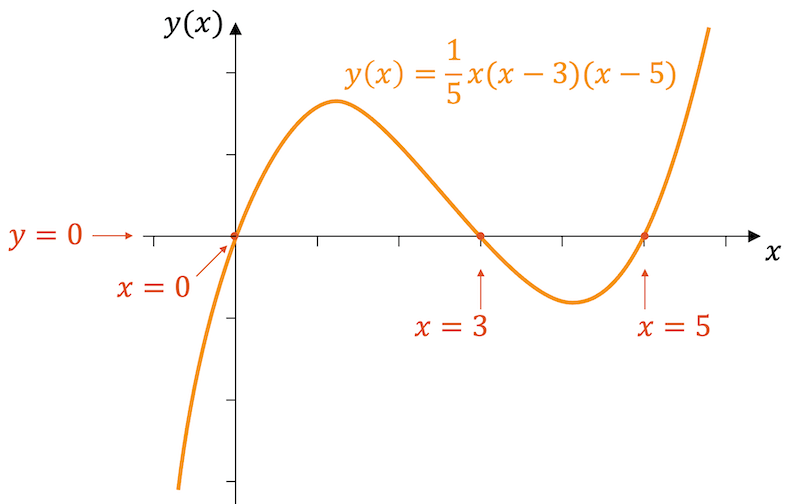
Für die Ermittlung der Nullstellen sollte der Ausdruck in der Funktionsgleichung faktorisiert werden, so dass die Teiler erkennbar werden. Das Gleichsetzen der Funktionsgleichung mit null kann dann sehr einfach gelöst werden: Die Gleichung ist null, wenn einer der Faktoren null ist.
Es gibt so viele Nullstellen wie es Teiler gibt, die null werden können.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.