Eine Funktion ist monoton steigend, wenn sie immer zunimmt oder mindestens gleich bleibt, aber nie abnimmt. Analog gilt eine Funktion als monoton fallend, wenn sie immer nur gleich bleibt oder abnimmt, aber nie zunimmt.
Unter streng monoton steigend oder fallend, verstehen wir immer steigend oder fallend und schliessen damit den Fall aus, in welchem die Funktion konstant bleibt.
Beispiel
Untersuche die folgenden Funktionsverläufe auf Monotonie.
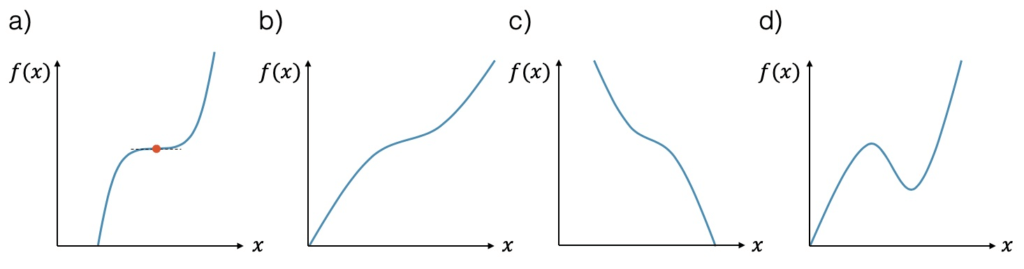
Für Kurvendiskussionen ist die Monotonie ein wichtiges Konzept. In der Abbildung sind verschiedene Verläufe dargestellt, die unterschiedliche Formen von Monotonie zeigen.
a) Die erste Grafik zeigt uns eine (von links nach rechts) steigende Kurve. Da die Funktionswerte (von links nach rechts) niemals abnehmen, sprechen wir hier von monoton steigend. Das Prädikat streng können wir hier nicht anwenden, da es einen sog. Terrassenpunkt gibt, einen Punkt mit Steigung null. Unmittelbar um diesen Punkt herum ist der Graph der Funktion horizontal und der Funktionswert nimmt nicht zu.
b) In der zweiten Grafik ist der Verlauf streng monoton steigend, denn die Steigung ist immer positiv und nie null.
c) Die dritte Grafik zeigt uns eine streng monoton fallende Kurve, denn auch hier ist die Steigung nie null.
d) Schliesslich haben wir in der vierten Grafik eine Funktion, die mal steigt und mal sinkt. Diese Funktion ist deshalb nicht monoton. Man könnte höchstens sagen, dass sie in gewissen Bereichen monoton oder sogar streng monoton verläuft.
Beispiel
Wie ist die Monotonie der folgenden Funktion \(f\) für \(\boldsymbol{D}=\mathbb{R}\) ?
\[ f(x)=-x^3 \]
Wir stellen eine kleine Wertetabelle auf:
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(f(x)\) | 8 | 1 | 0 | -1 | -8 |
Jetzt können wir den Verlauf skizzieren:
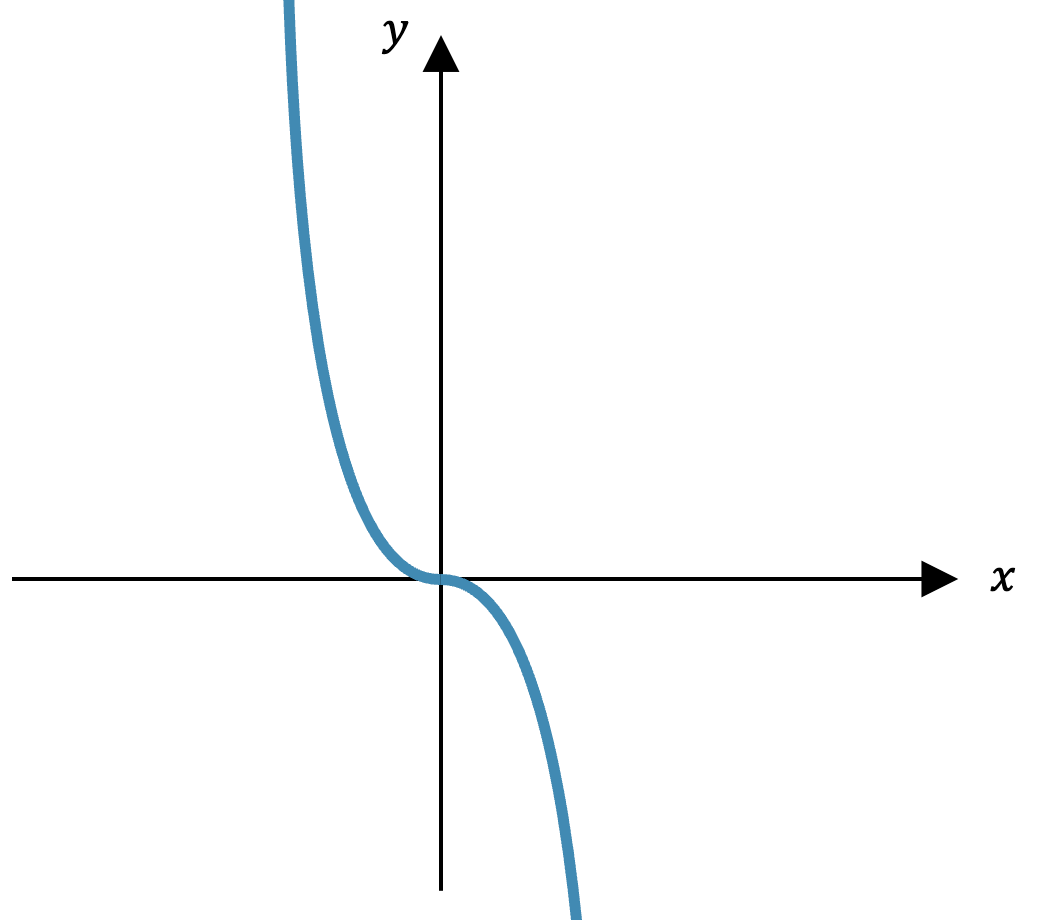
Was wir hier nicht erkennen können ist die Tatsache, dass im Ursprung (0,0) wir einen Terrassenpunkt haben, d.h. die Funktion ist monoton fallend.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.