Lineare Funktionen gehören zwar zu den einfacheren Funktionen. Sie sind aber vermutlich die meist verbreiteten Funktionen überhaupt. Wie der Name sagt, bilden lineare Funktionen Verläufe von geraden Linien. Alle anderen Funktionen werden einfach mit nicht linear bezeichnet, womit ein meist unbekannter, ”gekrümmter” Verlauf gemeint ist.
Lineare Grundfunktion
Das typische Merkmal der linearen Grundfunktion ist die Proportionalität. Klassisches Beispiel sind Menge und Preis: Wenn ich die doppelte Menge kaufen möchte, muss ich doppelt so viel bezahlen. Die 10-fache Menge kostet das 10-fache etc. Was sich nicht ändert ist der Preis für ein Stück.
Beachte: Sobald Mengenrabatte mit ins Spiel kommen, wird der Zusammenhang zwischen Menge und Preis nicht linear: Wenn ein Grosshändler für 1’000 Stück einen bestimmten Preis zahlt, so ist ein einzelnes Stück nicht zum Tausendstel des Preises zu bekommen!
Die lineare Grundfunktion hat folgende allgemeine Funktionsgleichung:
\[ f(x) = m \cdot x \]
Zwischen dem Argument \(x\) und dem Funktionswert \(y=f(x)\) besteht Proportionalität mit dem Proportionalitätsfaktor \(m\).
Der Achsabschnitt ist null.
Steigung
Lineare Funktionen bilden gerade Linien. Diese können gegenüber der \(x\)-Achse eine Steigung bzw. einen bestimmten Winkel einnehmen.
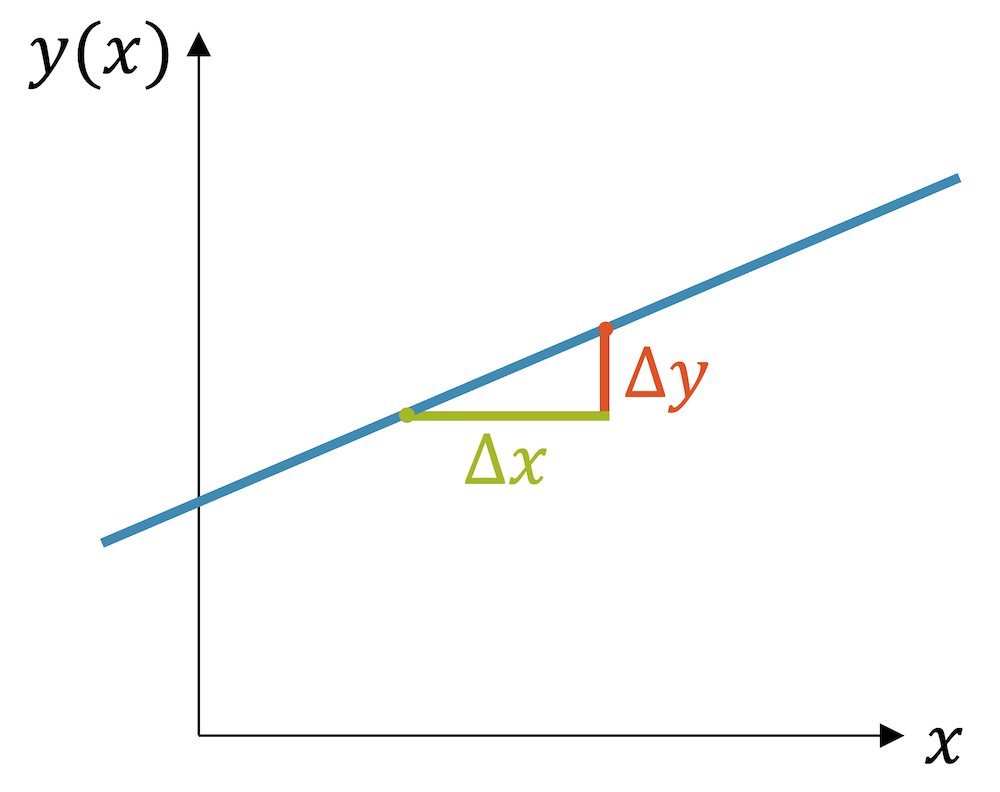
Die Steigung antwortet auf die Frage: Wie stark ändert sich der Funktionswert \(y\), wenn sich \(x\) verändert? Wir lassen also \(x\) um den Betrag \(\Delta x\) zunehmen, bewegen uns also leicht nach rechts. Die Funktion steigt dabei um \(\Delta y\).
Bei gleichem \(\Delta x\) nimmt \(y\) bei einer steilen Geraden sehr stark zu, bei einer relativ flachen Geraden wenig, bei einer fallenden Geraden nimmt \(y\) sogar ab.
Die Steigung \(m\) einer linearen Funktion ist definiert als:
\[ m=\frac{\Delta y}{\Delta x} \]
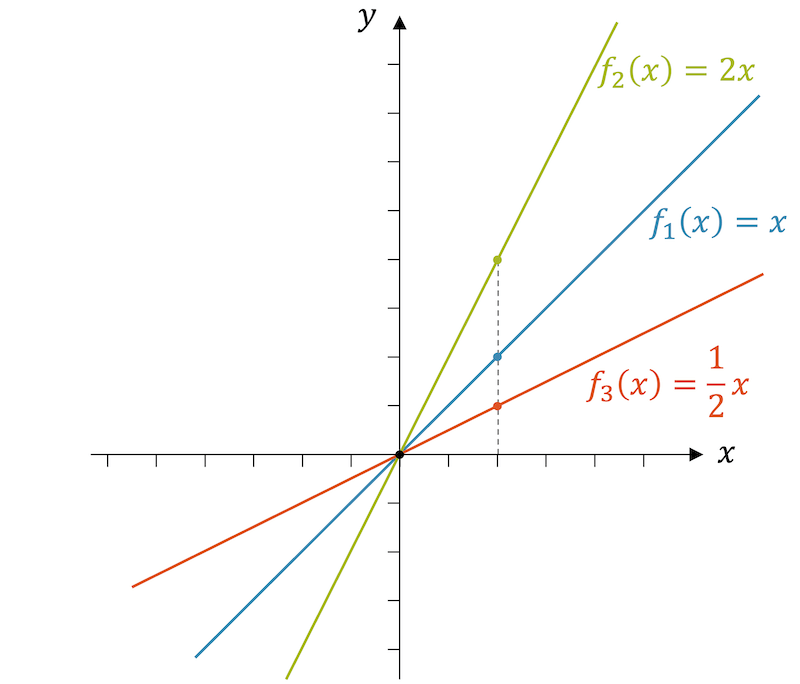
In der obigen Abbildung sind drei lineare Funktionen mit verschiedenen Steigungen eingezeichnet.
\[ f_1(x) = x, \quad \quad f_2(x) = 2x, \quad \quad f_3(x) = \frac{1}{2}x \]
Wir starten mit der blauen Grundgleichung für lineare Funktionen:
\[ f_1(x)=x \]
Um die Steigung \(m\) zu bestimmen, benötigen wir \(\Delta y\) und \(\Delta x\). Ausgehend vom Ursprung zu den eingezeichneten Punkten gilt \(\Delta x = 2\). Für die blaue Funktion \(f_1(x)\) gilt \(\Delta y = 2\) und somit:
\[ m_1 = \frac{\Delta y}{\Delta x} = \frac{2}{2} = 1 \]
Analog erhalten wir für die grüne Funktion \(m_2=2\) und für die rote Funktion die Steigung \(m_3=\frac{1}{2}\). Wir erkennen, dass die Steigung dem Proportionalitätsfaktor \(m\) vor dem \(x\) in der Funktionsgleichung entspricht.
Interpretation der Steigung \(m\) (Betrachtung von links nach rechts):
- \(m>0\): Steigende lineare Funktion, je grösser \(m\), desto steiler nach oben
- \(m=0\): Horizontale lineare Funktion
- \(m<0\): Abfallende lineare Funktion, je negativer \(m\), desto steiler nach unten
Funktionsgleichung
Die drei linearen Funktionen, die wir angeschaut haben, gingen alle durch den Nullpunkt. Im allgemeinen muss das aber nicht so sein. Die lineare Funktion kann die \(y\)-Achse an einem beliebigen Punkt schneiden. Starten wir wieder mit der Grundfunktion der linearen Funktionen: \(y(x)=x\). Wir verlangen jetzt aber, dass sie auf der Höhe \(q\) die \(y\)-Achse schneidet, d.h. sie muss um den Betrag \(q\) angehoben werden.
Wir wissen, wie ein Funktionsgraph um \(q\) nach oben verschoben werden muss: Wir addieren einfach den Betrag \(q\) zur Grundfunktion und erhalten die allgemeinste Gleichung für lineare Funktionen:
Lineare Funktionen haben die folgende allgemeine Funktionsgleichung:
\[ f(x) = m \cdot x + q \]
Dabei ist \(m\) die Steigung der linearen Funktion und \(q\) ist der Achsabschnitt.
Beispiel
Eine lineare Funktion hat folgende Wertetabelle. finde die Steigung \(m\) und den Achsabschnitt \(q\).
| \(x\) | -20 | -8 | -4 | 4 | 12 |
| \(f(x)\) | 3 | 0 | -1 | -3 | -5 |
Wir nehmen z.B. die letzten beiden Spalten und bilden eine Differenz der \(x\)-Werte:
\[ \Delta x = 12 – 4 = 8 \]
Dann bilden wir in gleicher Weise die Differenz der beiden zugehörigen Funktionswerte \(y=f(x)\):
\[ \Delta y = -5 – (-3) = -2 \]
Jetzt können wir die Steigung \(m\) berechnen:
\[ m = \frac{\Delta y}{\Delta x} = \frac{-2}{8} = \underline{-\frac{1}{4}} \]
Für den Achsabschnitt der Funktion brauchen wir den Funktionswert für \(x=0\), denn dort ist die \(y\)-Achse. Leider kommt der Wert \(x=0\) in der Tabelle nicht vor. Wir stellen deshalb die Funktionsgleichung auf und setzen ein beliebiges Wertepaar ein. Wir wählen das Wertepaar \(x=4\) und \(y=-3\).
\[ f(x) = m \cdot x + q = -\frac{1}{4}x + q \]
\[ f(4) = -\frac{1}{4} \cdot 4 + q = -3 \]
Wir erhalten eine Gleichung mit der Unbekannten \(q\), die wir bestimmen möchten:
\[ -1 + q = -3 \]
\[ \underline{q = -2} \]
Damit haben wir den Achsabschnitt der Funktion gefunden, d.h. \(f(0)=-2\).
Parallele Geraden haben die gleiche Steigung:
\[ m_1 = m_2 \qquad \Leftrightarrow \qquad f_1\;\parallel\;f_2 \]
Spezielle lineare Funktionen
Beispiel
Bestimme die Funktionsgleichung, sowie die Definitions- und Wertebereiche der folgenden Funktionen \(f_1\) und \(f_2\):
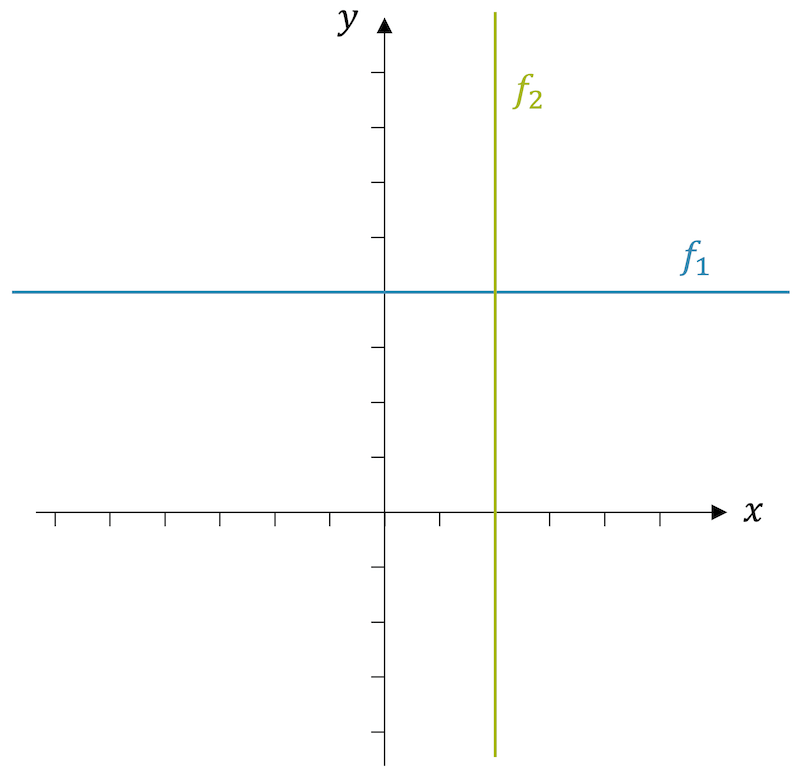
Die erste Funktion \(f_1\) hat immer den gleichen Funktionswert, nämlich 4, unabhängig vom Wert von \(x\). Deshalb schreiben wir “gleich vier für alle Werte von \(x\)”:
\[ f_1(x)=4 \quad \forall x \in \mathbb{R} \]
Die Definitionsmenge \(\mathds{D_1}\) ist \(\mathbb{R}\), weil alle Werte von \(x\) erlaubt sind:
\[ \underline{\mathds{D_1} = \mathbb{R}} \]
Die Wertemenge \(\mathds{W_1}\) enthält nur gerade ein Element:
\[ \underline{\mathds{W_1} = \big\{ 4 \big\}} \]
Bei der zweiten Funktion ist nur ein \(x\)-Wert erlaubt, nämlich \(x=2\). Für alle anderen \(x\)-Werte ist die Funktion nicht definiert. Wir schreiben deshalb:
\[ \underline{\mathds{D_2} = \big\{ 2 \big\}} \]
Für \(x=2\) nimmt die Funktion alle \(y\)-Werte an. Deshalb gilt:
\[ \underline{\mathds{W_2} = \mathbb{R}} \]
Beachte, dass \(f_2\) keine korrekte Funktion ist, denn sie ordnet nicht einem \(x\)-Wert auf eindeutige Weise einen Funktionswert zu. Als Gleichung können wir aber schreiben:
\[ \underline{x=2} \]
Für zwei aufeinander senkrecht stehende Geraden ist die eine Steigung gleich dem negativen Kehrwert der anderen Steigung:
\[ m_1 = -\frac{1}{m_2} \qquad \Leftrightarrow \qquad f_1\;\perp\;f_2 \]
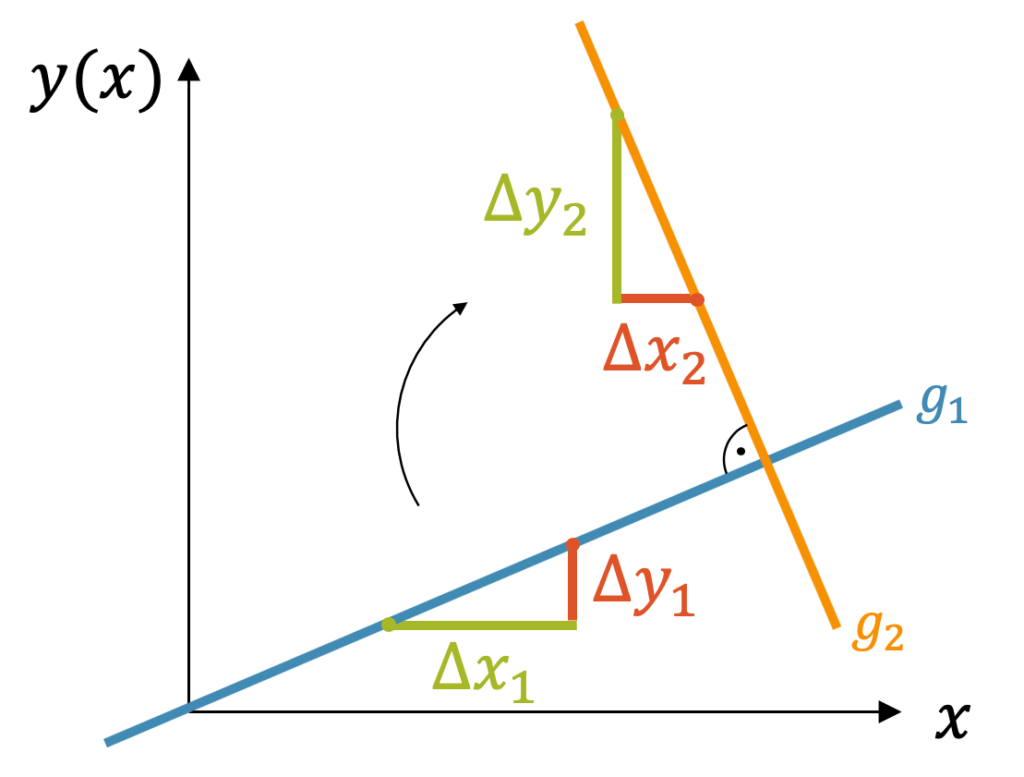
In der obigen Grafik sind zwei senkrecht aufeinander stehende lineare Funktionen \(g_1\) und \(g_2\) gezeichnet. Für die Funktion \(g_1\) gilt:
\[ m_1 = \frac{\Delta y_1}{\Delta x_1} \]
Wenn wir das Steigungsdreieck um 90° im Uhrzeigersinn drehen, gilt:
\[ \Delta x_2 = \Delta y_1 \quad \quad \quad -\Delta y_2 = \Delta x_1 \]
Beim \(\Delta y_2\) mussten wir ein negatives Zeichen setzen, denn die Funktion fällt von links nach rechts ab, d.h. \(\Delta y_2\) ist negativ. \(\Delta x_1\) ist positiv und hat den gleichen Betrag wie \(\Delta y_2\), aber eben ein umgekehrtes Vorzeichen.
Für \(m_2\) gilt ja grundsätzlich:
\[ m_2 = \frac{\Delta y_2}{\Delta x_2} \]
Sobald wir jetzt aber die Gleichungen von oben einsetzen, erhalten wir:
\[ m_2 = \frac{-\Delta x_1}{\Delta y_1} = – \frac{\Delta x_1}{\Delta y_1} \]
Der Bruch ist genau der Kehrbruch von \(m_1\). Somit haben wir tatsächlich: \(m_2 = – \frac{1}{m_1}\)
Lineare Funktion aus zwei Punkten
Aus der Geometrie wissen wir, dass eine Gerade durch zwei Punkte eindeutig bestimmt ist. Mit einem Punkt wäre die Gerade in diesem Punkt fixiert, die Steigung könnte aber beliebig verändert werden oder andersrum: Wir könnten die Gerade beliebig drehen und sie würde weiterhin durch diesen Punkt gehen. Bei zwei Punkten ist die Sache anders: Die Gerade ist eindeutig bestimmt.
Die Frage, der wir uns jetzt stellen ist, wie bestimmen wir die lineare Funktion, wenn wir zwei beliebige Punkte als Information haben. Wir erinnern uns: Um die Funktionsgleichung aufstellen zu können, brauchen wir nur zwei Dinge zu ermitteln:
- Was ist die Steigung \(m\)?
- Was ist der Achsabschnitt \(q\), d.h. auf welcher Höhe schneidet die Gerade die \(y\)-Achse?
Beispiel
Wie ist die Funktionsgleichung der Geraden, die durch die Punkte A(3,2) und B(2,-2) geht?
Als Erstes bestimmen wir die Steigung \(m\): Wir brauchen ein \(\Delta x\) und ein \(\Delta y\). Wir müssen nur vom einen zum anderen Punkt gehen und schauen, um wie viel \(x\) und \(y\) sich verändert haben.
\[ \Delta x = 2-3 = -1 \]
\[ \Delta y = -2-2 = -4 \]
Damit berechnen wir die Steigung:
\[ m=\frac{\Delta y}{\Delta x}=\frac{-4}{-1}=4 \]
Wir haben schon die Hälfte der Funktionsgleichung herausgefunden! Wir schreiben sie auf und setzen einfach \(q\) ein, weil wir es noch nicht kennen.
\[ f(x)=4x+q \]
Wir nehmen irgendein ein Wertepaar \((x,y)\), das zur Funktion gehört, z.B. den Punkt A(3,2) und setzen sie in die Funktionsgleichung ein:
\[ f(3) = 4 \cdot 3 + q = 2 \]
Somit haben wir eine Gleichung mit einer Unbekannten \(q\):
\[ 12 + q = 2 \]
\[ q = -10 \]
Der Punkt B(2,-2) hätte uns das gleiche Resultat geliefert. Nur für diejenigen, die mir das nicht glauben:
\[ f(2) = 4 \cdot 2 + q = -2 \]
\[ 8 + q = -2 \]
Die Funktionsgeichung der Geraden lautet somit:
\[ \underline{f(x)=4x-10} \]
Um die Funktionsgleichung einer linearen Funktion \(f(x)=m \cdot x + q\) zu bestimmen, braucht es zwei Punkte mit ihren Koordinaten \((x_1,y_1)\) und \((x_2,y_2)\).
Die Steigung \(m\) wird bestimmt, indem die Differenz der \(x\)- und \(y\)-Koordinaten der gegebenen Punkte berechnet wird:
\[ m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1} \]
Der Achsabschnitt wird aus einem der beiden Punkte berechnet:
\[ q=f(x)-m \cdot x = y_1-m \cdot x_1 = y_2-m \cdot x_2 \]
Beispiel
Wie lautet die Funktionsgleichung der Geraden, die die x-Achse in \((3,0)\) und die y-Achse in \((0,-2)\) schneidet?
Als Erstes nehmen wir uns den Achsabschnitt vor. Wir wissen, wo die Gerade die \(y\)-Achse schneidet, auf der Höhe -2, d.h. \(q=-2\).
Jetzt bestimmen wir die Steigung. Wir brauchen ein \(\Delta x\) und das dazugehörige \(\Delta y\). Die Aufgabenstellung gibt uns ja zwei Punkte, die auf der Geraden liegen. Wir können einfach diese beiden Punkte nehmen und die \(\Delta x\) und \(\Delta y\) zwischen ihnen bestimmen.
Der \(x\)-Unterschied zwischen den beiden Punkten beträgt: \(\Delta x = 3-0 = 3\). Der \(y\)-Unterschied ist \(\Delta y = 0 – (-2) = 2\). Die Gerade steigt somit um \(\Delta y = 2\), bei \(\Delta x = 3\) und die Steigung beträgt
\[ m=\frac{\Delta y}{\Delta x}=\frac{2}{3} \]
Die Funktionsgleichung der Geraden ist deshalb:
\[ \underline{f(x)=\frac{2}{3} \cdot x – 2} \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.