Die Eigenschaft gerade oder ungerade zu sein, ist nur für wenige Funktionen anwendbar. Die meisten Funktionen sind weder noch. Es ist aber eine wichtige und nützliche Eigenschaft, die wir immer wieder verwenden werden. Deshalb ist es wichtig, diese Eigenschaft zu kennen.
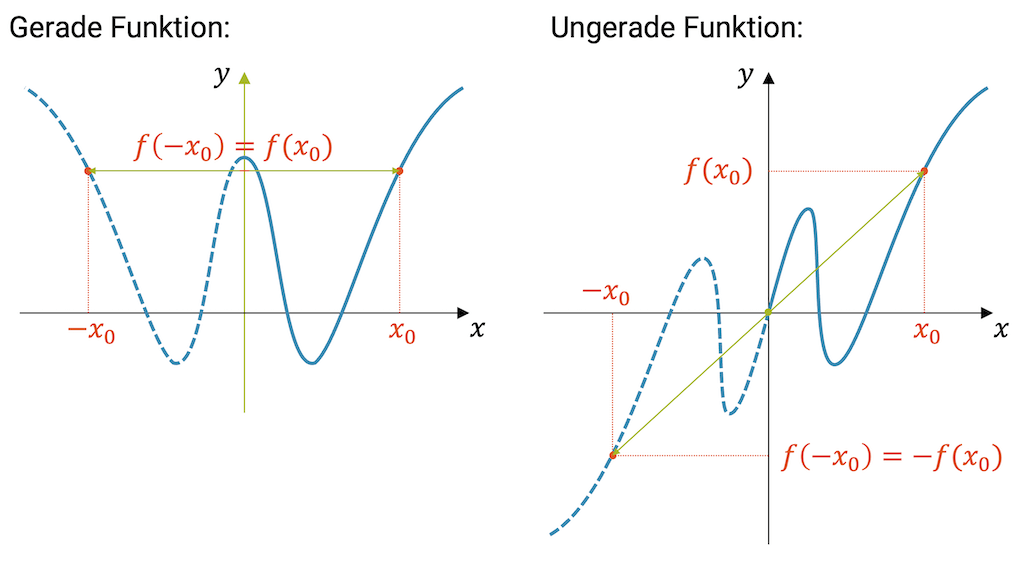
Gerade Funktionen sind spiegelsymmetrisch bezüglich der \(y\)-Achse:
\[ f(x) = f(-x) \]
Ungerade Funktionen sind punktsymmetrisch bezüglich dem Ursprung:
\[ f(x) = -f(-x) \]
Wenn wir das Vorzeichen des Arguments umkehren, dann ändert das nichts am Funktionswert der geraden Funktion. Denn die gerade Funktion liefert für \(x\) und für \((-x)\) den gleichen Funktionswert. Der Funktionsverlauf ist spiegelsymmetrisch zur \(y\)-Achse.
Bei der ungeraden Funktion haben wir eine Punktsymmetrie bezüglich dem Ursprung. Das Umkehren des Vorzeichens des Arguments führt zu einem umgekehrten Vorzeichen beim Funktionswert.
Beispiel
Untersuche die Quadratfunktion \(f(x)=x^2\) darauf, ob sie die Eigenschaft gerade oder ungerade oder keine von beiden hat.
Der Funktionsgraph der Quadratfunktion ist eine Parabel und sie ist um die y-Achse spiegelsymmetrisch. Wir nehmen irgendeinen \(x\)-Wert, z.B. \(x=3\) und schauen, ob die Funktion für den ‘’Spiegelpunkt’’ \(x=-3\) den gleichen Wert ergibt:
\[ f(3)=3^2=9 \]
\[ f(-3)=(-3)^2=9 \]
Das könnte aber auch ein Glückstreffer sein! Deshalb untersuchen wir diese Eigenschaft für einen beliebiges Argument \(x\):
\[ f(x) = x^2 \quad , \quad f(-x) = (-x)^2 = x^2 \quad \Rightarrow \quad \underline{f(x) = f(-x)} \]
Die Funktion \(f(x)=x^2\) erfüllt die Eigenschaft einer geraden Funktion für alle \(x\).
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.