Das Wichtigste in Kürze
Streckung des Funktionsverlaufs in vertikaler Richtung:
Die Original-Funktion sei \(f(x)\). Wir können einen neuen Funktionsgraphen \(g(x)\) erhalten, der um den Faktor \(\boldsymbol{k}\), von der \(x\)-Achse aus, in vertikaler Richtung gestreckt ist, mit:
\[ g(x)=\boldsymbol{k} \cdot f(x) \]
Wenn \(\boldsymbol{k}<1\) ist, wird die Funktion entsprechend gestaucht. Der Faktor der Stauchung entspricht dem Kehrwert \(\frac{1}{k}\).
Stauchung des Funktionsverlaufs in horizontaler Richtung:
Aus der Funktion \(f(x)\) erhalten wir die neue Funktion \(g(x)\), die um \(\boldsymbol{k}>1\) in der Horizontalen gestaucht ist, mit:
\[ g(x)=f(\boldsymbol{k} \cdot x) \]
Wenn der Graph um den Faktor \(\boldsymbol{k}>1\) in der Horizontalen gestreckt werden soll, multiplizieren wir das Argument mit dem Kehrwert \(\frac{1}{k}\)
\[ g(x)=f(\frac{1}{\boldsymbol{k}} \cdot x) \]
Häufigste Fragen
Funktionen vertikal strecken und stauchen
Wenn wir jeden Funktionswert mit einem Faktor \(k\) multiplizieren, dann wird der Verlauf der Funktion von der \(x\)-Achse her nach oben gestreckt.
Sie wird aber auch unterhalb der \(x\)-Achse nach unten gestreckt, denn die negativen Funktionswerte werden mit den Streckfaktor multipliziert und sind dann noch negativer.
Streckung des Funktionsverlaufs in vertikaler Richtung:
Die Funktionswerte der Original-Funktion \(f(x)\) werden mit dem Faktor \(k\) multipliziert. Wir erhalten so einen neuen Funktionsgraphen \(g(x)\), der um den Faktor \(\boldsymbol{k}\) in vertikaler Richtung gestreckt ist:
\[ g(x)=\boldsymbol{k} \cdot f(x) \]
Wenn \(\boldsymbol{k}<1\) ist, wird die Funktion entsprechend gestaucht. Der Faktor der Stauchung entspricht dem Kehrwert \(\frac{1}{k}\).
Stauchung des Funktionsverlaufs in vertikaler Richtung mit Faktor \(k\) (Streckung mit Faktor \(\frac{1}{k}\)):
\[ g(x)=\frac{1}{\boldsymbol{k}} \cdot f(x) \]
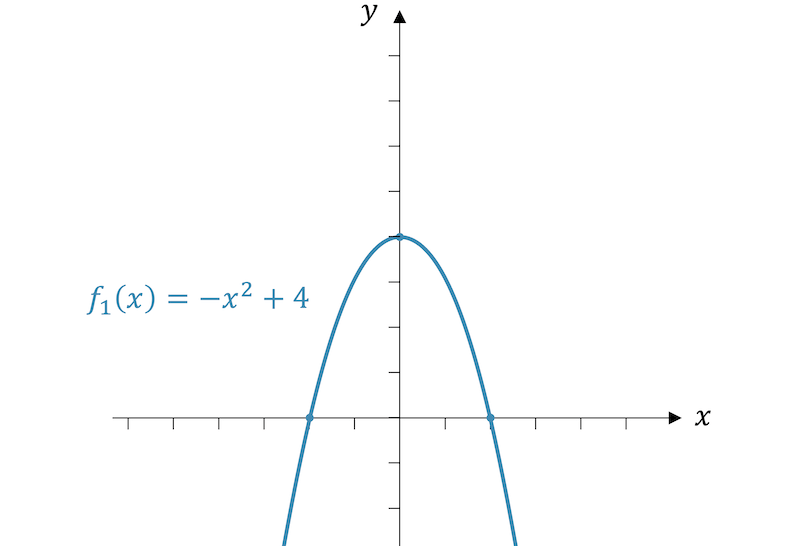
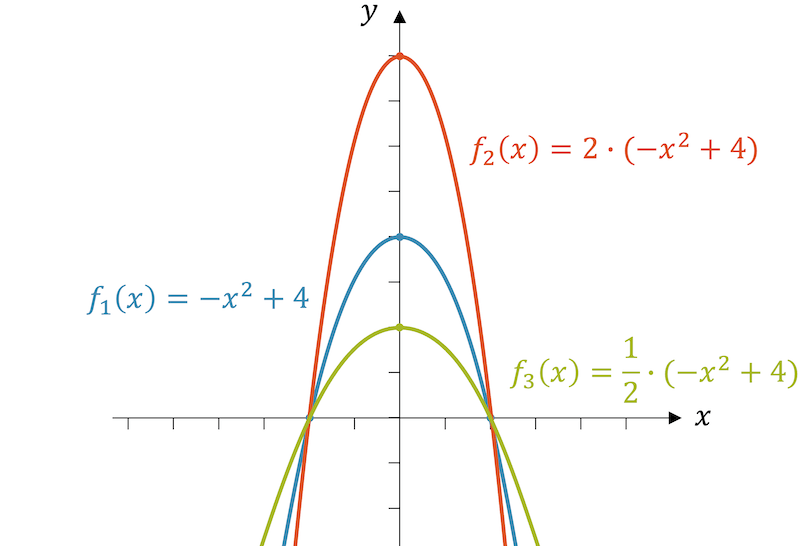
Beispiel: Vertikale Streckung / Stauchung
Strecke und stauche die Funktion \(f_1(x)\) vertikal mit dem Faktor 2 und zeige, dass der Achsabschnitt wie erwartet auf der \(y\)-Achse höher bzw. tiefer zu liegen kommt.
Mit dem Faktor 2 gestreckt, sollte der Achsabschnitt von (+4) auf (+8) gehen. Wir multiplizieren die Funktionsgleichung mit dem Faktor 2 und erhalten:
\[ f_2(x) = 2 \cdot \big(-x^2+4\big) \]
Wir multiplizieren aus und erhalten:
\[ f_2(x) = -2x^2 + 8 \]
Tatsächlich haben wir jetzt einen Achsabschnitt von (+8). Analog geht es mit einer Stauchung mit Faktor 2, was einer Streckung mit dem Kehrwert \(\frac{1}{2}\) entspricht.
\[ f_3(x) = \frac{1}{2} \cdot \big(-x^2+4\big) \]
\[ f_3(x) = -\frac{1}{2}x^2 + 2 \]
Der Achsabschnitt rutscht auf (+2) herunter.
Beachte, dass die Nullstellen sich durch das Strecken oder Stauchen nicht verändert haben. Das hat damit zu tun, dass das Strecken und Stauchen von der \(x\)-Achse aus geht, d.h. die \(x\)-Achse selber bleibt unverändert.
“Strecken und stauchen in der Horizontalen: Einfach die Änderung an der Funktionsvariablen (Argument) vornehmen und daran denken: Ist immer umgekehrt!”
Funktionen horizontal strecken und stauchen
Wie schon beim Verschieben von Funktionen, müssen wir jetzt die Funktionsvariable \(x\) verändern, statt den Funktionswert \(y=f(x)\) und wir müssen umdenken, weil es immer etwas umgekehrt ist.
Eine Multiplikation der Funktionsvariablen \(x\) mit dem Streckfaktor \(k\) für jetzt zu einer horizontalen Stauchung:
\[ g(x)=f(\boldsymbol{k} \cdot x) \]
Wenn es uns aber um eine horizontale Streckung mit dem Faktor \(k\) geht, stauchen wir mit dem Kehrwert \(\frac{1}{k}\):
\[ g(x)=f(\frac{1}{\boldsymbol{k}} \cdot x) \]
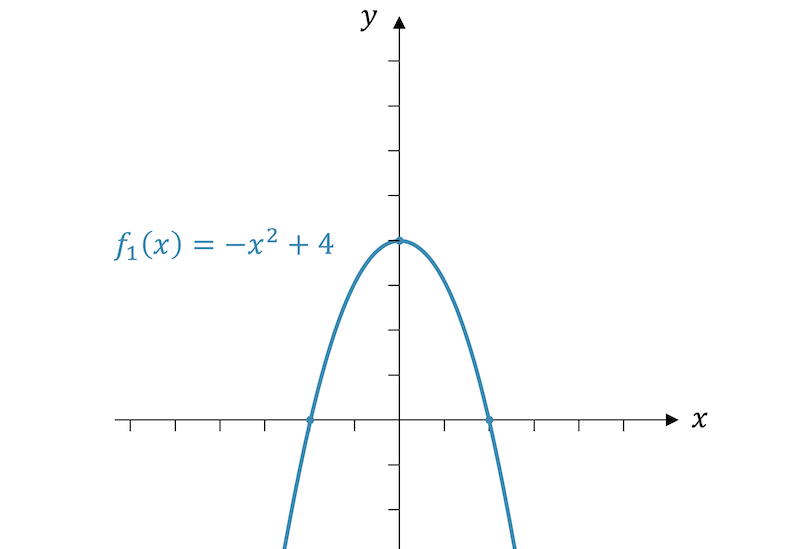
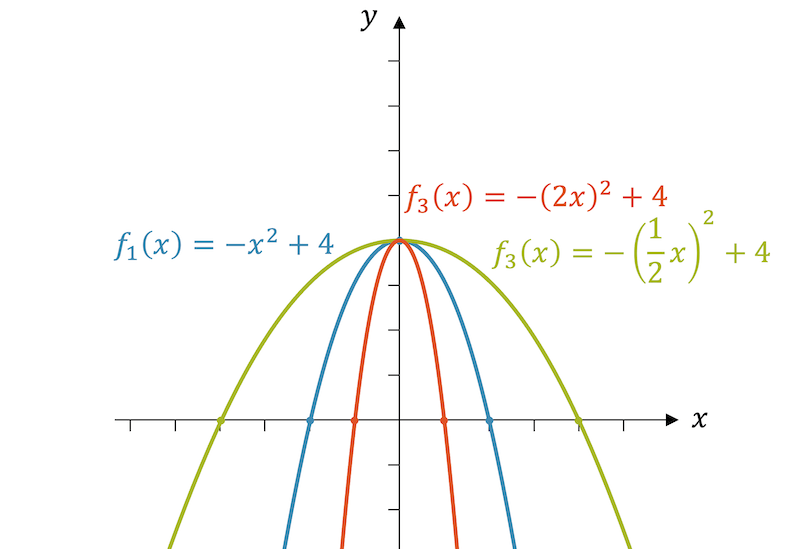
Beispiel: Horizontale Streckung / Stauchung
Strecke und stauche die Funktion \(f_1(x)=-x^2+4\) dieses Mal horizontal mit dem Faktor 2 und zeige, dass der Achsabschnitt gleich bleibt. Zeige auch, dass der Abstand zwischen den Nullstellen sich verdoppelt bzw. halbiert.
Hier sind die Verläufe der gestreckten und gestauchten Funktion. Beachte, dass der Abstand der beiden Nullstellen der ursprünglichen Funktion \(f_1(x)\) genau 4 beträgt.
Wenn wir das Argument in der Funktion mit dem Faktor 2 multiplizieren, so wird der Funktionsverlauf um den Faktor 2 gestaucht.
\[ f_2(x) = f_1(2x) = -(2x)^2 + 4 \]
\[ f_2(x) = -4x^2 + 4 \]
Wenn wir die Funktion horizontal strecken möchten, dann müssen wir das Argument in der Funktion mit dem Kehrwert von 2 multiplizieren, d.h. durch 2 dividieren:
\[ f_3(x) = f_1\Big(\frac{1}{2}x\Big) = -\Big(\frac{1}{2}x\Big)^2 + 4 \]
\[ f_3(x) = -\frac{1}{4}x^2 + 4 \]
Wir sehen, dass in beiden Fällen der Achsabschnitt nicht verändert wurde: Er beträgt immer noch (+4).
Schauen wir uns jetzt die Nullstellen an. Wir setzen die gestauchte Funktion \(f_2(x)\) zu null und lösen nach \(x\) auf:
\[ f_2(x) = -4x^2 + 4 \;\; \stackrel{!}{=} \;\; 0 \]
\[ -4x^2 = -4 \]
\[ x^2 = 1 \]
Diese Gleichung wird für zwei \(x\)-Werte erfüllt. Sicher für \(x=1\), aber auch für \(x=-1\). Das sind unsere beiden Nullstellen, die einen Abstand von 2 zueinander haben. Er ist tatsächlich zweimal kleiner als bei der ursprünglichen Funktion.
Für die gestreckte Funktion \(f_3(x)\) gehen wir analog vor:
\[ f_3(x) = -\frac{1}{4}x^2 + 4 \;\; \stackrel{!}{=} \;\; 0 \]
\[ -\frac{1}{4}x^2 = -4 \]
\[ -x^2 = -16 \]
\[ x^2 = 16 \]
Diese Gleichung hat auch wieder zwei Lösungen, nämlich \(x=4\) und \(x=-4\). Der Abstand zwischen den beiden Nullstellen beträgt also 8, doppelt so viel wie bei der ursprünglichen Funktion.
Aufgabensammlung
Lernziele
- Du kannst gegebene Funktionen vertikal und horizontal strecken bzw. stauchen und die neuen Funktionsgleichungen hinschreiben
- Du kannst (in einfachen Fällen) den Vorgang des Streckens und Stauchens rückgängig machen und so eine Funktion als Streckung bzw. Stauchung einer anderen Funktion deuten.
Weitere Links
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Kommentar oder Frage schreiben
Du musst angemeldet sein, um einen Kommentar abzugeben.