Das Wichtigste in Kürze
Der Achsabschnitt \((0,y_0)\) ist der Schnittpunkt des Funktionsverlaufs mit der \(y\)-Achse. Der Achsabschnitt ist ein einfacher und schnell zu ermittelnder Punkt und es lohnt sich deshalb, diesen gleich als Erstes zu ermitteln:
\[ f(0) = y_0 \]
Nullstellen und Achsabschnitt sind die Schnittpunkte des Funktionsgraphen mit der x-Achse (Nullstellen) und mit der y-Achse (Achsabschnitt).
Wir schauen uns zuerst den Achsabschnitt an. Er ist der Schnittpunkt des Funktionsgraphen mit der \(y\)-Achse. Die \(y\)-Achse zeichnet sich dadurch aus, dass die \(x\)-Werte null sind.
Wir erhalten deshalb den Achsabschnitt indem wir für \(x=0\) einsetzen.
Der Achsabschnitt \((0,y_0)\) ist der Schnittpunkt des Funktionsverlaufs mit der \(y\)-Achse. Der Achsabschnitt ist ein einfacher und schnell zu ermittelnder Punkt und es lohnt sich deshalb, diesen gleich als Erstes zu ermitteln:
\[ f(0) = y_0 \]
Beachte, dass es immer nur genau einen Achsabschnitt gibt, d.h. die \(y\)-Achse wird nur in einem Punkt geschnitten. Wenn der \(x=0\)-Wert nicht in der Definitionsmenge der Funktion ist, d.h. wenn die Funktion für \(x=0\) nicht definiert ist, gibt es auch keinen Achsabschnitt. Im Gegensatz dazu gibt es bei den Nullstellen durchaus auch mehr als eine Nullstelle.
Beispiel: Achsabschnitt einer linearen Funktion
Finde den Achsabschnitt der linearen Funktion \(f(x)=3x+6\) auf der \(y\)-Achse.
Beispiel: Achsabschnitt bestimmen
Bestimme den Achsabschnitt der folgenden Funktion:
\[ f(x) = x^5 -4x^4 + (x-2)^3 +x^2 -7x + 2 \]
Beispiel: Achsabschnitt ermitteln
Ermittle den Achsabschnitt der folgenden Funktion:
\[ f(x) = \frac{1}{5}x^3-\frac{8}{5}x^2+3x \]
y-Achsenabschnitt (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.

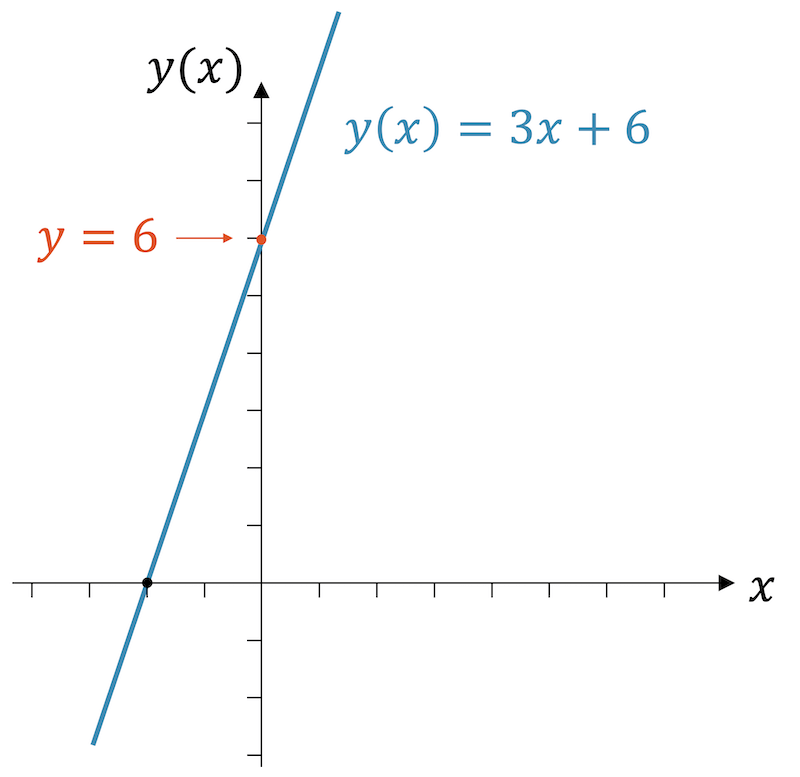


Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.