Du kennst vielleicht die unbestimmten Integrale. Wenn wir sie lösen, erhalten wir die Stammfunktion plus eine Konstante. Im Gegensatz zu den bestimmten Integralen haben unbestimmte Integrale keine Grenzen angegeben.
Uneigentliche Integrale haben zwar Grenzen, jedoch ist mindestens eine davon \(\infty\) oder \(-\infty\). Integrale können beide Grenzen uneigentlich sein und dabei von \(-\infty\) bis \(\infty\) laufen. Folgende Integrale sind uneigentliche Integrale:
\[ \int_a^{\infty} f(x) \; dx \]
\[ \int_{-\infty}^b g(x) \; dx \]
\[ \int_{-\infty}^{\infty} h(t) \; dt \]
Da \(\pm \infty\) keine Zahlen sind, müssen wir uns mit Grenzwerten behelfen:
Beispiel
Wie gross ist die Fläche \(A_2\)?
\[ A_2 = \int_1^{\infty} \frac{1}{x^2} \; dx \]
Die Funktion \(\frac{1}{x^2}\) ist eine Hyperbel. Es ist eine fallende Kurve. Ab \(x=1\) ist sie kleiner als \(1\) und nähert sich immer mehr der \(x\)-Achse.
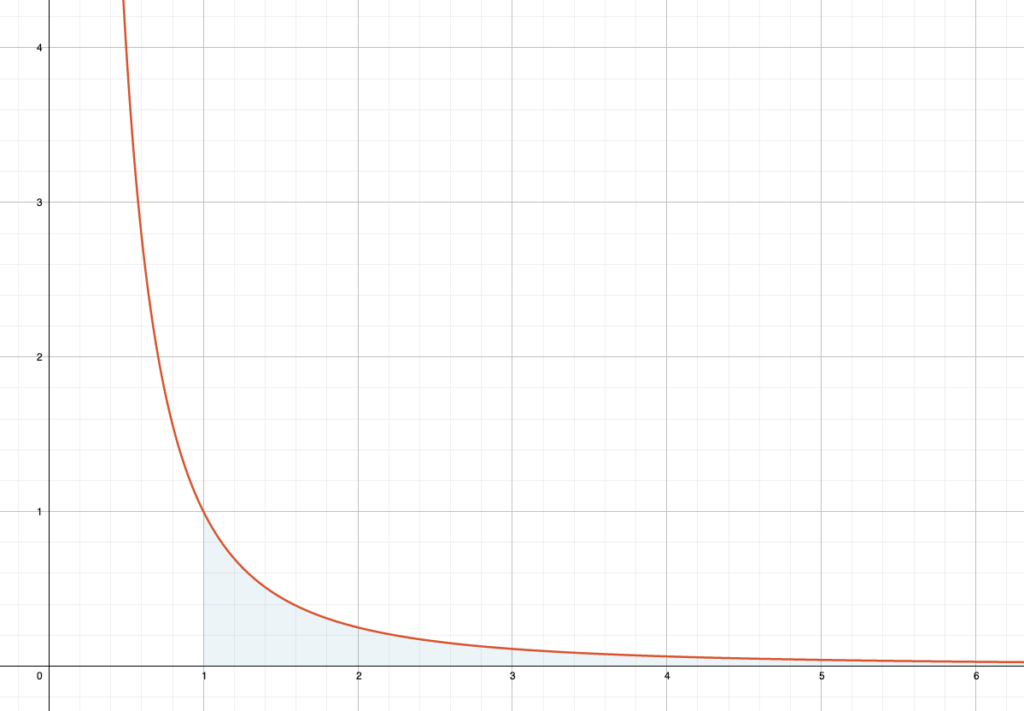
Das Integral stellt die Fläche dar, die nach rechts unendlich fortgesetzt wird. Allerdings wird die Fläche nach rechts immer dünner.
Wir ersetzen die obere Grenze (\(\infty\)) mit einer Variablen, z.B. \(b\) und lassen diese Variable in einem Grenzwert ins Unendliche laufen: \(b \rightarrow \infty\)
\[ A_2 = \lim_{b \rightarrow \infty} \Big( \int_1^b \frac{1}{x^2} \; dx \Big) \]
Nun ist das Integral kein uneigentliches Integral mehr, denn die Grenze heisst \(b\) und ist eine Zahl, auch wenn diese variabel ist. Der Grenzwert hat uns die Sache mit der unendlichen Integrationsgrenze “entschärft” und wir können es jetzt ausrechnen und danach den Grenzwert bilden.
\[ A_2 = \lim_{b \rightarrow \infty} \Big(\big [ -\frac{1}{x} \big ]_1^b \Big) \]
\[ = \lim_{b \rightarrow \infty} \Big(-\frac{1}{b} – \big( -\frac{1}{1} \big) \Big) \]
\[ = \lim_{b \rightarrow \infty} \Big( 1 – \frac{1}{b} \Big) \]
\[ = \lim_{b \rightarrow \infty} \Big( 1 \Big) – \lim_{b \rightarrow \infty} \Big( \frac{1}{b} \Big) \]
Die eins können wir aus dem Grenzwert herausnehmen, denn sie verändert sich nicht, wenn \(b\) gegen Unendlich läuft. Der zweite Grenzwert lässt sich auch angeben. Wenn \(b\) unendlich gross wird, geht der Kehrwert gegen null. Wir erhalten somit:
\[ A_2 = 1 – \lim_{b \rightarrow \infty} \Big( \frac{1}{b} \Big) = 1 – 0 = \underline{\;1\;} \]
Die Fläche \(A_2\) ist unendlich breit und doch ist sie endlich, nämlich 1. Beachte, dass wir hier eine analoge Situation zu den unendlichen Reihen haben, insbesondere zur harmonischen Reihe.
Uneigentliche Integrale haben mindenstens eine Integrationsgrenze, die \(+\infty\) oder \(-\infty\) ist. Uneigentliche Integrale sind konvergent oder divergent. Für die Berechnung uneigentlicher Integrale wird die betreffende Grenze mit einem Grenzwert berechnet:
\[ \int_a^{\infty} f(x) \; dx \;\; = \;\; \lim_{b \rightarrow \infty} \Big( \int_a^b f(x) \; dx \Big) \]
\[ \int_{-\infty}^b f(x) \; dx \;\; = \;\; \lim_{a \rightarrow -\infty} \Big( \int_a^b f(x) \; dx \Big) \]
Wenn beide Integrationsgrenzen unendlich sind, muss das Integral an einer geeigneten Stelle \(b\) aufgeteilt werden. Damit erhalten wir zwei Integrale mit je einer Integrationsgrenze, für die der Grenzwert gebildet wird.
\[ \int_{-\infty}^{\infty} f(x) \; dx \;\; = \;\; \lim_{a \rightarrow -\infty} \Big( \int_a^b f(x) \; dx \Big) + \lim_{c \rightarrow \infty} \Big( \int_b^c f(x) \; dx \Big) \]
Beispiel
Berechne das folgende Integral:
\[ A = \int_1^{\infty} x \; dx \]
Die Fläche \(A\) ist die Fläche unter der 45°-Geraden ab der Stelle \(x=1\). Für \(x \rightarrow \infty\) wächst die Funktion auch ins Unendliche. Die Fläche sollte unendlich sein.
\[ A = \lim_{b \rightarrow \infty} \Big ( \int_1^b x \; dx \Big) \]
\[ = \lim_{b \rightarrow \infty} \Big ( \big[ \frac{1}{2} x^2 \big]_1^b \Big) \]
\[ = \lim_{b \rightarrow \infty} \Big ( \frac{1}{2} b^2 – \frac{1}{2} \Big) \]
\[ = \lim_{b \rightarrow \infty} \Big ( \frac{1}{2} b^2 \Big) – \lim_{b \rightarrow \infty} \Big (\frac{1}{2} \Big) \]
\[ A = \lim_{b \rightarrow \infty} \Big ( \frac{1}{2} b^2 \Big) – \frac{1}{2} \rightarrow \infty \]
Der erste Grenzwert über \(b^2\) divergiert. Wenn \(b\) unendlich gross wird, wird \(b^2\) erst recht gross, d.h. wird ebenfalls unendlich. Das Integral ist divergent.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.