Die Produktregel wird benötigt, wenn ein Produkt von zwei Teilfunktionen abgeleitet werden soll. Wir haben bisher auch schon Produkte abgeleitet, jedoch waren das Produkte mit Faktoren, die nicht von der Ableitungsvariablen abhängen. Wir sprechen in diesem Fall von konstanten Faktoren bzw. Konstanten und benutzen die Faktorregel. Beispiele für Funktionen, die mit der Faktorregel abgeleitet werden:
\[ f_1(x)=2\cdot x \]
\[ f_2(x)=x^2\cdot t \]
\[ f_3(x)=e^x\cdot \sin(t) \]
Beachten Sie, dass \(2\) selbstverständlich eine Konstante ist. \(t\) und \(\sin(t)\) sind streng genommen keine Konstanten, jedoch ändern sie sich mit \(t\) und nicht mit \(x\). Wenn wir die Funktionen nach \(x\) ableiten, nehmen wir an, dass \(t\) konstant bleibt.
Wenn das Produkt aus zwei Teilfunktionen besteht, die beide von der Ableitungsvariablen (z.B. \(x\)) abhängen, dann müssen wir die Produktregel anwenden. Beispiele für solche Funktionen sind:
\[ f_4(x)=u(x)\cdot v(x) \]
\[ f_5(x)=x^2\cdot e^{-x} \]
\[ f_6(x)=2x^3\cdot \sin(x) \]
Können wir die Produktregel vielleicht erraten? Vielleicht ist sie so wie die Summenregel: Die Ableitung eines Produkts ist vielleicht gleich dem Produkt der Ableitungen? Wir probieren es an einem Beispiel aus:
\[ f(x)=x^4 = \big(x^2 \cdot x^2\big) \]
\[ f'(x) \stackrel{?}{=} \frac{d}{dx}\big(x^2\big) \cdot \frac{d}{dx}\big(x^2\big) \]
Wir kennen die Lösung:
\[ f'(x)=\frac{d}{dx}\big(x^4\big) = 4x^3 \]
Wenn wir die Teilfunktionen ableiten, erhalten wir aber:
\[ \frac{d}{dx}\big(x^2\big) \cdot \frac{d}{dx}\big(x^2\big) = 2x \cdot 2x = 4x^2 \quad \neq \quad f'(x) \]
Es hat nicht funktioniert! Die Produktregel ist offenbar anders aufgebaut als die Summenregel.
Herleitung mit Hilfe einer Linearisierung
Um die richtige Produktregel zu finden, stellen wir den Differentialquotienten auf:
\[ f'(x)=\lim_{\Delta x \rightarrow 0}\Bigg(\frac{f(x+\Delta x) – f(x)}{\Delta x}\Bigg) \]
Für die Funktion \(f\) haben wir jetzt ein Produkt von zwei Teilfunktionen \(u(x)\) und \(v(x)\):
\[ f(x)=u(x)\cdot v(x) \]
\[ f'(x)=\lim_{\Delta x \rightarrow 0}\Bigg(\frac{u(x+\Delta x) \cdot v(x+\Delta x) – u(x) \cdot v(x)}{\Delta x}\Bigg) \]
Für die Ausdrücke \(u(x + \Delta x)\) und \(v(x + \Delta x)\) wenden wir einen Trick an. Wir linearisieren die Funktion an der Stelle \(x\), d.h. wir ersetzen die Funktion \(u(x)\) und \(v(x)\) durch eine lineare Funktion, die durch den gleichen Punkt geht und die gleiche Steigung in \(x\) hat. Solange wir uns nicht zu weit von der Stelle \(x\) entfernen, fällt die Tatsache, dass wir “nur” eine Gerade haben, nicht ins Gewicht.
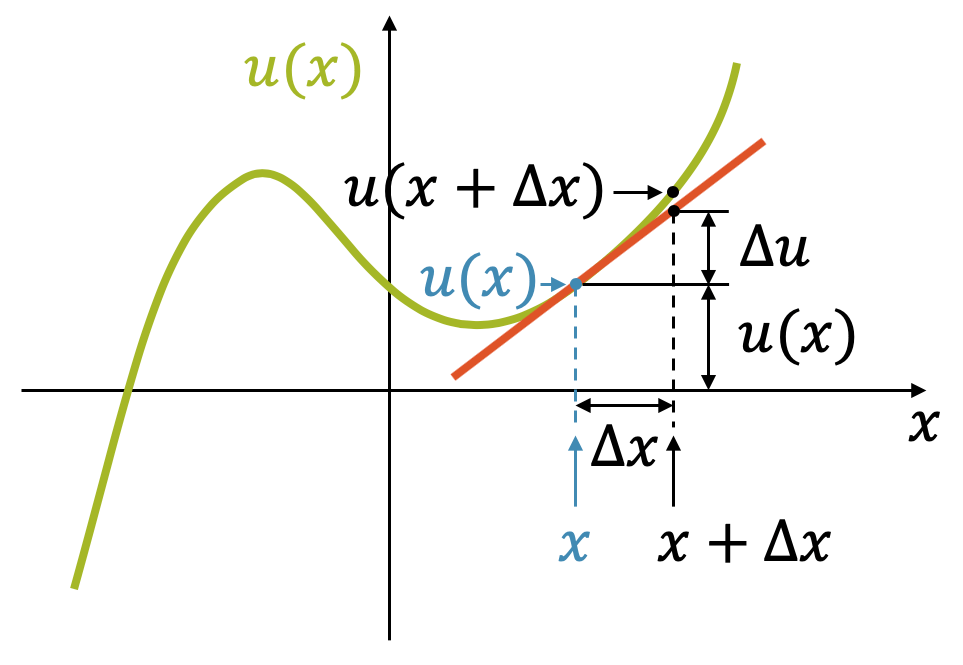
Es gilt:
\[ u(x + \Delta x) \;\; \approx \;\; u(x) + \Delta u \]
Mit Hilfe des Steigungsdreiecks haben wir für \(\Delta u\) einen Ausdruck, der die erste Ableitung (Steigung) von \(u(x)\) enthält:
\[ u'(x) = \lim_{\Delta x \rightarrow 0} \Big( \frac{\Delta u}{\Delta x} \Big) \]
\[ \rightarrow \Delta u \;\; \approx \;\; u'(x) \cdot \Delta x \]
Nun setzen wir diesen Ausdruck in den oberen Ausdruck für \(u(x + \Delta x)\) ein; analog auch die Linearisierung von \(v(x)\):
\[ u(x + \Delta x) \approx u(x) + u'(x) \cdot \Delta x \]
\[ v(x + \Delta x) \approx v(x) + v'(x) \cdot \Delta x \]
Diese beiden Ausdrücke setzen wir in den Differentialquotienten ein:
\[ f'(x)=\lim_{\Delta x \rightarrow 0}\Bigg(\frac{u(x+\Delta x) \cdot v(x+\Delta x) – u(x) \cdot v(x)}{\Delta x}\Bigg) \]
\[ = \lim_{\Delta x \rightarrow 0}\Bigg(\frac{\big(u(x) + u'(x) \cdot \Delta x \big) \cdot \big(v(x) + v'(x) \cdot \Delta x \big) – u(x) \cdot v(x)}{\Delta x}\Bigg) \]
Um die Lesbarkeit wieder etwas zurückzugewinnen, schreiben wir vorderhand nur \(u\) statt \(u(x)\) und multiplizieren dann aus:
\[ = \lim_{\Delta x \rightarrow 0}\Bigg(\frac{\big(u + u’ \Delta x \big) \cdot \big(v + v’ \Delta x \big) – uv}{\Delta x}\Bigg) \]
\[ = \lim_{\Delta x \rightarrow 0}\Bigg(\frac{uv + u v’ \Delta x + u’ \Delta x v + u’ v’ \Delta x^2 – uv}{\Delta x}\Bigg) \]
Der erste und der letzte Term im Zähler heben sich gegenseitig auf. Den Term mit dem Quadrat von \(\Delta x\) streichen wir heraus, da er viel kleiner ist als die anderen Terme im Zähler. In einem weiteren Schritt kürzen wir \(\Delta x\).
\[ \require{cancel} = \lim_{\Delta x \rightarrow 0}\Bigg(\frac{\cancel{uv}+uv’ \Delta x+u’v\Delta x+u’v’ \cancel{\Delta x^2}-\cancel{uv}}{\Delta x}\Bigg) \]
\[ \require{cancel} = \lim_{\Delta x \rightarrow 0}\Bigg(\frac{uv’ \cancel{\Delta x} + u’v \cancel{\Delta x}}{ \cancel{\Delta x} }\Bigg) \]
und erhalten schliesslich den Ausdruck:
\[ f'(x) = uv’+u’v \]
Die erste Ableitung eines Produkts von zwei Teilfunktionen wird mit der Produktregel berechnet:
\[ f(x) = u(x) \cdot v(x) \]
\[ \rightarrow f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x) \]
Beachte, dass die Produktregel angewandt werden muss, wenn es sich um ein Produkt von zwei Ausdrücken handelt, die beide von \(x\) abhängig sind. In unserem Beispiel waren das \(u(x)\) und \(v(x)\). Anders ist das, wenn z.B. der erste Ausdruck nicht von \(x\) abhängig ist, also \(u\) statt \(u(x)\)…oder eben \(c\): Die Funktion, die wir ableiten ist dann \(f(x) = c \cdot v(x)\). Man spricht dann von einem (konstanten) Faktor \(c\) und wendet die Faktorregel an!
Beispiel
Berechne die erste Ableitungsfunktion der Funktion
\[ f(x)=x^2 e^{-x} \]
Wir schreiben zuerst die Teilfunktionen und deren Ableitungen auf:
\[ u(x)=x^2 \quad \rightarrow \quad u'(x)=2x \]
\[ v(x)=e^{-x} \quad \rightarrow \quad v'(x)=-e^{-x} \]
Jetzt setzen wir in die Produktregel ein und erhalten so die Ableitungsfunktion:
\[ f'(x) = u’v + uv’ = 2x e^{-x} + x^2 (-e^{-x}) \]
\[ f'(x) = \underline{x e^{-x} \big(2-x\big)} \]
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.