Die zweite Ableitungsfunktion \(f”(x)\) von \(f\) wird mit einem zweiten Strich markiert. Sie ist gewissermassen die Steigung der Steigung der Funktion. Wenn eine Funktion eine positive Steigung hat, dann geht sie nach oben. Wenn diese Steigung zunimmt, dann wird es steiler. Eine positive Steigung der Steigung bedeutet, dass die Steigung immer grösser wird. Der Verlauf von \(f(x)\) ist in so einem Fall nach oben gekrümmt. Das ist bei unserer Parabel tatsächlich der Fall.
In diesem einfachen Beispiel hat uns die zweite Ableitung nur gesagt, was wir schon wussten. Bei einer unbekannnten Funktion hätten wir jetzt aber die Information über ihre Krümmung.
Wir berechnen jetzt die dritte Ableitung:
\[ f”'(x) = \lim_{\Delta x \rightarrow 0}\Big(\frac{f”(x+\Delta x)-f”(x)}{\Delta x}\Big) \]
\[ = \lim_{\Delta x \rightarrow 0}\Big(\frac{\frac{1}{2}-\frac{1}{2}}{\Delta x}\Big) = 0 \]
Wie können wir das interpretieren? Nun, die dritte Ableitung ist die Veränderung der Krümmung mit \(x\). Weil sie null ist, heisst das, sie verändert sich nicht. Die Funktion \(f\) hat gewissermassen eine konstante Krümmung. Wir können uns das nicht unbedingt genau vorstellen, denn wir vergleichen die Krümmung mit der Stelle \(x\) auf der gerade \(x\)-Achse.
Können wir die Funktion noch weiter ableiten? Ja, aber es bringt nichts mehr, denn schon der Wert \(\frac{1}{2}\) war konstant und hatte “keine Steigung” mehr. Ab null werden wir immer null kriegen, denn es ist eine konstante Zahl, die unabhängig von \(x\) ist. Bei anderen Funktionen ist es aber durchaus möglich, noch weiter abzuleiten.
Alternative Schreibweise mit dem Ableitungsoperator \(\frac{d}{dx}\):
\[ f(x) = \frac{1}{4}x^2 \]
\[ f'(x) = \frac{d}{dx}f(x) = \frac{1}{2}x \]
\[ f”(x) = \frac{d}{dx}f'(x) = \frac{d}{dx}\Big(\frac{d}{dx}f(x)\Big) \]
\[ = \frac{d^2}{dx^2}f(x) = \frac{1}{2} \]
\[ f”'(x) = \frac{d^3}{dx^3}f(x) = 0 \]
Für noch höhere \(n\)-te Ableitungen schreiben wir ein \((n)\) im Exponenten, statt \(n\) Apostrophe zu setzen. In unserem Beispiel sind diese alle null:
\[ f^{(n)}(x) = \frac{d^n}{dx^n}f(x) = 0 \]
Erste Ableitung: \(f'(x)\) ist die Steigung von \(f\)
\(f'(x)=0\) gibt uns die Minima oder Maxima von \(f\)
Zweite Ableitung: \(f”(x)\) ist die Krümmung von \(f\)
\(f”(x)=0\) gibt uns die Wendepunkte von \(f\)
Beispiel
Finden Sie für die folgende Funktion die Minima, Maxima und Wendepunkte.
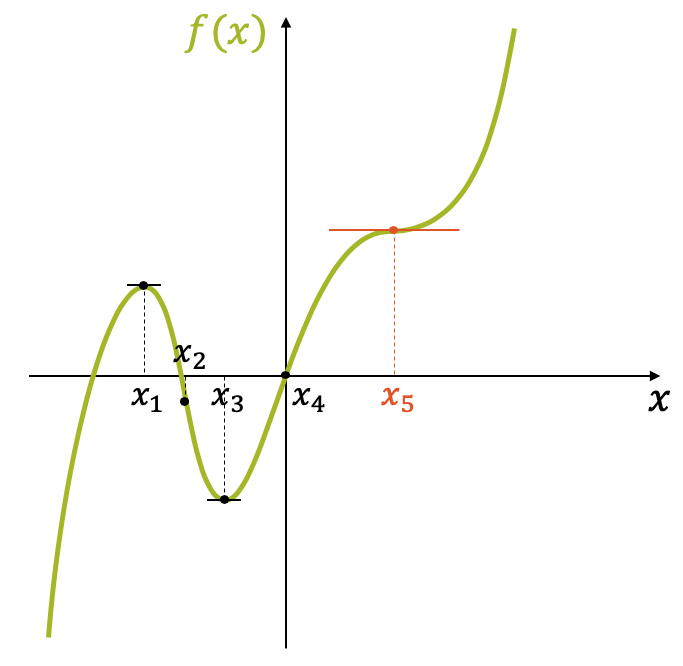
Wenn wir die erste Ableitungsfunktion auf null setzen, erhalten wir drei Extrema (keine Steigung):
\[ f'(x)\stackrel{!}{=}0 \quad \rightarrow \quad \Big \{ x_1,\;x_3,\;x_5 \Big \} \]
Die erste Ableitungsfunktion sagt uns nicht, ob es sich um Minima oder Maxima handelt, sondern nur, dass an diesen Stellen die Steigung null ist.
Wir nehmen dann die zweite Ableitung und setzen sie ebenfalls null:
\[ f”(x)\stackrel{!}{=}0 \quad \rightarrow \quad \Big \{ x_2,\,x_4,\;x_5 \Big \} \]
Hier kriegen wir die Stellen, in welchen die Funktion Wendepunkte hat (keine Krümmung).
Es fällt nun auf, dass wir an der Stelle \(x_5\) sowohl eine verschwindende Steigung, als auch eine verschwindende Krümmung haben:
\[ f'(x_5) = f”(x_5) = 0 \]
Das ist ein Spezialfall. Es handelt sich hier weder um ein Minimum, noch um ein Maximum, sondern um einen Sattelpunkt.
Wenn \(f'(x)=0\) und \(f”(x)=0\), dann handelt es sich an der Stelle \(x\) um einen Sattelpunkt.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.