In vielen Anwendungen ist es besser, das Quadrat des Funktionswerts zu nehmen, als einfach nur den Funktionswert. Nach der Summenbildung korrigieren wir das Quadrieren wieder, indem wir die Wurzel ziehen. Diese Methode wird vor allem in folgenden Fällen angewendet:
- In der Physik (z.B. Elektrotechnik) bei quadratisch wirkenden Grössen
- In der Geometrie, z.B. wenn es mehr um die Flächen, als um die Höhen doer Längen geht.
- Wenn es um die Abweichungen vom Nullwert geht, egal ob positiv oder negativ, d.h. wenn z.B. +10 und -10 einfach als 10 gewertet werden soll.
Wir schauen uns wieder die Zahlenfolge \(f_i\) an, interessieren uns dieses Mal aber für die Quadrate und stellen dies mit Quadratflächen, statt mit Säulenhöhen dar. Mit dem quadratischen Mittelwert suchen wir die Grösse \(\overline{f}\), deren Quadrat der durchschnittlichen Fläche aller Quadratflächen der Folge entspricht:
\[ 5^2, 6^2, 7^2, 6^2, 5^2, 6^2, 7^2, 6^2, … \]
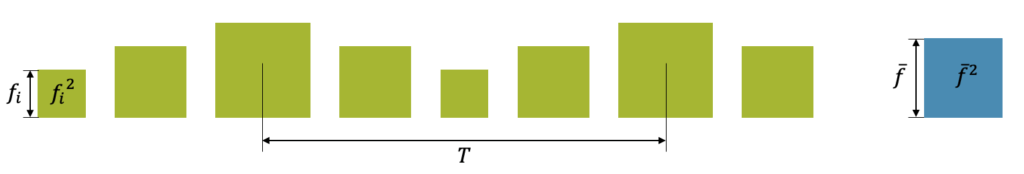
Der quadratische Mittelwert beträgt (über eine Periode gerechnet):
\[ \overline{f}_{\text{quad}} = \sqrt{\frac{5^2+6^2+7^2+6^2}{4}} \]
\[ = \sqrt{\frac{146}{4}} = 6.042 \]
Der quadratische Mittelwert ist leicht grösser als der lineare Mittelwert, der ja genau \(6\) war, weil die grossen Flächen etwas stärker gewichtet werden, als die Kleinen.
Der quadatische Mittelwert einer periodischen Funktion \(f(t)\) mit Periode \(T\) ist:
\[ \overline{f}_{\text{quad}} = \sqrt{\frac{1}{T} \int_a^{a+T} f^2(t)\;dt} \]
Wobei \(a\) eine beliebige Stelle auf der \(t\)-Achse sein kann. Gleiches gilt natürlich auch für Funktionen \(g(x)\) auf der \(x\)-Achse.
Für nicht-periodische Funktionen rechnen wir den Mittelwert im betrachteten Intervall \([a,b]\):
\[ \overline{f}_{\text{quad}} = \sqrt{\frac{1}{(b-a)} \int_a^b f^2(x)\;dx} \]
Beispiel
In der Elektrotechnik geben wir für die Wechselspannung den sog. Effektivwert an. Es handelt sich hierbei um den quadratischen Mittelwert einer Sinusfunktion.
Bestimme die Amplitude der Wechselspannung für unsere Steckdose mit \(U_{eff}=230\;\text{V}\).
Wir haben hier den quadratischen Mittelwert gegeben und müssen zurückrechnen, welche Amplitude die Sinusfunktion ursprünglich hatte.
\[ U_{eff} = \sqrt{\frac{1}{T} \int_0^T U^2(t)\;dt} \]
Für die Wechselspannung schreiben wir:
\[ U(t) = U_0 \cdot \sin(\omega t) \]
Dabei ist \(U_0\) die gesuchte Amplitude unserer Sinusfunktion und \(\omega\) die Kreisfrequenz, die mit der Periode zusammenhängt: \(T=\frac{2\pi}{\omega}\). Wir setzen das in unser Integral ein und erhalten die Gleichung, die wir nach der Unbekannten \(U_0\) auflösen müssen:
\[ U_{eff} \;\; = \;\; \sqrt{\frac{\omega}{2\pi} \int_0^{2\pi/\omega} U_0^2 \sin^2(\omega t)\;dt} \]
\[ = \sqrt{\frac{\omega}{2\pi}} \cdot U_0 \cdot \sqrt{\int_0^{2\pi/\omega} \sin^2(\omega t)\;dt} \]
\[ U_0 = \frac{U_{eff}}{\sqrt{\frac{\omega}{2\pi}} \cdot \sqrt{\int_0^{2\pi/\omega} \sin^2(\omega t)\;dt}} \]
Wir müssen zuerst mal das Integral lösen. Wir benutzen wieder die Substitution für \(\sin^2(x)\):
\[ \int_0^{2\pi/\omega} \sin^2(\omega t)\;dt = \frac{1}{2} \int_0^{2\pi/\omega} \Big(1 – \cos(2\omega t) \Big) \;dt \]
\[ = \frac{1}{2} \Big[ t – \frac{1}{2\omega}\sin(2\omega t) \Big]_0^{2\pi/\omega} \]
\[ \require{cancel} = \frac{1}{2} \Big( \frac{2\pi}{\omega} – \frac{1}{2\omega}\cancel{\sin(2\omega \cdot \frac{2\pi}{\omega})} \Big) – \frac{1}{2} \Big( \cancel{0} – \frac{1}{2\omega}\cancel{\sin(2\omega \cdot 0)} \Big) \]
\[ = \frac{\pi}{\omega} \]
Die Werte der Sinusfunktion fallen heraus, da der Sinus für \(2\pi\) und \(4\pi\) verschwindet. Jetzt haben wir das Integral gelöst und setzen seinen Wert in die Gleichung für \(U_0\) ein:
\[ \require{cancel} U_0 = \frac{U_{eff}}{\sqrt{\frac{\cancel{\omega}}{2\cancel{\pi}}} \cdot \sqrt{\frac{\cancel{\pi}}{\cancel{\omega}}}} \]
\[ = \sqrt{2} \cdot U_{eff} = \sqrt{2} \cdot 230\;\text{V} = \underline{325\;\text{V}} \]
Die Wechselspannung unserer Steckdose schwingt somit zwischen \(\pm\;\) 325V und hat damit einen quadratischen Mittelwert von \(U_{eff} =\) 230V.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.