Bei zeitlich variierenden Grössen, z.B. die Temperatur, ist es von Vorteil sie über eine bestimmte Zeit zu mitteln, z.B. die durchschnittliche Jahrestemperatur. Auf diese Art werden die Schwankungen über die betrachtete Zeitperiode ausgeglichen.
Beispiel
Die Funktion \(f(t)=A \sin^2(t)\) schwingt zwischen 0 und \(A\).
Was ist der Mittelwert \(\overline{f}\) dieser Funktion über die gesamte Zeit?
Der Mittelwert \(\overline{f}\) beschreibt die variierende Grösse \(f(t)\) dadurch, dass die blaue Fläche \(A_2\) unterhalb von \(\overline{f}\) gleich gross ist, wie die rote Fläche \(A_1\) unterhalb von \(f(t)\). Beide erzeugen über den betrachteten Zeitraum die gleiche Fläche.
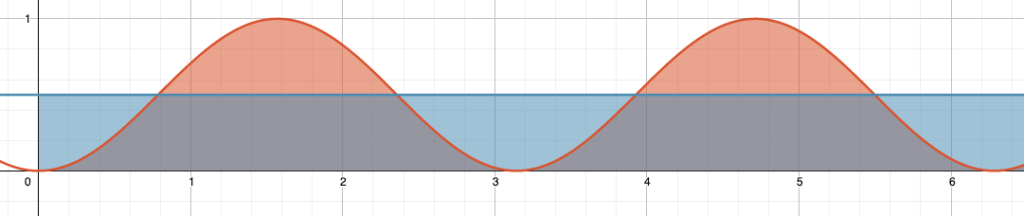
Wir werden die Frage zuerst algebraisch lösen. Für die beiden Flächen können wir schreiben:
\[ A_1 = \int_{-\infty}^{\infty} f(t)\;dt \]
\[ A_2 = \int_{-\infty}^{\infty} \overline{f}\;dt \]
Das sind uneigentliche Integrale mit unendlichen Integrationsgrenzen, d.h. beide sind unendlich und das ist ein bisschen mühsam.
Da \(f(t)\) eine periodische Funktion ist, die sich nach einer Periode wiederholt, reicht es für uns, nur eine Periode \(T\) zu betrachten. Für \(A_2\) benutzen wir zudem die Faktorregel und ziehen den konstanten Wert \(\overline{f}\) aus dem Integral heraus:
\[ A_1 = \int_0^T f(t)\;dt \]
\[ A_2 = \int_0^T \overline{f}\;dt = \overline{f} \cdot \int_0^T dt = \overline{f} \cdot T \]
Jetzt setzen wir die beiden Flächen gleich und lösen nach \(\overline{f}\) auf:
\[ \overline{f} = \frac{1}{T} \int_0^T f(t)\;dt \]
Um den Mittelwert zu erhalten, müssen wir ein Integral lösen. Wir setzen die Funktion \(f(t)=A\sin^2(t)\) und den Wert der Periode ein \(T = \pi\) ein:
\[ \overline{f} = \frac{1}{\pi} \int_0^{\pi} A \sin^2(t)\;dt = \frac{A}{\pi} \int_0^{\pi} \sin^2(t)\;dt \]
Um dieses Integral zu lösen, müssen wir zuerst das \(\sin^2(t)\) ersetzen, da es so nicht einfach lösbar ist. Man könnte es schon partiell integrieren, braucht dann aber auch einen kleinen Trick. Wir benutzen die Identität für den Kosinus eines doppelten Winkels, da in ihm das Quadrat des Sinus’ vorkommt:
\[ \cos(2t) = \cos(t)\cdot\cos(t) – \sin(t)\cdot\sin(t) \]
\[ = \cos^2(t)-\sin^2(t) \]
Jetzt ersetzen wir den \(\cos^2(t)\) mit der anderen Identität:
\[ \sin^2(t) + \cos^2(t) = 1 \]
\[ \rightarrow \quad \cos^2(t) = 1 – \sin^2(t) \]
Oben eingesetzt ergibt das:
\[ \cos(2t) = 1 – \sin^2(t) – \sin^2(t) \]
\[ \rightarrow \quad \sin^2(t) = \frac{1}{2}\big( 1 – \cos(2t) \big) \]
Jetzt schreiben wir das Integral neu und ersetzen das Quadrat des Sinus’ dem neuen Ausdruck:
\[ \overline{f} = \frac{A}{2\pi} \int_0^{\pi} \Big( 1-\cos(2t) \Big) \;dt \]
Wir lösen das Integral, indem wir eine Stammfunktion für \(1-\cos(2t)\) “erraten”. Wir schreiben sie hin, leiten sie zur Kontrolle nochmals ab und vergleichen das Resultat mit der Funktion im Integral.
\[ \frac{A}{2\pi} \int_0^{\pi} \Big( 1-\cos(2t) \Big) \;dt \]
\[ = \frac{A}{2\pi} \cdot \Big [ t – \frac{1}{2} \sin(2t) \Big ]_0^{\pi} \]
\[ \require{cancel} \frac{A}{2\pi} \cdot \Big( \pi – \frac{1}{2} \cancel{\sin(2\pi)} \Big) – \frac{A}{2\pi} \cdot \Big( \cancel{0} – \frac{1}{2} \cancel{\sin(2\cdot 0)}\Big) \]
\[ = \frac{A}{2\pi} \cdot \pi = \underline{\frac{A}{2}} \]
Dieses Resultat haben wir natürlich erwartet, denn wir können in diesem Fall die Aufgabe auch geometrisch überlegen: Die Flächen, die über dem Mittelwert liegen, passen formgerecht in die Löcher der Fläche unter dem Mittelwert.
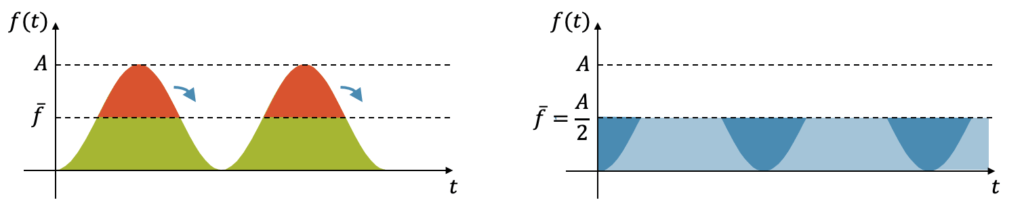
Warum heisst dieser Mittelwert linear? Nun, wir betrachten dazu eine einfache Zahlenfolge:
\[ f_i = 5, 6, 7, 6, 5, 6, 7, 6, … \]
Auch hier haben wir eine periodische Sache, d.h. der Mittelwert der Zahlenfolge lässt sich mit einer Summe der Folgeglieder über eine Periode bestimmen:
\[ \overline{f} = \frac{5+6+7+6}{4} = 6 \]
Was haben wir hier berechnet? Wir können die Zahlenfolge mit einem kleinen Säulendiagramm darstellen:
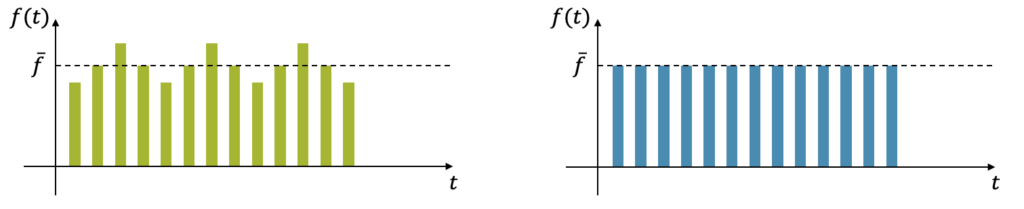
Der Mittelwert \(\overline{f}\) stellt dabei die durchschnittliche Höhe der Säulen dar. Wir haben also (eindimensionale) Längen addiert und deren Durchschnitt berechnet. Längen sind lineare Grössen und der Durchschnitt ist deshalb ein linearer Durchschnitt.
Jetzt wirst du dich vermutlich fragen, inwiefern wir in unserem ersten Beispiel von einem linearen Durchschnitt reden können, wenn wir doch Integrationsflächen betrachtet haben. Dazu gibt es zwei Erklärungen: Erstens sind Integrale nichts anderes als Summen von unendlich dünnen Säulen, d.h. mit der Berechnung des Integrals haben wir eigentlich das Gleiche getan, wie im Beispiel der Zahlenfolge. Zweitens haben wir die Fläche des Integrals, die tatsächlich quadratischer Natur ist und nicht linear, durch die Länge der Periode geteilt. Damit haben wir aus einer Fläche wieder eine Länge gemacht.
Der lineare Mittelwert einer periodischen Funktion \(f(t)\) mit Periode \(T\) ist:
\[ \overline{f}_{\text{lin}} = \frac{1}{T} \int_a^{a+T} f(t)\;dt \]
Wobei \(a\) eine beliebige Stelle auf der \(t\)-Achse sein kann. Gleiches gilt natürlich auch für Funktionen \(g(x)\) auf der \(x\)-Achse.
Für nicht-periodische Funktionen rechnen wir den Mittelwert im betrachteten Intervall \([a,b]\):
\[ \overline{f}_{\text{lin}} = \frac{1}{(b-a)} \int_a^b f(x)\;dx \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.