Zentripetalbeschleunigung

Änderung der Richtung der Geschwindigkeit

Beschleunigung ist die Änderung der Geschwindigkeit pro Zeit. Im klassischen Sinne spricht man da von “schneller werden” oder “abbremsen”. Dabei ändert sich der Betrag der Geschwindigkeit.

Mit der Definition der Beschleunigung \(a=\frac{\Delta v}{\Delta t}\) erhalten wir

\[ \Delta v = a \cdot \Delta t \]

Für \(\Delta v\) können wir auch die Differenz der Geschwindigkeit zwischen “vorher” (Zustand 0) und “nachher” (Zustand 1) einsetzen:

\[ \Delta v = v_1 – v_0 \]

Wir erhalten so:

\[ v_1 = v_0 + a \cdot \Delta t \]

Die Geschwindigkeit nach einer kurzen Zeitperiode \(\Delta t\) entspricht der ursprünglichen Geschwindigkeit \(v_0\) zuzüglich der Änderung der Geschwindigkeit \(a\Delta t\) in dieser Zeit. Die neue Geschwindigkeit heisst \(v_1\).

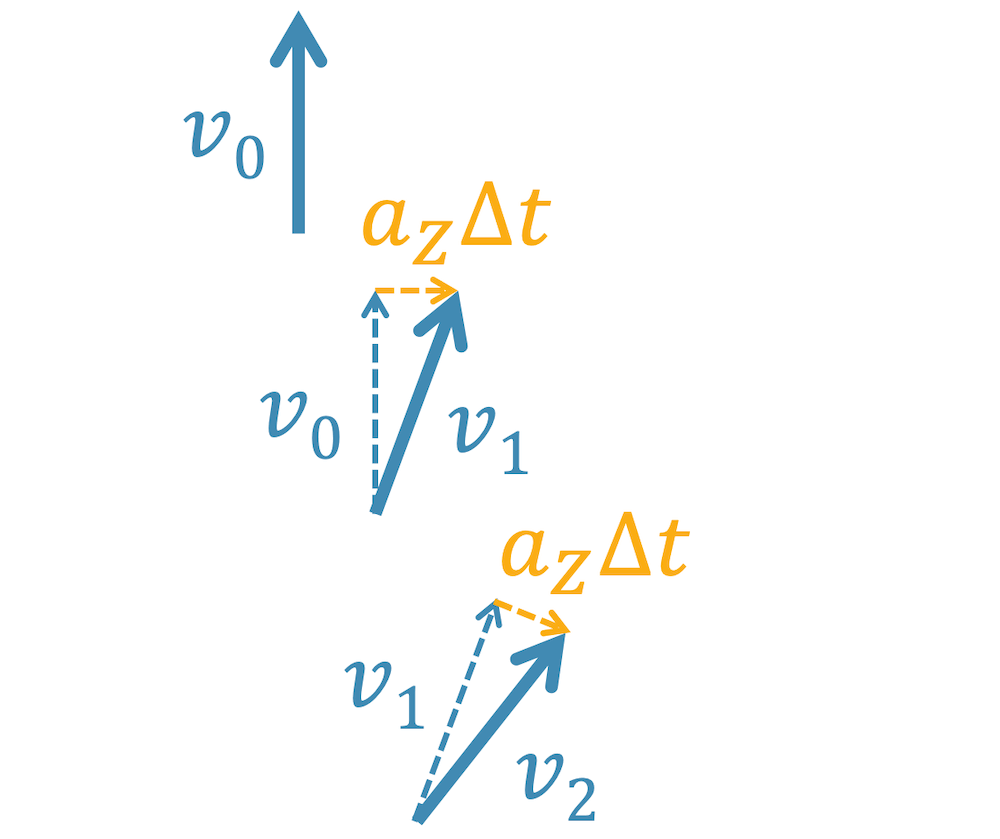
Die Geschwindigkeit ist jedoch ein Vektor und hat nebst ihrem Betrag auch eine Richtung. Wenn sich die Richtung der Geschwindigkeit ändert, ändert sich so gesehen die Geschwindigkeit auch. Der Betrag ist zwar gleich geblieben, d.h. wir zeichnen vorher und nachher einen gleich langen Pfeil. Hätten wir einen Tacho, so würde dieser immer noch den gleichen Betrag anzeigen. Es hat sich nur die Richtung der Geschwindigkeit geändert – das merkt der Tacho nicht. Auf dem Kompass würden wir die Richtungsänderung aber sehen.

Die Zentripetalbeschleunigung \(a_Z\) ist die Beschleunigung, die nur die Richtung der Geschwindigkeit ändert. Der Vektor der Zentripetalbeschleunigung steht senkrecht auf dem Geschwindigkeitsvektor. Die Zentripetalbeschleunigung vermag aus diesem Grund nicht, den Betrag der Geschwindigkeit zu vergrössern oder zu verkleinern, wie die klassische Beschleunigung \(a\).

In der obigen Grafik sehen wir, wie aus einer Geschwindigkeit \(v_0\), die senkrecht nach oben zeigt, eine Geschwindigkeit \(v_1\) und dann \(v_2\) entsteht, die zwar vom Betrag her gleich gross ist, jedoch im Uhrzeigersinn abgedreht ist. Verantwortlich für diese Änderung war die Zentripetalbeschleunigung \(a_Z\).

Zentripetalbeschleunigung im Orbit

Wenn ein Himmelskörper oder Satellit um einen anderen Himmelskörper dreht, sagt man, er sei im Orbit. Meistens ist diese Bahn elliptisch geformt. Wir betrachten der Einfachheit halber die einfachste Ellipse, die es gibt, den Kreis. Die internationale Raumstation ISS kreis um die Erde in einer Höhe von rund 400 km über dem Boden. Die Atmosphäre ist in dieser Höhe schon so unglaublich dünn, dass wir praktisch keinen Luftwiderstand mehr haben. Die ISS fliegt deshalb ungebremst mit hoher Geschwindigkeit an der Erde vorbei.

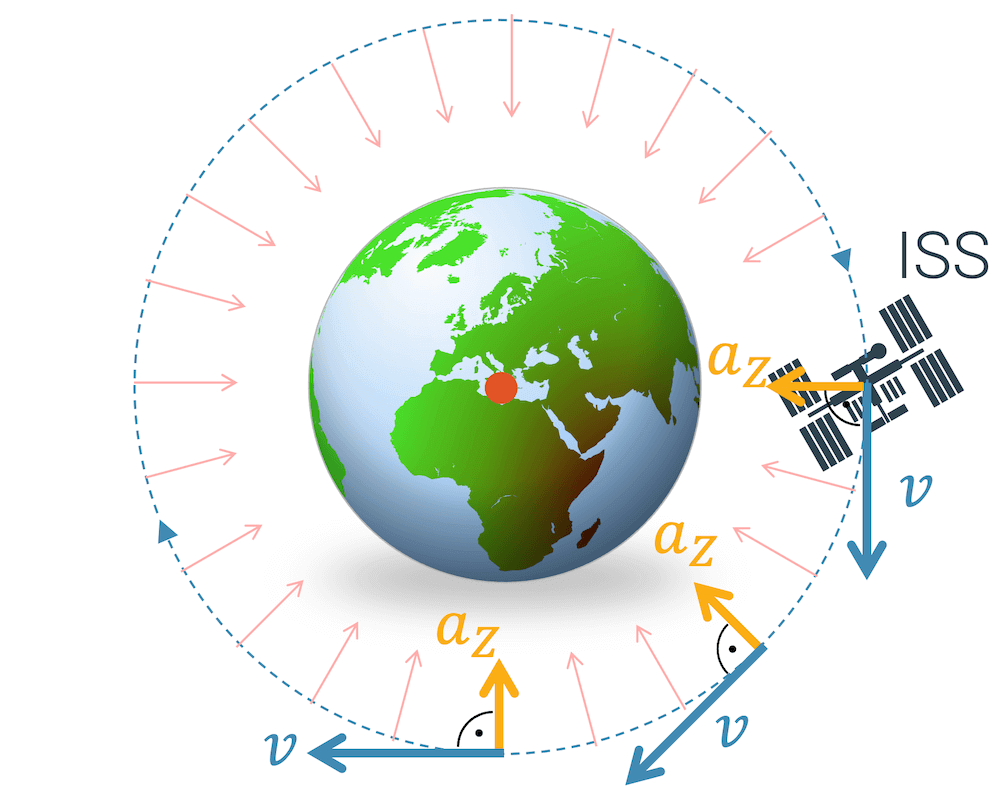
Der Grund, warum sie nicht in einer geraden Linie an uns vorbeifliegt, liegt an der Erdbeschleunigung \(g\). In der Höhe von 400 km ist diese um etwa 10% reduziert. Sie wirkt deshalb fast so stark, wie wir sie auf der Erde kennen. Die Schwerelosigkeit an Bord der ISS ist trügerisch, denn auch dort wirken rund 90% der Erdbeschleunigung \(g\).

Die Erdbeschleunigung ändert die Fluggeschwindigkeit der ISS so, dass sie dauernd ihren Kurs ändert. Dadurch entsteht die Kreisbahn der ISS um die Erde herum. Die Erdbeschleunigung wirkt als reine Zentripetalbeschleunigung, denn die ISS wird nicht schneller oder langsamer dadurch.

Anwendungsbeispiel: Zentrifugen

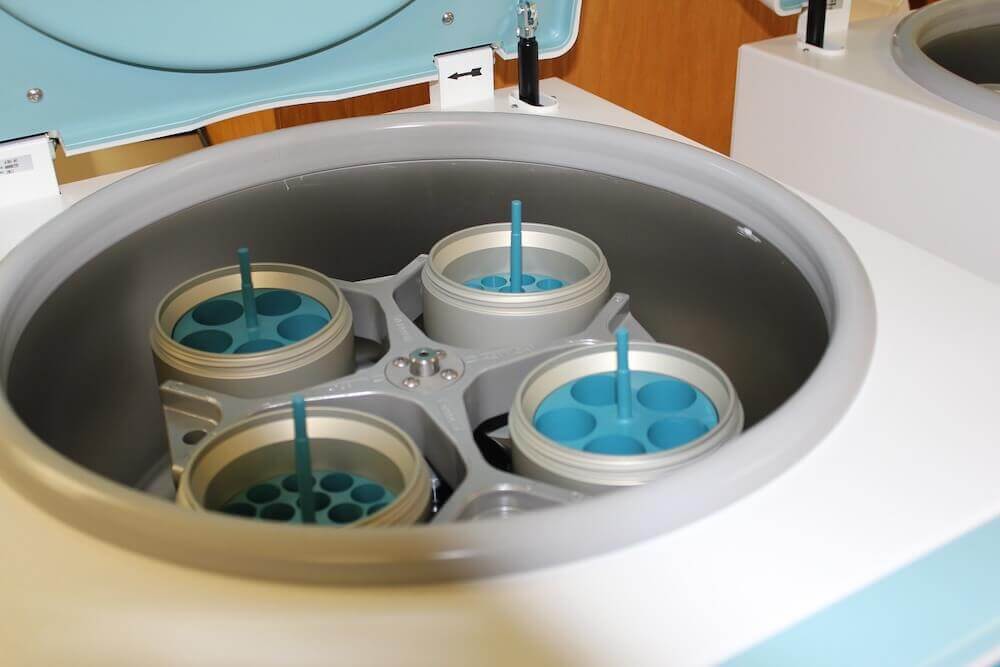
Blutproben können in Zentrifugen relativ schnell in die festen Bestandteile des Bluts (Blutzellen) und das umgebende Plasma getrennt werden. Würden wir die Probe einfach senkrecht hinstellen, würde die Erdbeschleunigung langsam eine Trennung vornehmen. In der Zentrifuge wird jedoch eine so schnelle Drehbewegung erreicht, dass die Zentripetalbeschleunigung mehr als das Tausendfache der Erdbeschleunigung erreicht! Betrachtet man das Gefäss der Blutprobe, wirkt die vom Betrag her gleich grosse, in der Richtung jedoch umgekehrte Zentrifugalbeschleunigung. Die Trennung des Bluts in die Bestandteile erfolgt damit viel ebenfalls um mehr als das Tausendfache schneller.

Berechnung der Zentripetalbeschleunigung

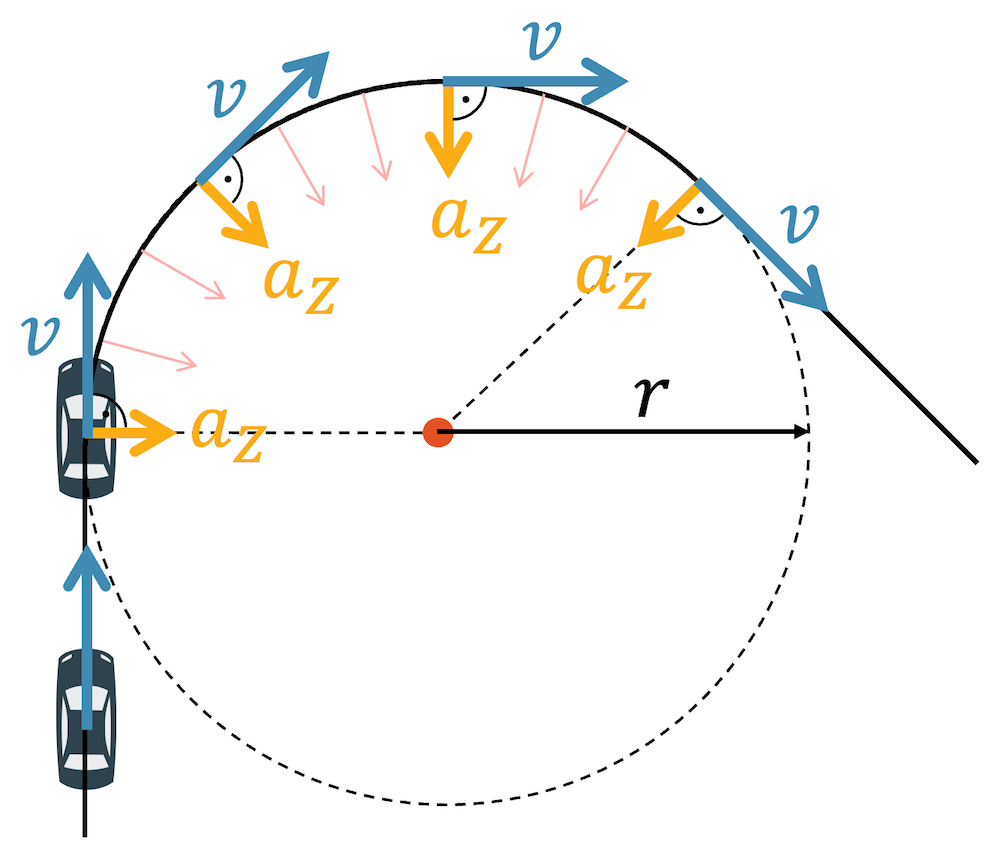
Nehmen wir ein Auto, das eine Kurve fährt, wie in der obigen Grafik. In der Umgangssprache würden wir sagen, dass das Auto mit konstanter Geschwindigkeit die Kurve abfährt. In der Physik sind wir da ein bisschen genauer und sagen, dass das Auto mit konstantem Betrag der Geschwindigkeit fährt, d.h. der Vektorpfeil der Geschwindigkeit bleibt gleich lang. Allerdings ändert sich die Richtung der Geschwindigkeit und das durch eine Zentripetalbeschleunigung \(a_Z\), die zum Zentrum des Kreises der Kurve gerichtet ist.

Beachte dabei wie ähnlich die Grafik mit dem Auto und die Zeichnung der ISS um die Erde herum, sind. Das Prinzip ist das Gleiche!

Die Zentripetalbeschleunigung \(a_Z\) ist abhängig von der Enge der Kurve und der Geschwindigkeit, mit welcher man in die Kurve fährt. Wir wissen, dass eine Kurve mit einem kleinen Radius uns eher ins Schleudern bringen wird, als eine langgezogene Kurve. Natürlich kommen wir auch ins Schleudern, wenn wir die Kurve zu schnell anfahren. Für die Zentripetalbeschleunigung gilt nämlich:

\[ a_Z = \frac{v^2}{r} \]

Je grösser die Geschwindigkeit \(v\), desto grösser wird der Bruch und damit \(a_Z\). Gleiches gilt bei sehr kleinem Radius \(r\) bei engen Kurven.

Beispiel

Zeichne die Beschleunigungsvektoren für die Bewegung des Autos in der S-Kurve.

---

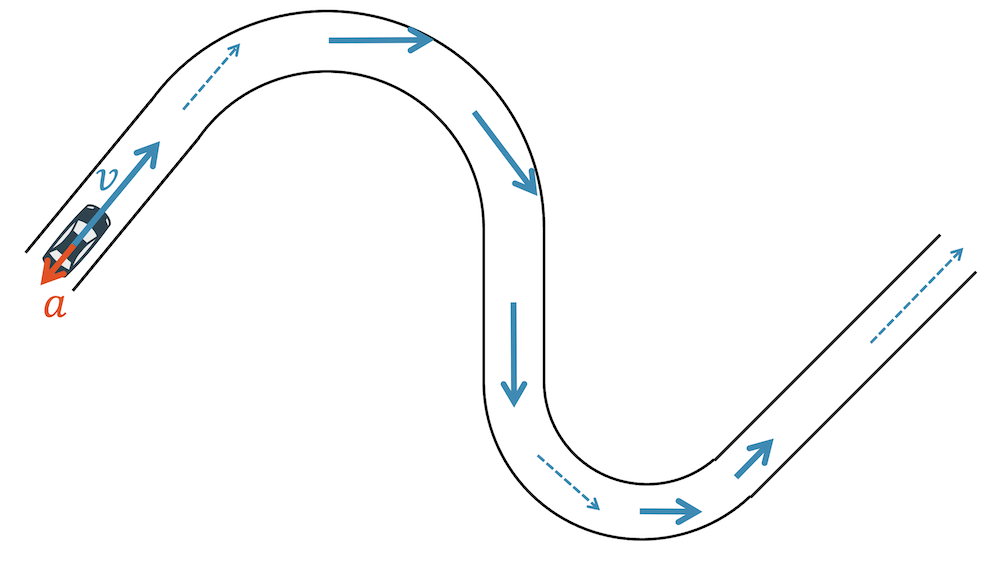
Wir schauen uns immer zwei Geschwindigkeitsvektoren an und vergleichen sie. Die Änderung vom ersten zum zweiten Pfeil gibt uns die Beschleunigung, die dazu gebraucht wird:

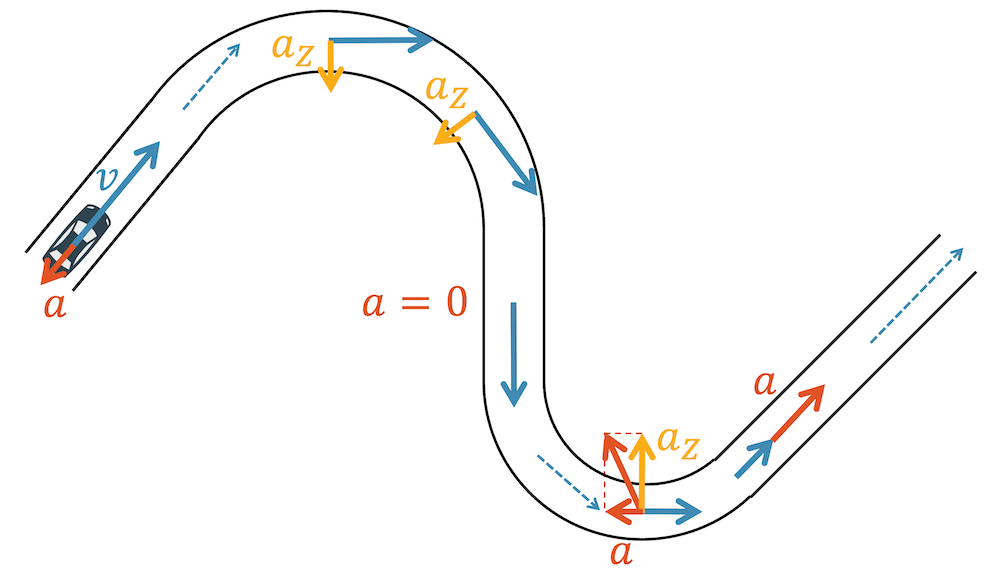
  – Der zweite Geschwindigkeitspfeil (in der Kurve) ist kürzer als der Erste. Das Auto bremst ab, so dass wir eine Beschleunigung entgegensetzt zur Geschwindigkeit haben müssen.

  – Der dritte Geschwindigkeitsvektor ist gleich lang wie der zweite Geschwindigkeitsvektor. Jedoch muss die Richtung mit Hilfe einer Zentripetalbeschleunigung \(a_Z\) (zum Zentrum der Kurve gerichtet) geändert werden.

  – Wieder die gleiche Situation. Wir brauchen nochmals eine Zentripetalbeschleunigung, um die Kurve zu machen.

  – Auf dem geraden Stück ändert sich die Geschwindigkeit weder in Betrag, noch in der Richtung. Die Beschleunigung verschwindet: \(a=0\)

  – In der Linkskurve wird abgebremst (die Pfeile werden kürzer) und die Richtung geändert. Es braucht deshalb beide Arten von Beschleunigung (Abbremsen + Zentripetalbeschleunigung). Beide Beschleunigungen werden als Vektor addiert. Es resultiert eine Beschleunigung, die in die Kurve, aber nicht zum Zentrum, sondern etwas nach hinten gerichtet ist.

  – Auf dem geraden Stück wird wieder beschleunigt. die Beschleunigung ist mit der Geschwindigkeit gleich gerichtet.