Beschleunigungs-Zeit-Diagramm (a-t-Diagramm)

Steigung im v-t-Diagramm

Du kannst dich vielleicht erinnern, dass wir im s-t-Diagramm gesagt haben, dass die Geschwindigkeit \(v\) als Steigung abgelesen werden kann, denn wir haben ein Steigungsdreieck mit einer vertikalen Kathete der Länge \(\Delta s\) und einer horizontalen Kathete der Länge \(\Delta t\):

\[v=\frac{\Delta s}{\Delta t}\]

Jetzt übertragen wir dies auf das v-t-Diagramm und stellen fest, dass das Steigungsdreieck der Definition der Beschleunigung \(a\) entspricht, denn es gilt:

\[a=\frac{\Delta v}{\Delta t}\]

Wir könnten deshalb die Beschleunigung als Steigung im v-t-Diagramm ablesen.

Aus der Steigung eines s-t-Diagramms haben wir die Geschwindigkeit erhalten, was zum v-t-Diagramm führt. Aus der Steigung eines v-t-Diagramms erhalten wir die Beschleunigung, was zum a-t-Diagramm führt! 😮

Erstellen eines a-t-Diagramms

Für die Erstellung eines a-t-Diagramms brauchen wir also ein v-t-Diagramm, indem wir die gleichen Regeln anwenden, wie damals von einem s-t-Diagramm zu einem v-t-Diagramm:

• Die Steigung im s-t-Diagramm entspricht der Geschwindigkeit \(v\), die wir als Höhe im v-t-Diagramm abtragen
• Die Steigung im v-t-Diagramm entspricht der Beschleunigung \(a\), die wir als Höhe im a-t-Diagramm abtragen

Schauen wir uns das folgende Beispiel an: Das s-t-Diagramm der Bewegung sei gegeben. Wir haben die Bewegung im s,t-Diagramm in drei zeitliche Abschnitte A, B und C aufgeteilt:

• Im ersten zeitlichen Abschnitt A nimmt die Steigung zu (nach oben gekrümmt)
• Im zweiten Abschnitt B ist die Steigung konstant positiv (gerade)
• Im dritten Abschnitt C nimmt die Steigung wieder ab (nach unten gekrümmt)

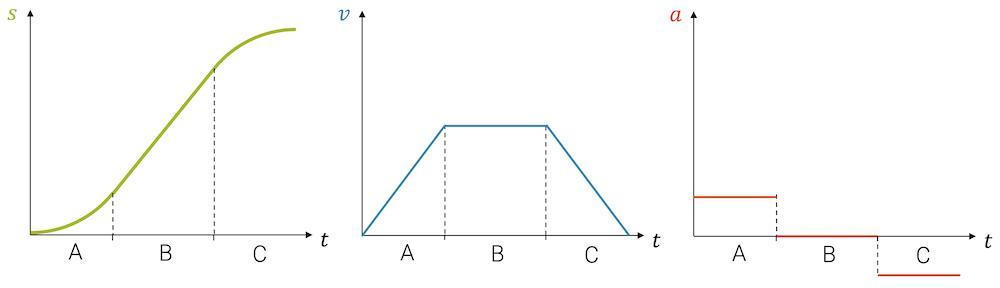
Im Abschnitt A startet die Geschwindigkeit bei null und nimmt zu. Wir haben also eine Zunahme der Geschwindigkeit von null bis zu einem bestimmten Wert.

Im Abschnitt B ist die Steigung im s-t-Diagramm konstant, d.h. sie ändert sich nicht und dadurch ändert sich auch die Geschwindigkeit nicht: Sie bleibt konstant.

Schliesslich nimmt die Geschwindigkeit im Abschnitt C wieder ab, bis sie null ist. Im v-t-Diagramm haben wir deshalb eine zunehmende (A), konstant gehaltene (B) und dann wieder abnehmende Geschwindigkeit (C).

Nun konstruieren wir das a-t-Diagramm und schauen dazu das v-t-Diagramm an. Wir sehen, dass im Abschnitt A wir eine konstant positive Steigung der Geschwindigkeit haben. Das gibt uns einen konstant positiven Wert für die Beschleunigung. Im Abschnitt B muss die Beschleunigung null sein, da die Geschwindigkeit sich nicht ändert. Schliesslich haben wir eine konstante negative Steigung der Geschwindigkeit im Abschnitt C, d.h. die Beschleunigung ist konstant negativ.

Wir erhalten in diesem Beispiel für das a-t-Diagramm einen stufenförmigen Verlauf.

a-t-Diagramm bei gleichmässig beschleunigter Bewegung

Wie sieht die Bewegung aus, wenn wir in einem Fahrzeug einfach immer gleich viel “Gas geben”? Unter der Annahme, dass die Kraft auf unser Fahrzeug schön konstant bleibt, haben wir gemäss Newtons Zweitem Gesetz eine ebenfalls konstante Beschleunigung.

Sie ist die Steigung der Geschwindigkeit im v-t-Diagramm, d.h. dort sollten wir eine konstante Steigung haben bzw. einen linearen Verlauf.

Im s-t-Diagramm bildet sich eine halbe Parabel. Ihr Steigungen nehmen linear zu.

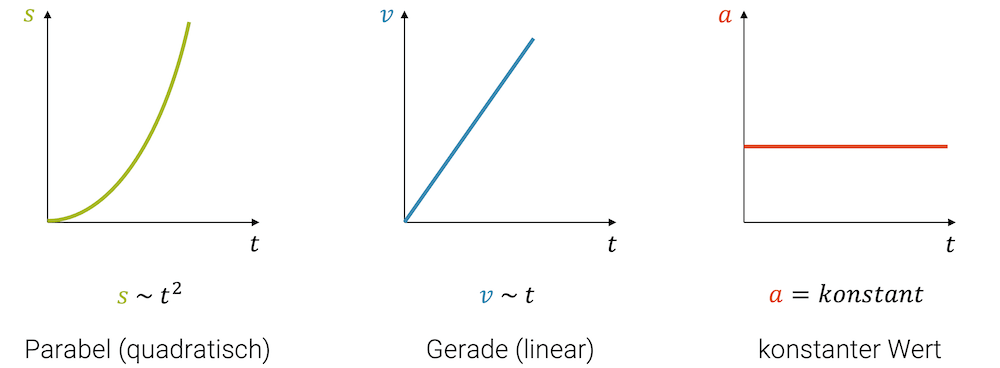
Die drei Diagramme gehören zur sog. gleichmässig beschleunigten Bewegung oder einfach zu einer Bewegung mit konstanter Beschleunigung. Auch wenn sie nach einem Spezialfall aussieht, so kommt diese spezielle Form der Bewegung sehr oft vor, z.B. beim freien Fall, wo die Beschleunigung konstant ist, nämlich die Fall- oder Erdbeschleunigung. 👀

Nachfolgend siehst du drei gemessene Diagramme für die Bewegung eines kleinen Fahrzeugs, das von einer Masse angetrieben wird, die sich im freien Fall befindet. Wir erkennen, dass die Verläufe weitgehend den theoretischen Voraussagen von oben entsprechen. Die Beschleunigung ist einigermassen konstant und erzeugt einen linearen Verlauf bei der Geschwindigkeit und einen parabelförmigen Verlauf im s-t-Diagramm.

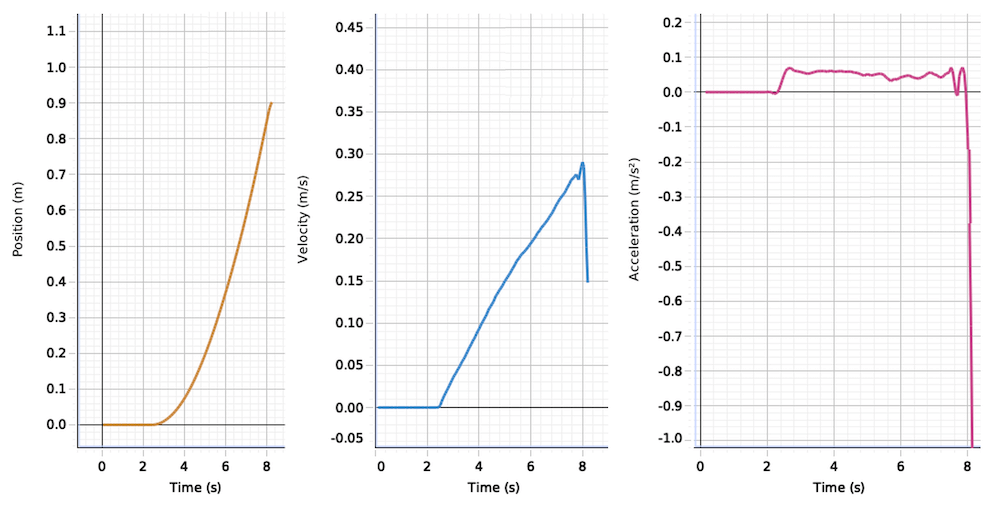
Ganz am Schluss sehen wir einen plötzlichen Zusammenbruch der Geschwindigkeit und eine entsprechend stark negative Beschleunigung. Das ist der Zeitpunkt, bei welchem das bewegte Objekt am Ende der Schiene in den Puffer rammt.

Darstellung einer Geschwindigkeit im a-t-Diagramm

Wir hatten damals gesehen, dass im v-t-Diagramm die Fläche zwischen dem Verlauf und der t-Achse einer Strecke entspricht. Am besten erkennt man dies an den Einheiten, wenn wir im Diagramm die Höhe \(\Delta v\) und die Breite \(\Delta t\) eines Rechtecks multiplizieren:

\[ \Delta v \cdot \Delta t = \frac{\text{m}}{\text{s}} \cdot \text{s} = \text{m} \]

In analoger Weise ist eine Fläche im a-t-Diagramm eine Geschwindigkeit und zwar die mittlere Geschwindigkeit für den betrachteten Zeitraum:

\[ \Delta a \cdot \Delta t = \frac{\text{m}}{\text{s}^2} \cdot \text{s} = \frac{\text{m}}{\text{s}} \]

Im a-t-Diagramm entspricht die Fläche unter dem Bewegungsverlauf der (mittleren) Geschwindigkeit.