Impuls

Definitionen 

Abkürzung: \(\;\;\vec{p} \;\;\) bzw. \(\;\; p\)

Einheit: \(\;\;[\,p\,] = \frac{\text{kg m}}{\text{s}}\)

Impuls ist eine abstrakte Grösse wie die kinetische Energie. Körper mit Masse und einer Geschwindigkeit haben nicht nur kinetische Energie, sondern auch Impuls. Die kinetische Energie selbst ist keine Erhaltungsgrösse, denn sie kann in eine andere Energieform umgewandelt werden. Beim Impuls gibt es keine andere Form. Der Impuls ist eine Erhaltungsgrösse. Er kann zwar zu- oder abgeführt werden. Wenn das System aber als abgeschlossen gilt, können wir davon ausgehen, dass der Impuls mit Betrag und Richtung erhalten bleibt.

Der Impuls \(\vec{p}\) ist definiert als Produkt von Masse \(m\) und Geschwindigkeit \(\vec{v}\). Er hat die gleiche Richtung, wie die Geschwindigkeit.

\[ \vec{p} = m \cdot \vec{v} \]

Für den Betrag des Impulses gilt entsprechend:

\[ p = m \cdot v \]

Kraftstoss 

Der Impuls ist eine Erhaltungsgrösse, die Betrag und Richtung beibehält. Wenn das immer so gelten würde, dann könnten wir z.B. mit dem Velo nie losfahren oder abbremsen. Die Erhaltung des Impulses gilt nur für ein abgeschlossenes System, das von aussen keiner Kraft ausgesetzt ist. In unserem Beispiel behält das Velo seinen Impuls bei, solange keine Kraft einwirkt. Das erinnert uns doch stark an Newtons Erstem Gesetz, das besagt, dass ein Körper seine Geschwindigkeit (und Masse) konstant beibehält, wenn keine Kraft auf ihn wirkt.

Wenn wir einen Gegenstand beschleunigen wollen, dann braucht es eben eine Kraft, wie das uns Newtons Zweites Gesetz gelehrt hat. Wenn eine Kraft \(F\) eine gewisse Zeit \(\Delta t\) auf einen Gegenstand einwirkt, dann wird sich der Impuls \(p\) verändern. Wir nennen diese Änderung des Impulses \(\Delta p\): Sie ist positiv, wenn der Impuls zunimmt und negativ, wenn er abnimmt. Damit erhält die Kraft eine neue Interpretation: Sie ist die Impulsänderung pro Zeit.

Gewisse Physiker sprechen statt von Kraft auch von Impulsstrom, d.h. als würde diese abstrakte Grösse “fliessen”. Ich finde das ein bisschen zu abstrakt. An dem Begriff gefällt mir aber, dass die Einwirkungszeit besser zur Geltung kommt. Je länger ein Gegenstand einer Kraft ausgesetzt ist, desto mehr Impuls kann in ihn “ein- bzw. ausströmen” und er wird entsprechend seinen Impuls stärker verändern.

\[ F=\frac{\Delta p}{\Delta t} \]

Beispiel

Ein Golfball (\(m = 20\;\text{g}\)) wird mit einem Kraftstoss (\(F = 67\;\text{N}\)) während 15 ms beschleunigt.

Welche Geschwindigkeit erreicht er?

---

Die Impulsänderung \(\Delta p\) erhalten wir aus der Definition der Kraft als zeitliche Änderung des Impulses:

\[ \Delta p = F \cdot \Delta t = 67\;\text{N} \cdot 0.015\;\text{s} \approx 1\;\frac{\text{kg}\;\text{m}}{\text{s}} \]

Die Impulsänderung entspricht der Differenz des Impuls vor (0) und nach dem Schlag (1).

\[ \Delta p = p_1 – p_0 \]

Da der Golfball vor dem Schlag keine Geschwindigkeit hatte, war sein Impuls \(p_0=0\). Somit ist der Impuls nach dem Schlag:

\[ p_1 = \Delta p = m \cdot v_1 \]

Wir lösen nach \(v_1\) auf und setzen \(\Delta p\) ein:

\[ v_1 = \frac{\Delta p}{\Delta t} = \frac{1\;\frac{\text{kg}\;\text{m}}{\text{s}}}{0.02\;\text{kg}} = 50\;\frac{\text{m}}{\text{s}} = 180\;\frac{\text{km}}{\text{h}} \]

Kraft durch Massenstrom (Rakete) 

Im obigen Beispiel haben wir gesehen, dass ein Kraftstoss auf einen Golfball eine Impulsänderung \(\Delta p\) zur Folge hat. Der Impuls ist definiert als Produkt von Masse und Geschwindigkeit:

 Für den Golfball haben wir gesagt, dass die Masse konstant bleibt und dass die Impulsänderung einer Änderung der Geschwindigkeit entspricht:

\[ \Delta p = \Delta (m \cdot v) = m \cdot \Delta v \]

In gleicher Art uns Weise können wir auch sagen, dass eine Impulsänderung \(\Delta p\) erreicht wird, wenn die Geschwindigkeit konstant bleibt, sich aber die Masse ändert:

\[ \Delta p = \Delta (m \cdot v) = \Delta m \cdot v \]

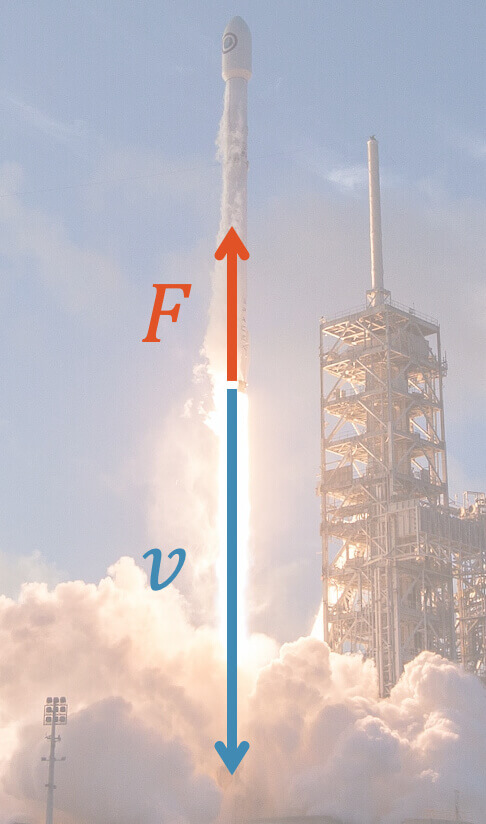
Das ist genau der Trick der Rakete! Sie stösst Masse mit hoher Geschwindigkeit ab und erreicht damit, dass sich ihr Impuls ändert bzw. eine Kraft auf sie wirkt:

\[ F = \frac{\Delta p}{\Delta t} = v \cdot \frac{\Delta m}{\Delta t} \]

Aus der obigen Gleichung erkennen wir, dass die Kraft \(F\) grösser wird, je mehr Masse pro Zeit (Massestrom) \(\frac{\Delta m}{\Delta t}\) ausgestossen wird und je grösser die Geschwindigkeit \(v\) ist. Wir haben also zwei Möglichkeiten, um eine Rakete zu optimieren: mehr Massestrom oder mehr Geschwindigkeit oder idealerweise beides gleichzeitig.

Kleine selbst gemachte Raketen aus einer PET-Flasche funktionieren mit Druckluft, die mit einer Velopumpe eingebracht wird. Sie fliegen aber viel höher, wenn wir zusätzlich Wasser einfüllen. Die Dichte von Wasser ist rund 1000 mal grösser als die Dichte von Luft, d.h. wir können mit Wasser viel mehr Masse in die PET-Flasche einbringen. Der aus der PET-Flasche austretende Wasserstrom erzeugt einen entsprechend grösseren Massestrom und wir haben damit eine viel grössere Kraft auf unsere Rakete.

Wenn wir aber zu viel Wasser in die PET-Flasche einfüllen, fliegt sie nicht mehr so hoch. Das Problem ist, dass die grosse Masse des Wassers auf eine grosse Höhe gebracht werden muss und das braucht wiederum viel potentielle Energie. Die echten Raketen optimieren die Kraft deshalb nicht über den Massestrom, sondern vor allem über die Austrittsgeschwindigkeit der Brennstoffgase an der Raketen-Düse.

Impulserhaltungssatz 

Der Impuls ist, wie die Ladung, die Masse, die Energie oder der Drehimpuls, eine Erhaltungsgrösse, d.h. er kann weder erzeugt, noch vernichtet werden. Er ist einfach da und kann einem System nur zu- oder abgeführt werden.

Besonders eindrücklich zeigt sich diese Tatsache bei Kollisionen – egal ob es sich um grosse Kollisionen von Fahrzeugen oder kleinste Zusammenstösse von Elementarteilchen wie z.B. Protonen oder Elektronen in Teilchenbeschleunigern handelt. Vor, während und nach der Kollision bleibt der Impuls erhalten!

Wir betrachten zwei Billardkugeln mit der gleichen Masse \(m\). Die rote Kugel (A) trifft mit einer Geschwindigkeit \(v\) auf die ruhende weisse Kugel (B).

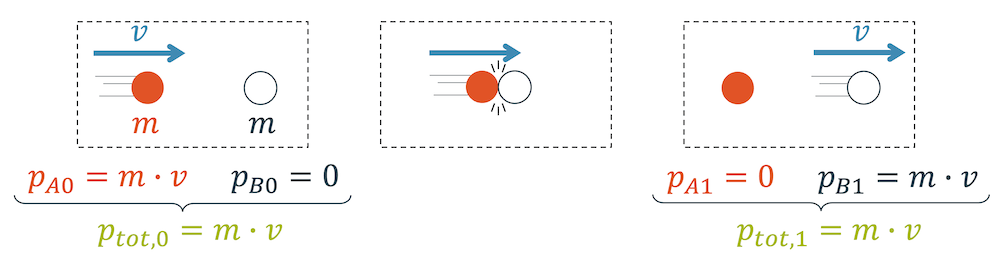
Vor der Kollision hat nur die rote Kugel einen Impuls (\(p_A = m v\)}. Die weisse Kugel hat keine Geschwindigkeit und deshalb keinen Impuls (\(p_B=0\)). Der Gesamtimpuls \(p_{tot,0}\) beider Kugeln vor der Kollision (0) ist deshalb:

\[ p_{tot,0} = mv + 0 = mv \]

Nach der Kollision (1) muss der Gesamtimpuls erhalten bleiben, d.h. wir verlangen unbedingt Impulserhaltung:

\[ p_{tot,1} = p_{tot,0} \]

Wir wissen aus Erfahrung, dass nach solch einer Kollision, die rote Kugel stoppt und die weisse Kugel weiter rollt. Da der Impuls beider Kugeln unbedingt gleich bleiben muss und jetzt der Gesamtimpuls nur von der weissen Kugel erbracht wird, ist ihr Impuls jetzt gleich gross, wie der Impuls der roten Kugel vor der Kollision. Da die weisse Kugel die gleiche Masse \(m\) hat, hat sie jetzt auch die gleiche Geschwindigkeit \(v\).

Beachten Sie, dass für eine einzelne Kugel keine Impulserhaltung gilt, da sie einem Kraftstoss ausgesetzt werden. Mit der Kollision ändert sich ihr Impuls. Die rote Kugel (A) gibt ihren ganzen Impuls ab. Sie hatte vor der Kollision (0) einen Impuls \(p_{A0} = mv\) und nach der Kollision (1) \(p_{A1}=0\). Daraus ergibt sich die negative Impulsänderung:

\[ \Delta p_A \quad = \quad p_{A1} – p_{A0} \quad = \quad 0 – mv \quad = \quad -mv \]

Für die weisse Kugel (B) haben wir durch die Kollision einen Gewinn an Impuls, d.h. eine positive Impulsänderung, denn sie hatte vorher (0) keinen Impuls \(p_{B0}=0\) und nachher (1) hatte sie den Impuls \(p_{B1}=mv\):

\[ \Delta p_B \quad = \quad p_{B1} – p_{B0} \quad = \quad mv – 0 \quad = \quad mv \]

Bei dieser Kollision ist der Impuls vom Betrag \(mv\) von der roten Kugel vollständig auf die weisse Kugel übertragen worden. Der Impuls hat intern die Hand gewechselt. Betrachten wir jedoch beide Kugeln zusammen als ein Gesamtsystem, so ist der Gesamtimpuls erhalten geblieben, sowohl in Betrag (\(mv\)), wie auch in Richtung (nach rechts).

Beispiel

Die weisse Kugel trifft gleichzeitig auf die Kugeln 2 und 8. Wir sehen, welche Geschwindigkeit die weisse Kugel und Kugel 2 nach der Kollision haben.

Welche Geschwindigkeit hat die schwarze Kugel 8 unter der Annahme, dass alle Kugeln die gleiche Masse \(m\) haben?

---

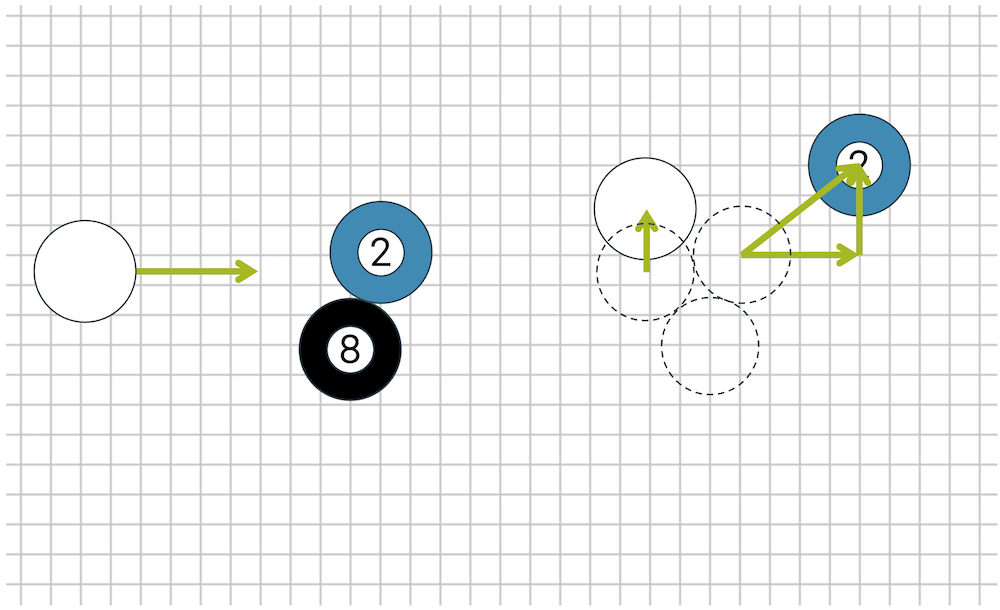
Um die Impulserhaltung anwenden zu können, brauchen wir zuerst den Gesamtimpuls vor der Kollision. Die beiden Kugeln 2 und 8 ruhen, d.h. sie tragen keinen Beitrag zum Gesamtimpuls bei. Die weisse Kugel hat vor der Kollision ein Geschwindigkeit von 6 Häuschen nach rechts. Der Gesamtimpuls beträgt somit “6” nach rechts.

Nach der Kollision muss der Gesamtimpuls immer noch gleich sein, d.h. auch “6” nach rechts. Betrachten wir vorerst nur die Richtung “nach rechts”, so sehen wir, dass die weisse Kugel nicht mehr zum Impuls beiträgt. Die Kugel 2 hat einen Beitrag von 4 Häuschen, d.h. “4”. Es fehlen noch “2” nach rechts und die müssen von der Kugel 8 erbracht werden.

Jetzt betrachten wir die die Richtung nach oben. Vor der Kollision war kein Impuls nach oben. Nach der Kollision bringt aber die weisse Kugel “2” und die Kugel 2 “3” nach oben. Wir haben also total “5” nach oben, die wir vorher nicht hatten! Die Kugel 8 muss deshalb “5” nach unten (bzw. “-5” nach oben) bringen, damit die Impulserhaltung auch in der Richtung nach oben erfüllt ist.

Zusammenfassend erhalten wir damit den notwendigen Impuls der Kugel 8: “2” nach rechts und “5” nach unten. Da die Kugel auch die Masse \(m\) hat, muss die Geschwindigkeit 2 Häuschen nach rechts und 5 Häuschen nach unten zeigen.

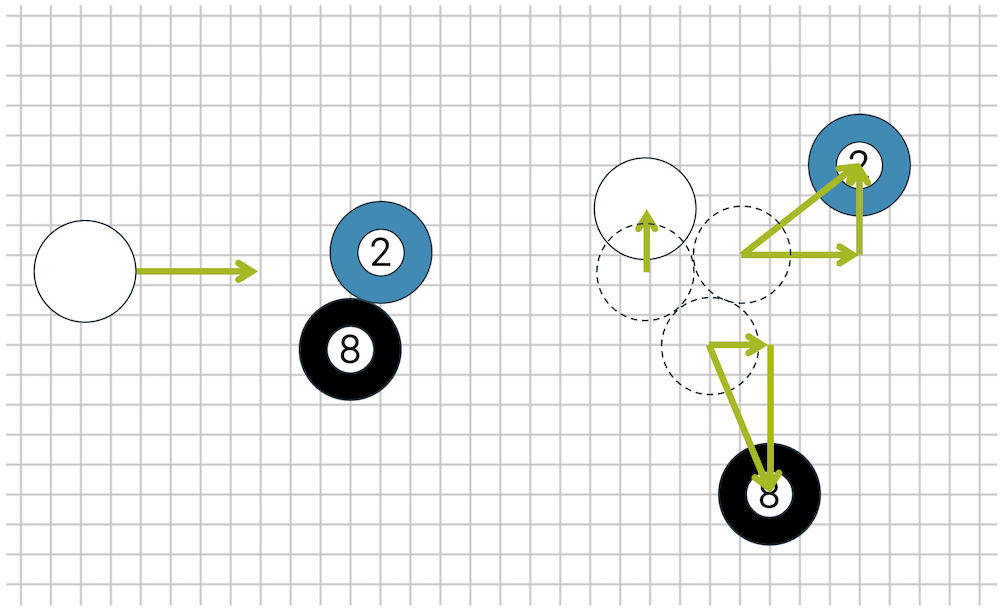
Das Gleiche sieht für den Impuls vor der Kollision in Vektorschreibweise folgendermassen aus:

\[ \require{cancel} \vec{p_{tot,0}} = \vec{p_{w,0}} + \cancel{\vec{p_{12,0}}} + \cancel{\vec{p_{8,0}}} = \begin{pmatrix} 6 \\ 0 \end{pmatrix} \]

Nach der Kollision haben wir den Impuls mit den beiden Unbekannten \(p_x\) und \(p_y\) für den Impuls der Kugel 8:

\[ \vec{p_{tot,1}} = \vec{p_{w,1}} + \vec{p_{12,1}} + \vec{p_{8,1}} = \begin{pmatrix} 0 \\ 2 \end{pmatrix} + \begin{pmatrix} 4 \\ 3 \end{pmatrix} + \begin{pmatrix} p_x \\ p_y \end{pmatrix} \]

Aus der Impulserhaltung \(\vec{p_{tot,0}}=\vec{p_{tot,1}}\) folgt die Vektorgleichung:

\[ \begin{pmatrix} 6 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \end{pmatrix} + \begin{pmatrix} 4 \\ 3 \end{pmatrix} + \begin{pmatrix} p_x \\ p_y \end{pmatrix} \]

Diese Vektorgleichung kann auch als zwei Gleichungen geschrieben werden:

\[ 6 = 0 + 4 + p_x \qquad \text{und} \qquad 0 = 2 + 3 + p_y \]

Daraus folgt der Impuls für Kugel 8:

\[ \vec{p_{8,1}} = \begin{pmatrix} p_x \\ p_y \end{pmatrix} = \underline{\begin{pmatrix} 2 \\ -5 \end{pmatrix}} \]

Impuls von Photonen 

Licht besteht aus Lichtteilchen, den sog. Photonen. Das sind masselose Energiepakete, die sich mit Lichtgeschwindigkeit \(c\) fortbewegen. Eigentlich sollten wir annehmen, dass Photonen keinen Impuls haben, da sie keine Masse haben. Es ist aber so, dass sie trotzdem Impuls haben. Der Impuls eines Photons ist absolut gesehen sicherlich sehr klein, aber er spielt für unsere Sonne eine extrem wichtige Rolle. Die Photonen, die im Zentrum der Sonne durch die Kernreaktion entstehen, wandern nach aussen und drängen mit ihrem Impuls das Gas zurück, das durch die Gravitation zum Zentrum “fallen” möchte. Man spricht hier vom Strahlungsdruck, der die Sonne vor der Implosion durch die eigene Schwerkraft hindert.

Das Gleichgewicht zwischen der Gravitationskraft, dem Gasdruck und eben dem Strahlungsdruck der Photonen herrscht in allen Sternen. Wenn die Fusionsreaktion im Innern des Sterns aufhört und der Strahlungsdruck nachlässt, kommt der Stern aus dem Gleichgewicht und implodiert zu einem weissen Zwerg, einem Neutronenstern oder einem schwarzen Loch.

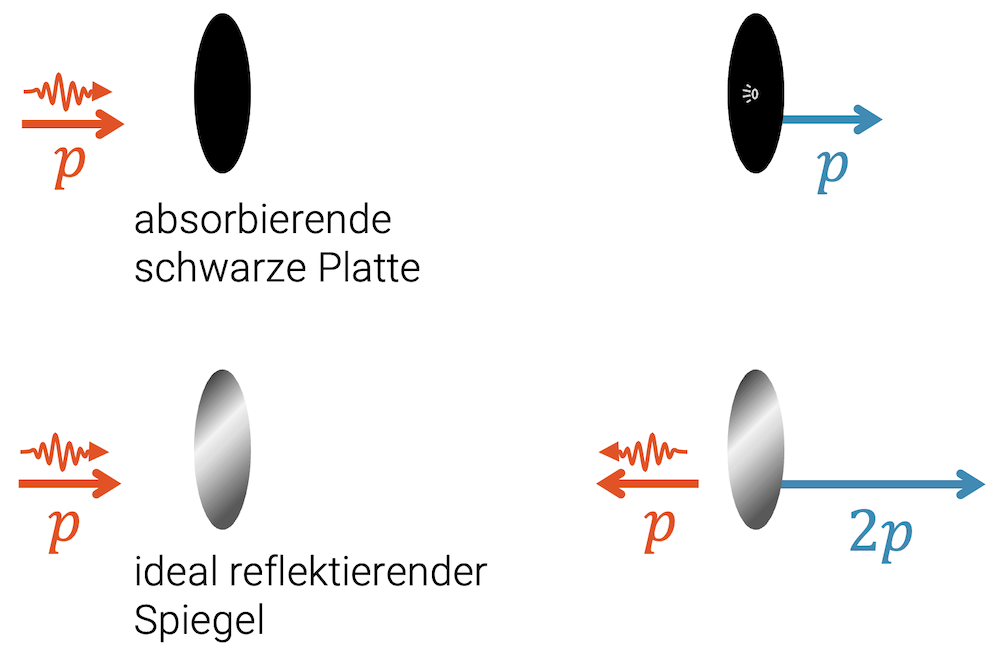
Fallen Photonen auf eine ideal schwarze Platte, so werden sie von der Platte absorbiert. Die Photonen geben ihre Energie an die Platte ab und erwärmen sie damit. Wie steht es mit dem Impuls? Der Impuls muss erhalten bleiben, d.h. der Impuls der Photonen wir an die Platte abgegeben, ähnlich wie im Beispiel mit den beiden Billardkugeln, wo der Impuls vollständig von der einen auf die andere Kugel übergeben wurde.

Bei einem Spiegel wird das Photon eigentlich auch absorbiert, aber es wird wieder in gleicher Art emittiert. Das neue Photon hat den gleichen Impuls \(p\), jedoch in die umgekehrte Richtung. Ist damit die Impulserhaltung gewährleistet? In Bezug auf den Betrag des Impulses schon, aber nicht in Bezug auf die Richtung. Wir hatten vorher den Impuls \(p\) nach rechts. Jetzt haben wir den Impuls \(p\) nach links oder eben \(-p\) nach rechts, d.h. wir haben \(2p\) weniger als vorher!

Der Spiegel übernimmt deshalb einen Impuls von \(2p\) nach rechts, so dass er in Summe mit dem Impuls des neuen Photons von \(-p\) wieder den Impuls des ursprünglichen Photons beibehält.

Elastischer Zwei-Körper-Stoss 

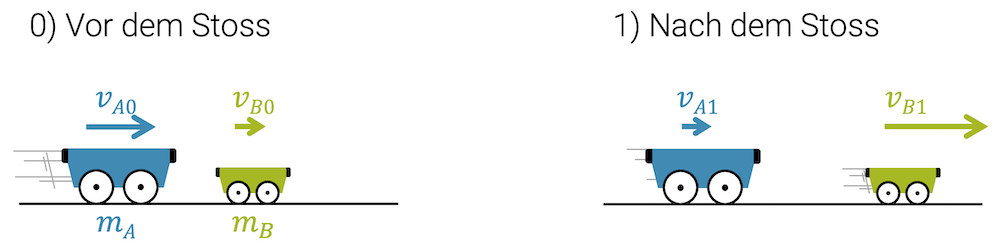
Wir wissen bereits, dass eine Kollision von zwei Körpern mit Hilfe der Erhaltung des Gesamtimpulses angeschaut werden kann. Der Gesamtimpuls vor der Kollision (0) ist die Vektorsumme der Körper A und B. In unserem Fall sind es zwei Wagen, aber wichtig ist hier nur, dass die beiden Körper eine Masse \(m_A\) bzw. \(m_B\) haben und eine Geschwindigkeit \(\vec{v}_{A0}\) bzw. \(\vec{v}_{B0}\):

\[ \vec{p}_{tot,0} = \vec{p}_{A0} + \vec{p}_{B0} = m_A \vec{v}_{A0} + m_B \vec{v}_{B0} \]

Wenn wir die Massen und die beiden Geschwindigkeiten \(\vec{v}_{A0}\) und \(\vec{v}_{B0}\) vor der Kollision haben, ist die Situation vollständig beschrieben. Wir können den Gesamtimpuls \(\vec{p}_{tot,0}\) berechnen.

Der Gesamtimpuls nach der Kollision (1) ist definiert als:

\[ \vec{p}_{tot,1} = \vec{p}_{A1} + \vec{p}_{B1} = m_A \vec{v}_{A1} + m_B \vec{v}_{B1} \]

Die Impulserhaltung liefert uns eine Gleichung:

\[ \vec{p}_{tot,0} = \vec{p}_{tot,1} \]

Da wir aber zwei Unbekannte haben, nämlich die beiden Geschwindigkeiten \(\vec{v}_{A1}\) und \(\vec{v}_{B1}\), können wir damit nicht eindeutig festlegen, wie schnell die beiden Wagen nach der Kollision sind. Das Experiment können wir aber beliebig wiederholen und die beiden Wagen “wählen” immer die gleiche Geschwindigkeit. Uns fehlt eine Gleichung.

Die Gesamtenergie der beiden Wagen vor (0) und nach (1) der Kollision bleibt ebenfalls erhalten. Wenn wir annehmen, dass die Kollision ohne Entwicklung von Wärme und ohne Veränderung der Wagen (keine Beule oder so) und die Schiene absolut horizontal ist, haben wir nur kinetische Energie im Spiel.

Das gibt uns eine zweite Gleichung. Aus \(E_{kin,0} = E_{kin,1}\) folgt:

\[ \frac{1}{2} m_A v_{A0}^2 + \frac{1}{2} m_B v_{B0}^2 \quad = \quad \frac{1}{2} m_A v_{A1}^2 + \frac{1}{2} m_B v_{B1}^2 \]

Mit Hilfe dieser zweiten Gleichung erhalten wir nach längerem Rechnen zwei Ausdrücke, mit welchen wir die Geschwindigkeiten der beiden Wagen nach der Kollision berechnen können. Beachten Sie hierbei, dass die Geschwindigkeit \(v_{A1}\) auch negativ sein kann. Das bedeutet nichts anderes, als dass die Richtung entgegen der anfänglichen Richtung von Wagen A \(\vec{v}_{A,0}\) gerichtet ist. Der Wagen A kann durch die Kollision wieder zurückgespickt werden.

Beispiel

Der Wagen A (Masse \(m_A = 2\;\text{kg}\)) trifft mit \(v_{A0}=3\;\frac{\text{m}}{\text{s}}\) auf den ruhenden Wagen B (Masse \(m_B = 0.1\;\text{kg}\)).

Welche Geschwindigkeiten haben die beiden Wagen nach der Kollision?

---

Wir wenden die beiden Gleichungen an und erhalten:

\[ v_{A1} = \frac{m_A – m_B}{m_A + m_B} \cdot v_{A0} + \frac{2m_B}{m_A + m_B} \cdot \cancel{v_{B0}} = \frac{(2-0.1)\;\text{kg}}{(2+0.1)\;\text{kg}} \cdot 3\;\frac{\text{m}}{\text{s}} = \quad 2.71\;\frac{\text{m}}{\text{s}} \]

\[ v_{B1} = \frac{m_B – m_A}{m_A + m_B} \cdot \cancel{v_{B0}} + \frac{2m_A}{m_A + m_B} \cdot v_{A0} = \frac{2\cdot2\;\text{kg}}{(2+0.1)\;\text{kg}} \cdot 3\;\frac{\text{m}}{\text{s}} = \quad 5.71\;\frac{\text{m}}{\text{s}} \]

Wenn wir alle Kombinationen von \(v_{A}\) und \(v_{B}\) als Punktschar in einem \(v_{A}\)-\)v_{B}\)-Diagramm aufzeichnen, so ergibt die Forderung nach \(p_{tot} = 6\;\frac{\text{kg m}}{\text{s}}\) eine Gerade, die von links oben nach rechts unten verläuft. Die Punktschar aller Kombinationen von \(v_{A}\) und \(v_{B}\) mit der Bedingung \(E_{kin}=9\;\text{J}\), gibt den Arm einer liegenden Parabel.

Es gibt genau zwei Punkte, die sowohl \(p_{tot} = 6\;\frac{\text{kg m}}{\text{s}}\) und \(E_{kin}=9\;\text{J}\) erfüllen. Es sind die Kombinationen: \(\;\;\) (2.71 m/s, 5.71 m/s) \(\;\;\) und \(\;\;\) (3 m/s, 0 m/s).

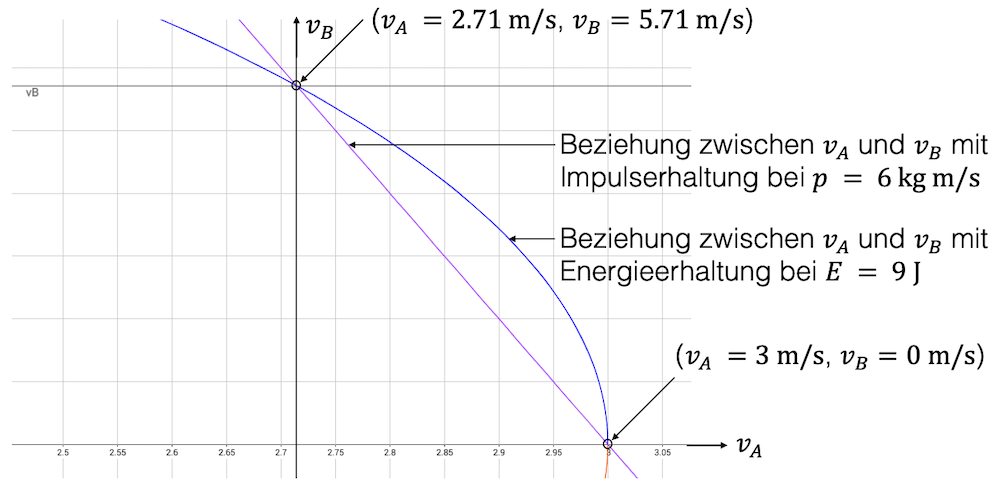
Bei einer elastischen Zwei-Körper-Kollision wechselt der eine Zustand in den anderen Zustand. Es gibt nur zwei zulässige Zustände und die sind exakt definiert.

Inelastischer Zwei-Körper-Stoss 

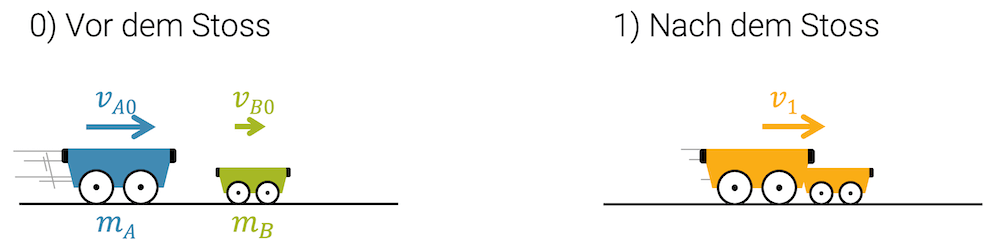
Beim vollkommen inelastischen Stoss “verschmelzen” die beiden Wagen zu “einer Masse”, die nach dem Stoss mit der Geschwindigkeit \(v_1\) unterwegs ist. Die Erhaltung der kinetischen Energie können wir nicht fordern, denn wir wissen ja, dass sie genau zwei Lösungen ergibt. Diese Lösungen haben wir beim elastischen Stoss behandelt. Beide haben unterschiedliche Geschwindigkeiten für A und für B. Es gibt keine Lösung, in welcher A und B die gleiche Geschwindigkeit haben.

Die Erhaltung des Impulses können wir weiterhin fordern. Der Gesamtimpuls vor der Kollision für beide Wagen muss gleich dem Gesamtimpuls für beide Wagen nach der Kollision sein.

\[ p_{tot,0} \quad = \quad m_A v_{A0} + m_B v_{B0} \quad = \quad (m_A + m_B) \cdot v_1 \quad = \quad p_{tot,1} \]

Wir lösen nach \(v_1\) auf und erhalten:

\[ v_1 = \frac{m_A v_{A0} + m_B v_{B0}}{m_A + m_B} \]

Die kinetische Energie bleibt nicht erhalten, aber die Gesamtenergie schon. Der Verlust an einem Teil der kinetischen Energie nach der Kollision kann durch eine Umwandlung in Wärme erklärt werden.

Beachte, dass reale Kollisionen immer eine Mischung von elastischem und inelastischem Stoss sind. Es muss nicht gerade soweit gehen, dass beide Körper miteinander “verschmelzen”, sondern sie können durchaus nach der Kollision noch eine eigene Geschwindigkeit haben. Ein Teil der kinetischen Energie wird aber in Wärme umgewandelt.

Simulation 

Mit der folgenden Simulation kannst du elastische und inelastische Stösse simulieren und auch ihre Berechnungen überprüfen – setze für die Anzeige der Daten die entsprechenden Häkchen.

• Simulation von Kollisionen