Das Wichtigste in Kürze
Die allgemeine Form der Gleichung einer Kugel \(K\) in Koordinatenform lautet:
\[ K \colon \;\; (x-Z_x)^2 + (y-Z_y)^2 + (z-Z_z)^2 = r^2 \]
Die Kugel ist eine Punktschar aller Punkte \(Q(x,y,z)\), die zum Zentrum \(Z(Z_x,Z_y,Z_z)\) alle den gleichen Abstand, nämlich den Radius \(r\) haben. Sie ist eine flächige Punktschar wie eine Ebene, jedoch als Kugel gekrümmt.
Videos
-
Schnittpunkte Gerade und Kugel (5051-4)
-
Tangente an eine Kugel (5051-5)
-
Schnittkreis einer Ebene mit einer Kugel (5051-6)
-
Gleichung einer Kugel (Teil 1) (Tutorial)
Dauer: 8 min 34 s
-
Gleichung einer Kugel (Teil 2) (Tutorial)
Dauer: 13 min 38 s
Die Punkte auf der Kugeloberfläche haben eines gemeinsam: Sie haben alle den gleichen Abstand zum Kugelzentrum \(Z\) und dieser Abstand heisst Radius der Kugel \(r\). Die Kugel ist in drei Dimensionen das, was der Kreis in zwei Dimensionen ist. Wir können deshalb unsere Überlegungen vom Kreis jetzt auf drei Dimensionen übertragen.
Die nachstehende Grafik zeigt eine Kugel mit Radius \(r=2\). Die Punkte \(P_1(2,0,0)\), \(P_2(0,2,0)\) und \(P_3(0,0,2)\) haben alle den Abstand \(r=2\) zum Zentrum im Ursprung \(Z(0,0,0)\). Wenn wir irgendeinen Punkt \(Q(Q_x,Q_y,Q_z)\) auf der Kugeloberfläche betrachten, dann hat auch dieser Punkt einen Abstand \(r=2\) zum Zentrum.
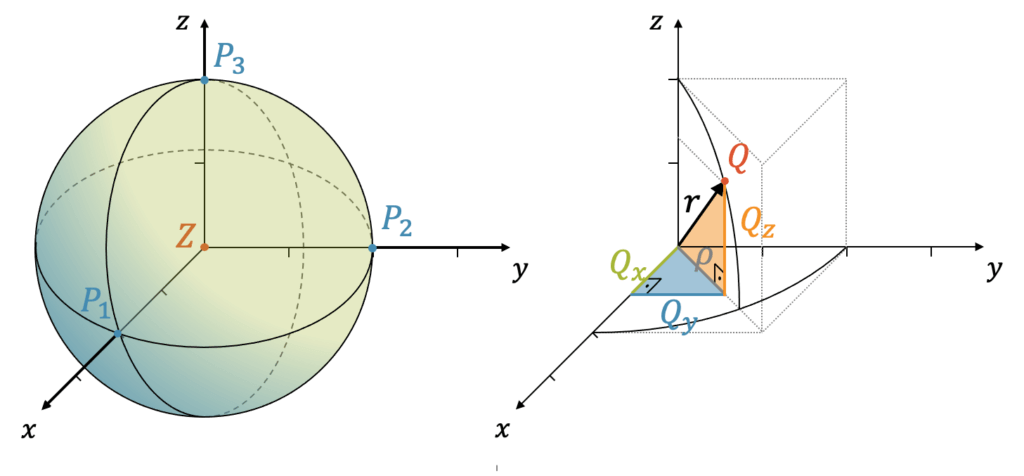
Zuerst benutzen wir den Satz des Pythagoras und berechnen die graue Hypotenuse \(\rho\) des liegenden rechtwinkligen Dreiecks (blau eingefärbt):
\[ \rho = \sqrt{(Q_x)^2+(Q_y)^2} \]
Jetzt können wir das stehende rechtwinklige Dreieck (orange eingefärbt) berechnen:
\[ r = \sqrt{\rho^2+(Q_z)^2} \]
Wenn wir den Ausdruck für \(\rho\) von oben einsetzen, erhalten wir:
\[ r = \sqrt{\Big( (Q_x)^2+(Q_y)^2 \Big)+(Q_z)^2} \]
Ohne Klammern und quadriert haben wir damit:
\[ r^2 = (Q_x)^2 + (Q_y)^2 + (Q_z)^2 \]
Für irgendeinen Punkt \(Q\) auf der Kugel gilt im allgemeinen Fall wieder:
\[ \overrightarrow{ZQ} = \overrightarrow{OQ} – \overrightarrow{OZ} \]
Die linke Seite hat den Vektor \(\overrightarrow{ZQ}\), der die Rolle des Radius übernimmt. Sein Betrag bzw. seine Länge entspricht natürlich \(r\). Die rechte Seite ist gleich diesem Vektor und somit ist die Länge der Vektordifferenz auf der rechten Seite auch gleich \(r\).
\[ r = \Big|\overrightarrow{ZQ}\Big| = \Big|\overrightarrow{OQ} – \overrightarrow{OZ}\Big| \]
\[ r = \sqrt{(ZQ_x)^2 + (ZQ_y)^2 + (ZQ_z)^2} \]
\[ = \sqrt{(x-Z_x)^2 + (y-Z_y)^2 + (z-Z_z)^2} \]
Wir quadrieren und erhalten die Gleichung der Kugel. Sie ist eigentlich genau wie die Kreisgleichung, jedoch mit einer Dimension mehr:
\[ (x-Z_x)^2 + (y-Z_y)^2 + (z-Z_z)^2 = r^2 \]
Für die oben abgebildete Kugel haben wir \(Z(Z_x,Z_y,Z_z)\), d.h. \(Z_x=0\), \(Z_y=0\) und \(Z_z=0\) und \(r=2\). In die Gleichung eingesetzt, erhalten wir:
\[ x^2 + y^2 + z^2 = 4 \]
Beispiel: Kugel berührt Ebene
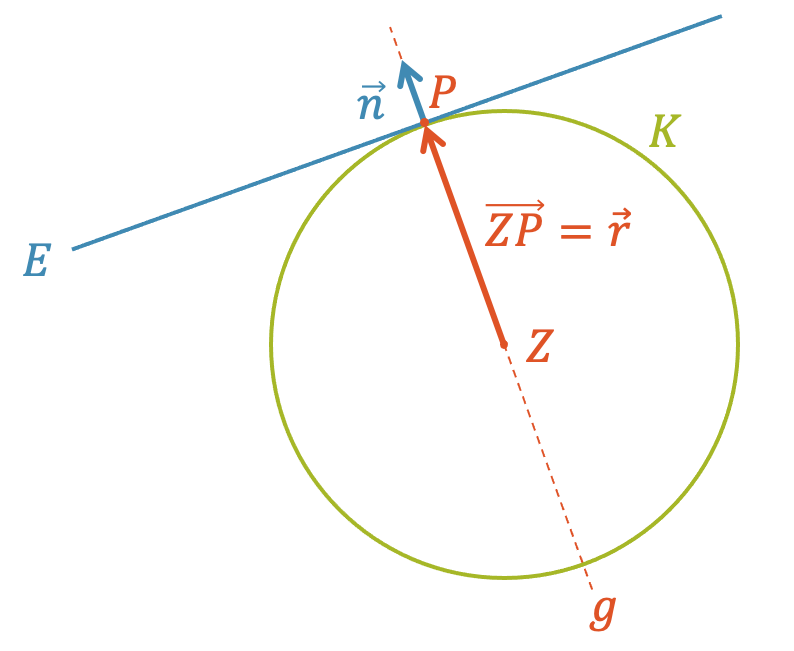
Finde die Gleichung der Kugel \(K\), die das Zentrum in \(Z(-4,1,1)\) hat und die die Ebene \(E\) gerade berührt.
\[ E \colon \;\; 4x – 2y – z = 2 \]
Wir machen eine kleine Skizze:
Wir erkennen, dass wir den Lotfusspunkt \(P\) brauchen, der durch das Lot von \(Z\) auf \(E\) entsteht. Aus der Ebenengleichung lesen wir den Normalvektor ab:
\[ \vec{n} = \begin{pmatrix} 4 \\ -2 \\ -1 \end{pmatrix} \]
Mit \(Z\) als Stützpunkt und \(\vec{n}\) als Richtungsvektor haben wir die Gleichung der Geraden \(g\), die das Lot beschreibt:
\[ g \colon \;\; \begin{pmatrix} -4 \\ 1 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} 4 \\ -2 \\ -1 \end{pmatrix} \]
Jetzt setzen wir die Ausdrücke für die Koordinaten der Punkte auf der Geraden in die Ebenengleichung ein, d.h. wir suchen den bestimmten Wert des Parameters \(s\), so dass die Gerade auch die Ebene erfüllt. Damit haben wir den Lotfusspunkt.
\[ \begin{array}{cc} x = -4 + 4s \\ y = 1 – 2s \\ z = 1 – s \end{array} \]
\[ 4 \cdot (-4 + 4s) – 2 \cdot (1 – 2s) – (1 – s) = 2 \]
\[ \rightarrow \quad s=1 \]
\[ \overrightarrow{OP} = \begin{pmatrix} -4 \\ 1 \\ 1 \end{pmatrix} + 1 \cdot \begin{pmatrix} 4 \\ -2 \\ -1 \end{pmatrix} = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} \]
Jetzt haben wir den Lotfusspunkt \(P(0,-1,0)\). Die Länge des Verbindungsvektors \(\overrightarrow{ZP}\) ist unser Radius, den wir für die Kugelgleichung brauchen:
\[ \overrightarrow{ZP} = \begin{pmatrix} 0-(-4) \\ -1-1 \\ 0-1 \end{pmatrix} = \begin{pmatrix} 4 \\ -2 \\ -1 \end{pmatrix} \]
\[ \big| \overrightarrow{ZP} \big|^2 = r^2 = 4^2 + (-2)^2 + (-1)^2 = 21 \]
Jetzt können wir die Kugelgleichung aufstellen:
\[ \underline{(x+4)^2 + (y-1)^2 + (z-1)^2 = 21} \]
Eine andere Methode ist die Berechnung des Abstandes \(d = r\) des Punktes \(Z\) von der Ebene \(E\). Wir brauchen dazu irgendeinen Punkt \(A\) auf der Ebene. Dazu setzen wir z.B. \(x=0\), \(y=0\) und berechnen die \(z\)-Koordinate mit Hilfe der Ebenengleichung:
\[ z = 4x – 2y – 2 = -2 \]
\[ \rightarrow \quad A(0,0,-2) \in E \]
Jetzt benutzen wir die Formel für die Berechnung des Abstands:
\[ d = \frac{\Big|\vec{n} \cdot \Big(\overrightarrow{OZ}-\overrightarrow{OA}\Big)\Big|}{\big| \vec{n} \big|} \]
\[ = \frac{\Big|\begin{pmatrix} 4 \\ -2 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} -4-0 \\ 1-0 \\ 1-(-2) \end{pmatrix}\Big|}{\sqrt{4^2+(-2)^2+(-1)^2}} \]
\[ = \frac{\Big| 4 \cdot (-4) + (-2) \cdot 1 + (-1) \cdot 3 \Big|}{\sqrt{16+4+1}} \]
\[ = \frac{|-21|}{\sqrt{21}} = \sqrt{21} \]
Damit ist \(r=d=\sqrt{21}\) bzw. \(r^2=21\). Mit den Koordinaten von \(Z\) und mit \(r^2\) können wir die Kugelgleichung wieder aufstellen.
Aufgabensammlung
-
Kreise und Kugeln (5051) – Aufg. 4
1 Aufgabe (pdf/Video-Lösung):
Schnittpunkte Gerade und Kugel -
Kreise und Kugeln (5051) – Aufg. 5
3 Teilaufgaben (pdf/Video-Lösung):
Tangente an eine Kugel -
Kreise und Kugeln (5051) – Aufg. 6
1 Aufgabe (pdf/Video-Lösung):
Schnittkreis einer Ebene mit einer Kugel
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
Weitere Links
Kugel (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.