Inhalt
Das Wichtigste in Kürze
Die Beschleunigung ist die Änderung der Geschwindigkeit \(\Delta v\) pro Zeit \(\Delta t\):
\[a=\frac{\Delta v}{\Delta t}\]
Die Beschleunigung hat deshalb die Einheit: \(\;[\,a\,] = \large\frac{\text{m}}{\text{s}^2}\)
-
- positive Beschleunigung \((a>0)\): Die Geschwindigkeit nimmt zu: \(\Delta v > 0\)
- keine Beschleunigung \((a=0)\): Die Geschwindigkeit bleibt konstant: \(\Delta v = 0\)
- negative Beschleunigung \((a<0)\): Die Geschwindigkeit nimmt ab: \(\Delta v < 0\)
Die Beschleunigung ist eine Vektorgrösse, d.h. \(a = |\vec{a}|\) ist der Betrag des Beschleunigungsvektors \(\vec{a}\), der auch eine Richtung hat: Der Beschleunigungsvektor zeigt in die Richtung, in welche die Geschwindigkeit zunehmen soll. Falls die Beschleunigung entgegen der aktuellen Geschwindigkeit gerichtet ist, heisst das, dass diese Geschwindigkeit abgebaut wird (Bremsvorgang).
Weitere Artikel zu diesem Thema:
Tutorial Videos
(Es gibt leider keine Tutorial Videos zu diesem Thema)
Beschleunigung und Geschwindigkeit
Stell dir vor, du hast einen Kleinwagen gekauft. Kannst du mit diesem Auto auf der Autobahn mit 120 km/h fahren? Ja, klar. Der Motor ist zwar klein, aber auch Kleinwagen können diese Geschwindigkeit erreichen. Sie brauchen nur etwas mehr Zeit dafür. 😎

Ein Kollege schwärmt von seiner neuesten Anschaffung, einem Sportwagen. Natürlich kann auch er mit 120 km/h auf der Autobahn fahren. Die beiden Autos, so unterschiedlich sie auch sind, fahren in so einem Fall gleich schnell. 🤔

Der Sportwagen kann aber die Geschwindigkeit von 120 km/h (wie auch jede andere Geschwindigkeit) in viel kürzerer Zeit erreichen.
Der Unterschied zwischen den beiden Wagen ist die Beschleunigung, d.h. die Änderung der Geschwindigkeit in einer bestimmten Zeit. Der Kleinwagen kann von 0 auf 100 km/h beschleunigen, braucht dafür aber 15-20 Sekunden. Ein Sportwagen wird dies in ein paar wenigen Sekunden schaffen.
Interpretation der Beschleunigung
Um das Gefühl für die Grösse Beschleunigung zu verbessern, betrachten wir Motorräder, deren Vorder- oder Hinterrad uns verraten, ob sie ab Beschleunigen oder am Abbremsen sind.
Wir unterscheiden bei der Beschleunigung die folgenden Fälle:
- positive Beschleunigung \((a>0)\): Die Geschwindigkeit nimmt zu: \(\Delta v > 0\)
- keine Beschleunigung \((a=0)\): Die Geschwindigkeit bleibt konstant: \(\Delta v = 0\)
- negative Beschleunigung \((a<0)\): Die Geschwindigkeit nimmt ab: \(\Delta v < 0\)
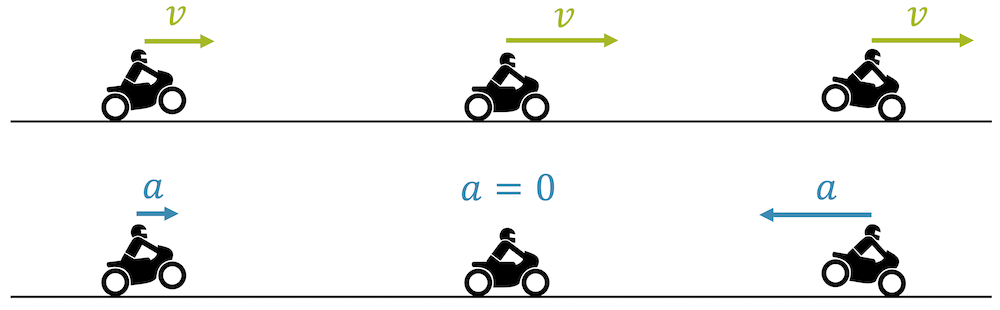
Eine positive Beschleunigung \(a>0\) bedeutet, dass die Geschwindigkeit mit der Zeit im Betrag zunimmt. Die Geschwindigkeitsänderung /(\Delta v\) ist positiv. In den üblichen Fällen spricht man von “Beschleunigen”. Bei einem Motorrad kann eine grosse Beschleunigung beobachtet werden, indem das Vorderrad des Motorrads angehoben wird.

Wenn wir die Richtungen der Geschwindigkeit und der Beschleunigung anschauen, die ja beides Vektorgrössen sind, so zeigt bei positiver Beschleunigung der Vektor der Beschleunigung in die gleiche Richtung, wie die Geschwindigkeit und baut diese aus.
Wie müssen wir uns eine Bewegung ohne Beschleunigung vorstellen? Keine Beschleunigung heisst nicht etwa, dass das Objekt sich nicht mehr bewegt, sondern viel eher, dass die Geschwindigkeit keine Änderung erfährt, also konstant bleibt. Da die Beschleunigung die Veränderung der Geschwindigkeit darstellt, folgt aus \(\Delta v = 0\) direkt \(a=0\), was auch \(v\)= konstant bedeutet.

Beachte, dass Körper und Systeme, die in Ruhe sind (z.B. Gebäude, Brücken, ruhende Gegenstände etc.) eine Geschwindigkeit von \(v=0\) haben. Weil sich diese Geschwindigkeit nicht ändert, gilt auch \(a=0\). Der Körper oder das System ist in Ruhe und bleibt in Ruhe.
Wenn die Beschleunigung negativ ist, ist die Veränderung eine Abnahme der Geschwindigkeit: \(\Delta v < 0 \).
Umgangssprachlich nennen wir das ein Abbremsen. Physikalisch gesehen ist es einfach eine negative Beschleunigung oder eine Beschleunigung, deren Vektor dem Geschwindkeitsvektor entgegen gesetzt ist. Bei einem Motorrad, sehen wir bei starker negativer Beschleunigung ein deutliches Herunterdrücken des Vorderrads und manchmal auch ein Anheben des Hinterrads.

Beispiel
Gleichmässig beschleunigte Bewegung
Die gleichmässig beschleunigte Bewegung ist ein Spezialfall, in welchem die Beschleunigung konstant ist. Wenn wir eine konstante positive Beschleunigung nehmen und im a-t-Diagramm aufzeichnen, erhalten wir den Verlauf wie folgt:
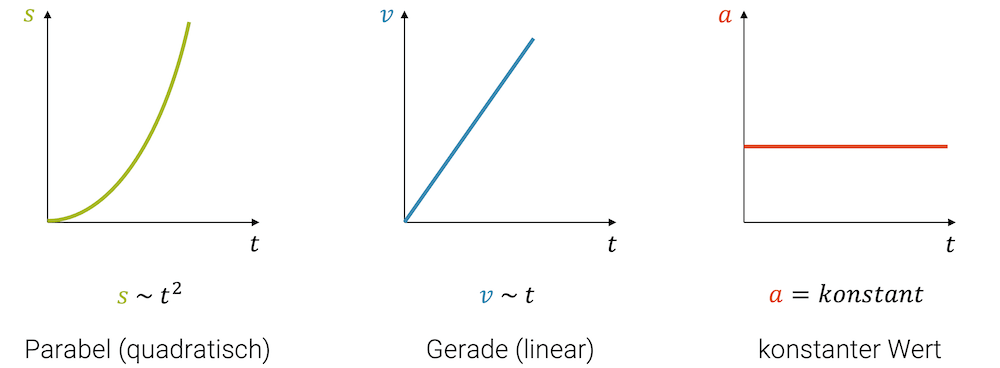
Bei einer konstanten (positiven) Beschleunigung nimmt die Geschwindigkeit mit einer konstanten Rate pro Zeit zu: Die Geschwindigkeit hat eine positive konstante Steigung im v-t-Diagramm. Das v-t-Diagramm zeigt deshalb einen linearen (steigenden) Verlauf. Weil die Steigung im v-t-Diagramm konstant ist, können wir für die Beschleunigung einen konstant positiven Wert nehmen.
Beachte, dass die halbe Parabel (quadratische Funktion) im s-t-Diagramm zu einer linearen Funktion im v-t-Diagramm und schliesslich zu einer Konstanten im a-t-Diagramm führt. Mathematisch ist das jeweils die Ableitungsfunktion der vorigen Funktion:
\[ s(t) = k \cdot t^2 \]
\[ v(t) = \frac{d}{dt}s(t) = 2k \cdot t \]
\[ a(t) = \frac{d}{dt}v(t) = \frac{d^2}{dt^2}s(t) = 2k \]
Weitere Videos
(keine externe Youtube-Videos zu diesem Thema)
Aufgabensammlung
Lernziele
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt














Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.