Phasenübergänge

Was ist eine Phase?

Als Phase wird ein Gebiet bezeichnet, das homogen in Zusammensetzung und Aggregatzustand ist. Beispielsweise bildet flüssiges Wasser eine Phase. Eine Blase Wasserdampf im kochenden Wasser wäre eine zweite (gasförmige) Phase.

Jeder Aggregatzustand eines Stoffes bildet eine Phase. Manchmal kommen zwei Aggregatzustände gleichzeitig vor. Wir sprechen dann von zwei Phasen oder davon, dass wir im Zweiphasengebiet sind.

Bei Gemischen können zwei Stoffe eine oder zwei Phasen bilden.

Das Wasser enthält im Normalfall gelöste Mineralien, ist demnach ein Gemisch. Luft ist selber auch ein Gasgemisch. Weil beides homogene Gemische sind, erscheinen sie uns wie ein reiner Stoff und bilden deshalb nur eine Phase. Zu den homogenen Gemischen, die nur eine Phase bilden, gehören:

• Gasgemische
• Flüssige Lösungen (Gelöster Feststoff oder gelöste Flüssigkeit)
• Legierungen

Bei heterogenen Gemischen, bilden die beiden Komponenten zusammen zwei Phasen:

• Suspension (nicht gelöster Feststoff in Flüssigkeit)
• Emulsion (nicht gelöste Flüssigkeitstropfen in anderer Flüssigkeit)
• Aerosol (Flüssigkeits- oder Feststoffpartikel in Gas)
• Schaum (Gasblasen in Flüssigkeit)

Phasenübergänge zwischen den Aggregatzuständen

Wenn wir uns auf einen Reinstoff beschränken, gibt es die Übergänge von einem Aggregatzustand zum nächsten. Es gibt drei Phasenübergänge plus jeweils deren drei Umkehrungen:

• Verdampfen (Sieden, Verdunsten) und dessen Umkehrung, das Kondensieren
• Schmelzen und dessen Umkehrung, das Erstarren oder Kristallisieren
• Sublimation, der direkte Übergang von einem Feststoff zum Gas und die Resublimation, wenn ein Gas Kristalle formt

Die folgende Grafik zeigt die 6 Phasenübergänge im Teilchenmodell:

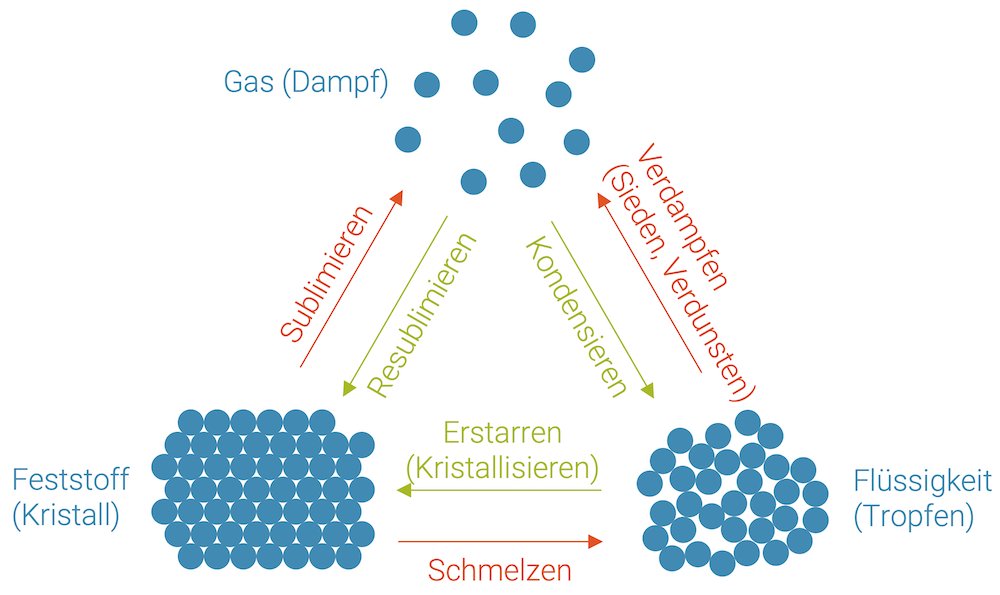
Spezifische Schmelz- und Verdampfungswärme

Für einen Phasenübergang braucht jedes Teilchen eine bestimmte Menge an Energie, wenn eine Bindung überwunden werden soll. Analog wird Energie frei, wenn eine Bindung eingegangen wird, da dies einem tieferen Energieniveau entspricht, d.h. das Teilchen gibt Energie ab.

Die spezifische Menge an Energie (pro Kilogramm), die für das Schmelzen benötigt wird, ist die spezifische Schmelzwärme \(L_f\) des betreffenden Stoffs.

Die Energie, die für das Verdampfen eines Kilogramms benötigt wird, heisst spezifische Verdampfungswärme \(L_v\).

Wenn einem Stoff am Phasenübergang Wärme zugeführt wird, so bleibt die Temperatur konstant. Die Energie führt nicht zu stärkeren Teilchenbewegungen, sondern wird für die Überwindung der Bindungen gebraucht.

Mit dem Modell des Energiepotenzialtopfs im Kopf, verstehen wir, dass eine Zufuhr von Energie an einen kleinen Kristall die nötige Energie liefert, um die Teilchen aus dem energetisch tiefsten Topf zu befreien und auf ein höheres Energieniveau zu heben.

Diese Energie wird nicht pro Teilchen, sondern pro Kilogramm des betreffenden Stoffs angegeben. Sie heisst spezifische Schmelzwärme \(L_f\).

Wenn wir diese gleiche Energiemenge von einem gleich grossen Flüssigkeitstropfen abführen, so erstarrt dieser Tropfen zu einem Kristall. Ein erstarrender Tropfen gibt die sog. Kristallisationswärme ab, die gleich gross ist, wie die Energiemenge, die es braucht, um den Kristall wieder zu einem Tropfen zu schmelzen.

In der Flüssigkeit bewegen sich die Teilchen, gegenüber dem Feststoff, auf einem höheren Energieniveau, das die Bewegung innerhalb des Tropfens zulässt. Die Teilchen können den Tropfen jedoch nicht verlassen.

Die Tropfengrenze hat gewissermassen einen energetisch hohen ”Topfrand”. Der ganze Tropfen ist jetzt ein Potenzialtopf und die Teilchen haben zu wenig Energie, um aus ihm auszubrechen.

Das Befreien der einzelnen Teilchen aus dem Verbund des Tropfens, entspricht dem Anheben der Teilchen über den energetischen ”Rand” des grossen Potenzialtopfs des Tropfens hinaus. Die Energie, die dazu pro Kilogramm nötig ist, heisst spezifische Verdampfungswärme \(L_v\).