
Dämpfer haben eine wichtige Aufgabe in der Mechanik, v.a. bei Schwingungen. Ein Dämpfer beim Fahrrad erhöht den Komfort und verteilt einen Kraftstoss über eine längere Zeitperiode, so dass die auftretenden Kräfte kleiner werden. Das hat eigentlich nicht direkt mit Schwingungen zu tun. Wenn wir aber solche Dämpfer bei schwingenden Systemen einsetzen, haben sie eine typische Wirkung: Sie entnehmen Energie aus dem schwingenden System und dämpfen die Schwingung ab.
Beim ungedämpften System bleibt die totale Energie im System \(E_{tot}\) konstant und damit bleibt auch die Amplitude konstant.
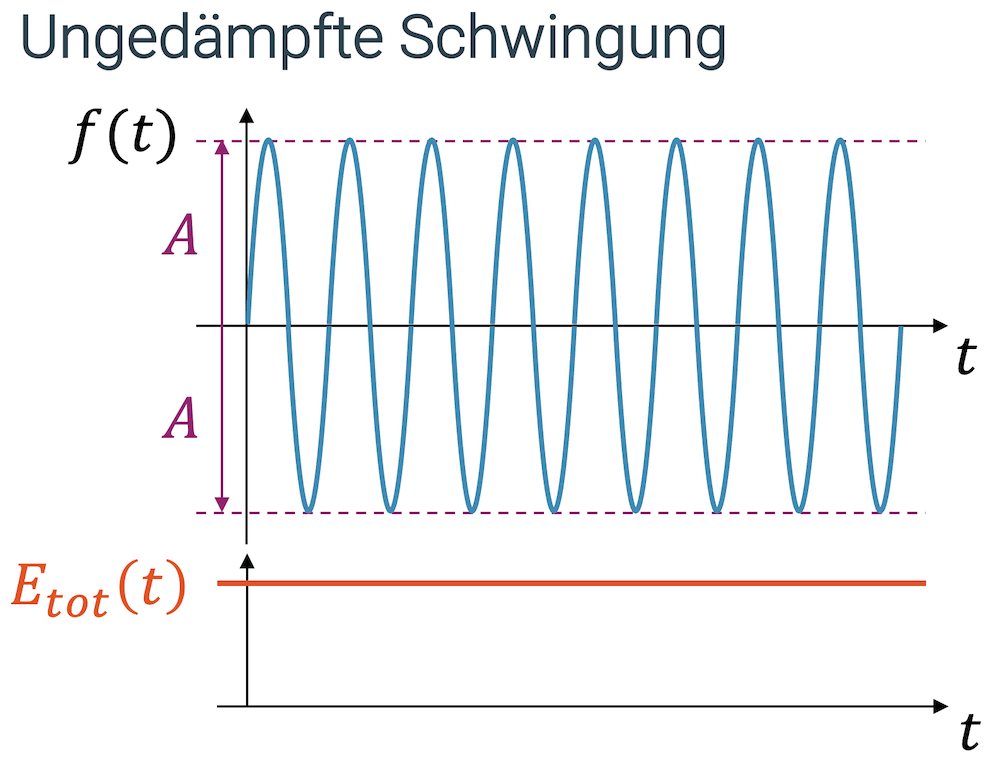
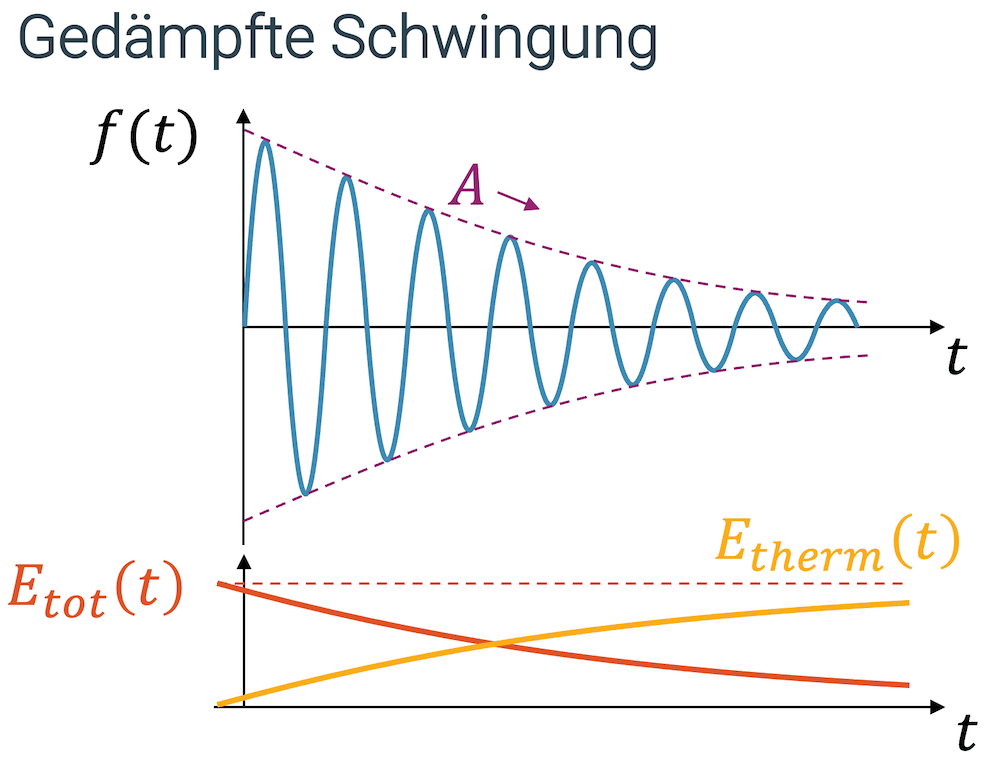
Da im gedämpften System die Energie im schwingenden System abnimmt, klingt die Schwingung ab und die Amplitude wird kleiner, bis die Schwingung komplett verschwindet. Der Teil der Energie, der in Wärme umgewandelt worden ist, steht für die Schwingung nicht mehr zur Verfügung.
Dämpfer entnehmen dem schwingenden System einen Teil der Energie und wandeln diesen in Wärme (thermische Energie) um. Als Folge klingt die Amplitude der Schwingung ab.
Funktionsweise eines Dämpfers
In der nachfolgenden Skizze ist ein Federpendel, zusätzlich mit einem Dämpfer ausgestattet. Der Dämpfer besteht einfach aus einer Platte, die sich in der Flüssigkeit hoch- und runterbewegt. Bei der Abwärtsbewegung (Bild links) wird die Flüssigkeit unter der Platte nach oben verdrängt. Da zwischen Platte und Gefässwand nur eine enge Öffnung gegeben ist, entsteht hier eine Widerstandskraft \(F_W\), die der Plattenbewegung \(\dot{x}\) entgegen gerichtet ist, d.h. nach oben.
Die Notation \(\dot{x}\) beschreibt die erste Ableitung der Position \(x\) nach der Zeit \(t\), was natürlich der Geschwindigkeit \(v(t)\) entspricht:
\[ \dot{x}(t) = \frac{d}{dt} x(t) = v(t) \]
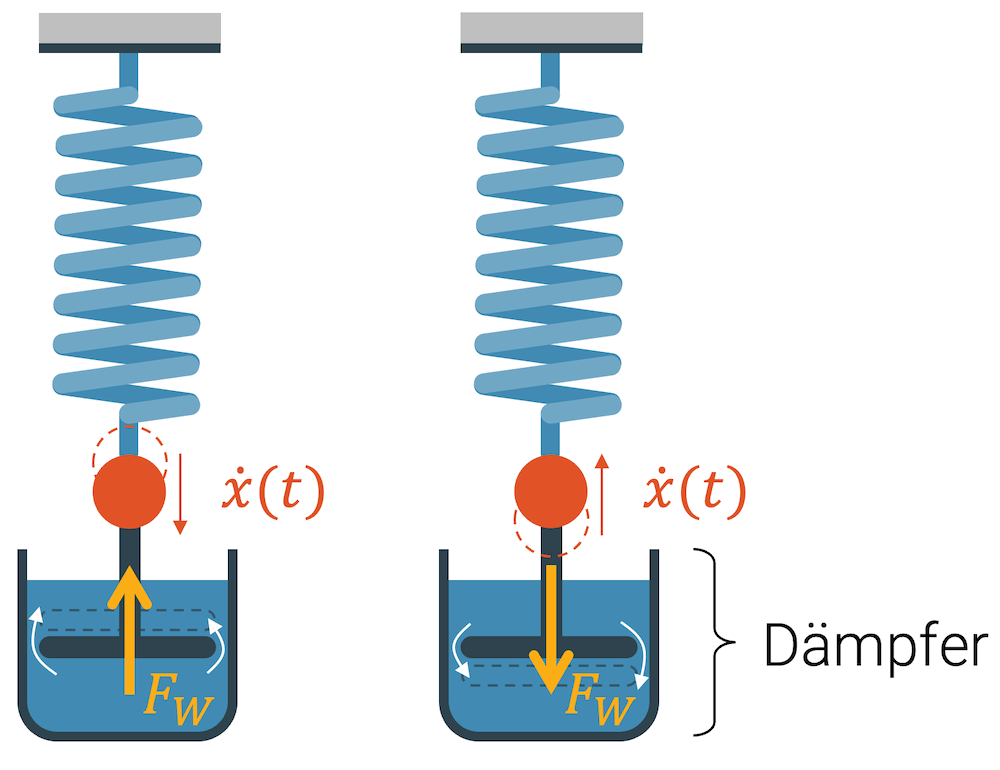
Bei der Rückwärtsbewegung (nach oben, Bild rechts) fliesst die Flüssigkeit wieder nach unten, in der engen Stelle, an der Platte vorbei. Die Platte wird deshalb mit einer Kraft nach unten dieser Aufwärtsbewegung entgegen wirken. Das ist ein bisschen wie der Stiefel, der in tiefen Schlamm versunken ist und nur noch mit viel Kraft herausgezogen werden kann.
Oft liegt die Platte bei Dämpfern an der Zylinderwand an und die Flüssigkeit wird durch kleine Löcher in der Platte geleitet. Als Flüssigkeit eignen sich Öle, die zusätzlich noch etwas viskoser sind, d.h. noch etwas mehr Kraft brauchen, um durch die kleinen Löcher zu fliessen.
Ein Dämpfer bewegt eine Platte in einer eingeschlossene Flüssigkeit und zwingt diese durch eine schmale Öffnung oder Löcher durchzufliessen. Durch die innere Reibung in der Flüssigkeit entsteht eine Widerstandskraft, die proportional zur Geschwindigkeit der Platte ist.
Durch die Verwirbelungen und die innere Reibung in der Flüssigkeit wird mechanische Arbeit in Wärme umgewandelt.
Differentialgleichung der gedämpften Schwingung
Für das ungedämpfte Federpendel haben wir die folgende Differentialgleichung:
\[ m \cdot \ddot{x}(t) + k \cdot x(t) = 0 \]
Wie diese Differentialgleichung zustande kommt, kann im Artikel zur harmonischen Schwingung nachgelesen werden. Der Term \(k \cdot x(t)\) steht für die Rückstellkraft der Feder. Sie ist der Position \(x(t)\) entgegen gerichtet.
Wenn wir einen Dämpfer haben, dann ist seine Kraft der Richtung der Geschwindigkeit \(\dot{x}(t)\) entgegen gerichtet und proportional zu ihr: Je grösser die Geschwindigkeit, desto grösser die Dämpfungskraft. Wir setzen die Dämpfungskraft deshalb analog zur Rückstellkraft mit positivem Vorzeichen in die Differentialgleichung ein und erhalten:
\[ m \cdot \ddot{x}(t) + b \cdot \dot{x}(t) + k \cdot x(t) = 0 \]
Dabei ist \(b\) die sog. Dämpfungskonstante, die bestimmt, wie stark die Dämpfungskraft für eine bestimmte Geschwindigkeit \(\dot{x}(t)\) sein soll.
Um diese Differentialgleichung zu lösen, nehmen wir den folgenden Ansatz mit einem unbekannten Parameter \(\lambda\):
\[ x(t) = e^{\lambda t} \]
Wir leiten zwei mal ab und kriegen:
\[ \dot{x}(t) = \lambda \cdot e^{\lambda t} \]
\[ \ddot{x}(t) = \lambda^2 \cdot e^{\lambda t} \]
Jetzt können wir den Ansatz und seine Ableitungen in die Differentialgleichung einsetzen:
\[ m \cdot \lambda^2 e^{\lambda t} + b \cdot \lambda e^{\lambda t} + k \cdot e^{\lambda t} = 0 \]
\[ \Big (m \lambda^2 + b \lambda + k \Big) \cdot e^{\lambda t} = 0 \]
Der ausgeklammerte Term \(e^{\lambda t}\) kann unmöglich null sein, d.h. nur der Term in der Klammer kann null sein, um die Gleichung zu erfüllen. Das Ganze reduziert sich somit auf eine quadratische Gleichung:
\[ m \lambda^2 + b \lambda + k = 0 \]
\[ \lambda_{1,2} = \frac{-b \pm \sqrt{D}}{2m} \quad \text{mit} \quad D = b^2-4mk \]
Der Wert \(D\) wird Diskriminante genannt. Es gibt hier drei Fälle, die wir unterscheiden müssen:
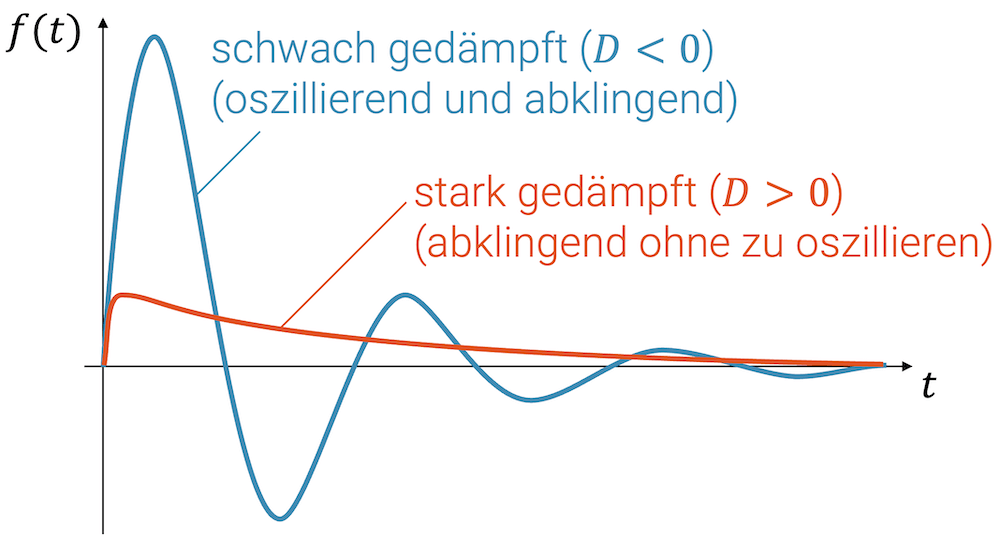
- \(D>0\) Bei starker Dämpfung (\(b\) gross) nennen wir das System stark gedämpft, so dass es nicht einmal mehr überschwingen und somit nicht oszillieren kann. Das ist z.B. bei einem Türdämpfer der Fall
- \(D=0\) entspricht dem Grenzfall
- \(D<0\) ergibt komplexe Lösungen \(\lambda \in \mathbb{C}\) und in Kombination mit der Exponentialfunktion gibt es die trigonometrischen Funktionen \(\sin\) und \(\cos\). Das System ist schwach gedämpft und oszilliert, jedoch mit abklingender Amplitude.

publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.