Sammellinse

Sammellinsen sind Scheiben mit gekrümmten Oberflächen aus einem transparenten Material (typischerweise aus Glas). Sammellinsen sind Linsen, die so geformt sind, dass sie in der Mitte dicker sind als aussen (konvex bzw. bikonvex). Durch die Brechung werden die Lichtstrahlen in der Sammellinse umgelenkt: Wenn parallele Strahlen (z.B. Sonnenstrahlen) senkrecht auf die Sammellinse treffen, werden sie hinter der Linse im Brennpunkt F gebündelt (“gesammelt”). Durch dieses Aufkonzentrieren von Sonnenstrahlung in einem sehr kleinen Punkt, können hohe Energiedichten erreicht werden, die brennbares Material entzünden können.

Sammellinsen finden wir in unseren Augen, in Lupen, Mikroskopen und Teleskopen, aber auch z.B. in Strahlern, Scheinwerfern und Taschenlampen. Brillengläser oder Kontaktlinsen für Weitsichtige sind ebenfalls ganz dünne Sammellinsen.

Mit Hilfe von Sammellinsen können reelle oder virtuelle Bilder erzeugt werden, die z.T. auch vergrössert sind (Bsp. Lupe, Mikroskop). Die Position des Bildes (Bildweite \(b\)) errechnet sich mit der Linsengleichung aus der Gegenstandsweite \(g\) und der Brennweite \(f\) der Linse:

\[ \frac{1}{f} = \frac{1}{g} + \frac{1}{b} \]

Strahlenverlauf

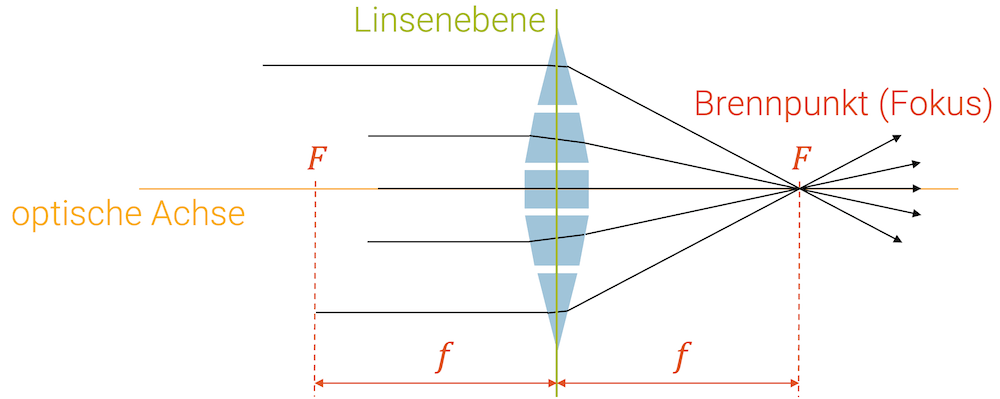
Wir stellen uns vor, dass die Sammellinse aus vielen trapezförmigen Prismen zusammengesetzt ist. Dank dem Brechungsgesetz verstehen wir, dass die parallelen Strahlen gegen die optische Achse umgelenkt werden. Nur der Lichtstrahl auf der optischen Achse trifft genau senkrecht auf das Medium der Linse und behält deshalb seine Richtung. Sammellinsen sind so geformt, dass die parallelen Strahlen alle im Brennpunkt F zusammenkommen.

Da wir in Optik die Zeit immer umkehren können, gilt auch: Brennpunktstrahlen, d.h. Lichtstrahlen, die durch den Brennpunkt der Sammellinse verlaufen, werden nach der Sammellinse zu Parallelstrahlen umgelenkt.

Sammellinsen haben immer zwei Brennpunkte, die auf der optischen Achse und im gleichen Abstand von der Linsenebene liegen (Brennweite \(f\)). 

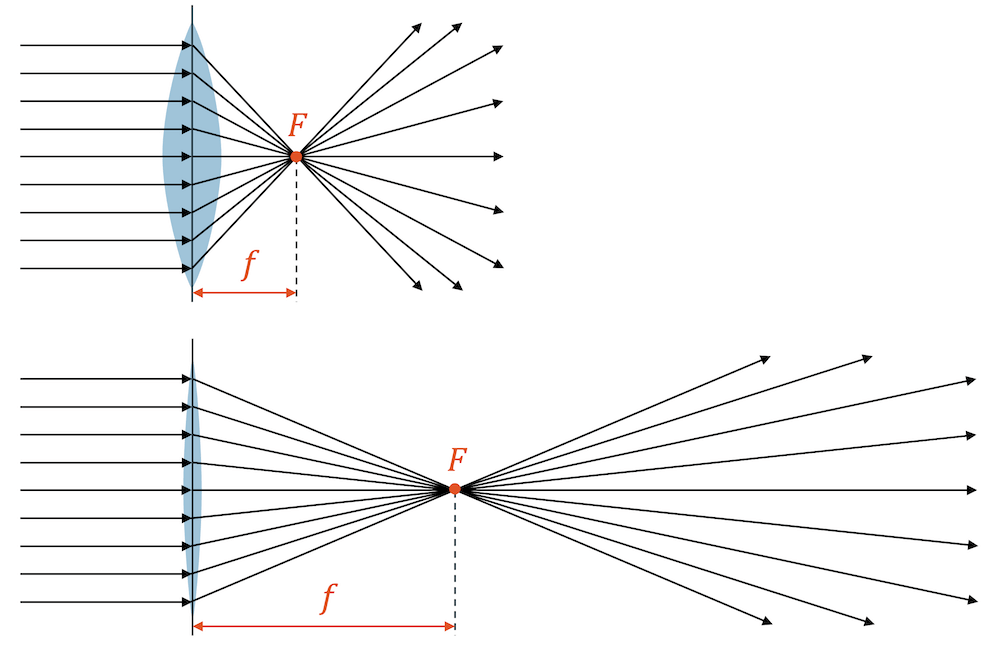
Der Abstand der Linsenebene vom Brennpunkt wird als Brennweite \(f\) bezeichnet. Dicke, bauchige Linsen brechen die Strahlen stark, so dass sie sich schon bald nach der Linse im Brennpunkt treffen. Sie haben eine kurze Brennweite.

Flache Linsen brechen die Strahlen nur schwach, so dass sie nach der Linse fast parallel verlaufen. Der Brennpunkt liegt deshalb weit von der Linse entfernt. Flache Linsen haben grosse Brennweiten.

Wichtigste Strahlen

Parallelstrahl \(^ \rightarrow\) Brennpunktstrahl

Brennpunktstrahl \(^ \rightarrow\) Parallelstrahl

Mittelpunktstrahl \(^ \rightarrow\) Mittelpunktstrahl

Bilder der Sammellinse

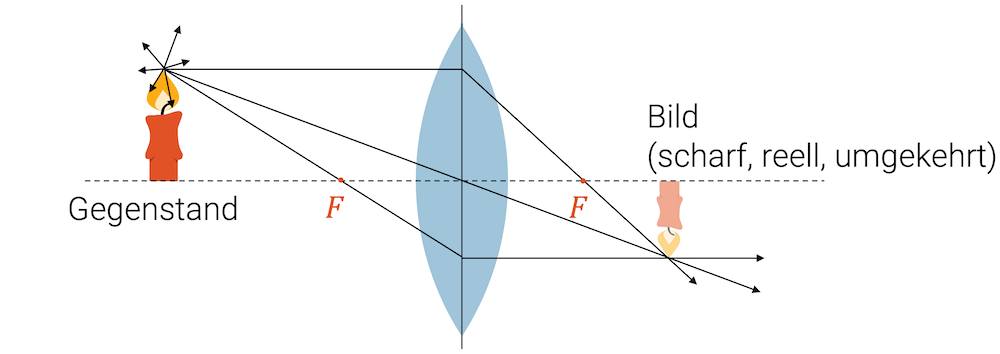
Die Spitze des Gegenstands sendet Lichtstrahlen (z.B. durch Streuung) in alle Richtungen. Wir betrachten drei spezielle Strahlen: Den Parallelstrahl (parallel zur optischen Achse), den Mittelpunktstrahl und den Brennpunktstrahl.

Beachte: Es ist in der Optik üblich, die Brechung an den beiden Linsenoberflächen nur mit einer einzige Brechung in der Linsenebene darzustellen. Oft wird der Linsenkörper gar nicht gezeichnet.

Wir wissen, dass der Parallelstrahl nach der Linse durch den Brennpunkt führt. Genauso muss der Brennpunktstrahl nach der Linse parallel werden. Der Mittelpunktstrahl wird nicht gebrochen. Konstruiert man diese drei Strahlen, stellt man fest, dass sie sich alle in einem Bildpunkt treffen. Es handelt sich um die Spitze des Bildes unseres Gegenstands.

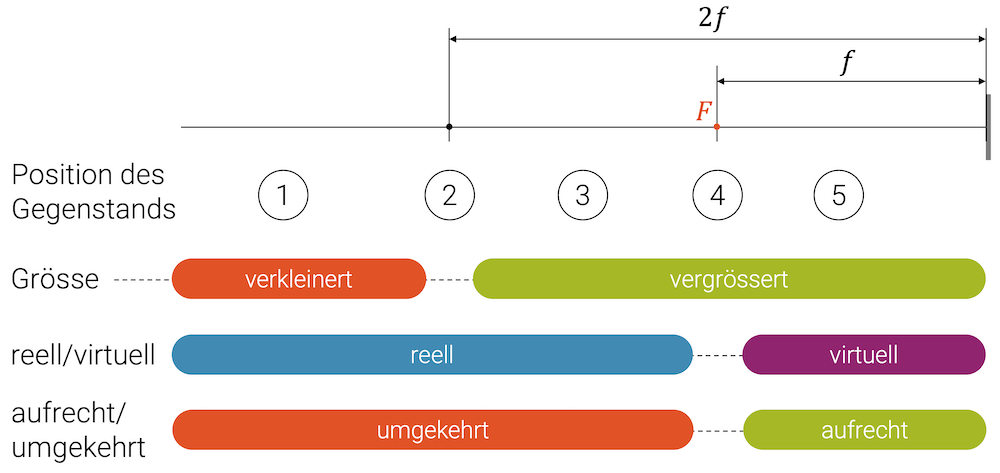
Da die Lichtstrahlen in diesem Bildpunkt physikalisch existieren, handelt es sich um ein reelles Bild. Weil sich der Bildpunkt unter der optischen Achse befindet, spricht man von einem umgekehrten reellen Bild. Je nach Position des Gegenstands gegenüber dem Brennpunkt, kann das Bild verkleinert oder vergrössert sein.

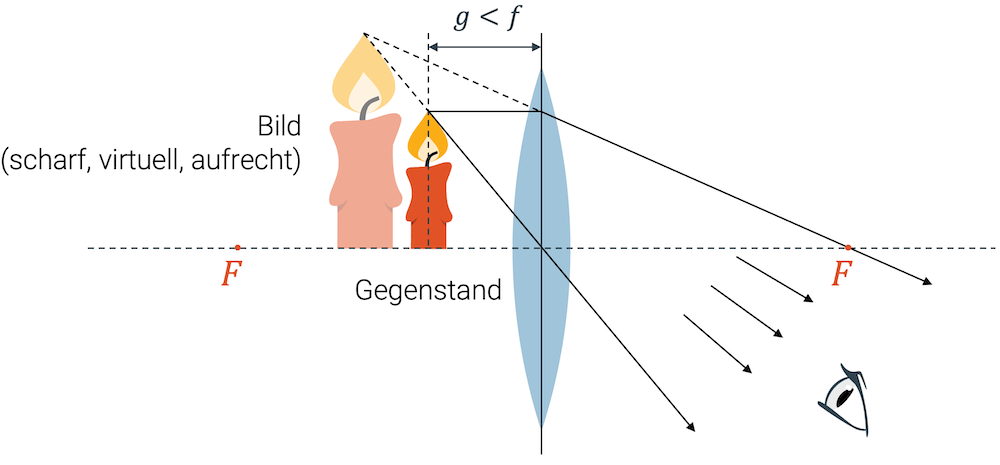
Liegt der Gegenstand zwischen Brennpunkt und Linsenebene, entsteht ein virtuelles Bild. Der Parallelstrahl wird nach der Linse wieder zu einem Brennpunktstrahl und der Mittelpunktstrahl bleibt ungebrochen. Die Strahlen divergieren nach der Linse, d.h. sie verlaufen auseinander und können sich somit nicht in einem Bildpunkt treffen.

Ein Betrachter (nach der Linse) könnte diese beiden Lichtstrahlen sehen und würde annehmen, dass sie gerade verlaufen. Die beiden gestrichelten Verlängerungen der Lichtstrahlen treffen sich vor der Linse in einem virtuellen Bildpunkt, der die Spitze des Bildes ausmacht. Das Bild ist virtuell, da die beiden Lichtstrahl im Bildpunkt nicht physisch vorkommen. Der Betrachter meint nur, sie kämen aus diesem gemeinsamen Punkt. Tatsächlich entstammen sie aber von der Spitze des Gegenstands, die aber anderswo ist.

Die Konstellation eines Gegenstands, das in sehr kleinem Abstand (näher als der Brennpunkt) durch eine Sammellinse betrachtet wird, entspricht der Verwendung einer Lupe.

Das Bild ist vergrössert und steht aufrecht. Wenn du eine Lupe verwendest, hältst du die Lupe so nahe an den Gegenstand heran, dass er zwischen Brennpunkt und Linsenebene zu liegen kommt. Wenn du mit der gleichen Lupe in die Ferne schaust, siehst du die Welt auf dem Kopf, da wir dann eine Gegenstandsweite haben, die wieder grösser ist als die Brennweite und wir somit wieder ein reelles, umgekehrtes Bild erhalten.

Es ist eine besondere Eigenart von Sammellinsen, je nach Gegenstandsweite zwischen umgekehrtem und aufrechtem Bild zu wechseln. Beobachtet man ein “Umkippen” des Bildes wenn der Abstand des Gegenstands verändert wird, handelt es sich um eine Sammellinse. Streulinsen haben diese Eigenschaft nicht. Der Abstand im Kipppunkt ist gleichzeitig auch die Brennweite der Linse.

Linsenabbildungen bei der Sammellinse

Gegenstandsweite \(g\)	Bildweite \(b\)	Bildgrösse \(B\)	Bildausrichtung	Bildart
\(g > 2f\)  weiter als \(2f\) entfernt	\(f < b < 2f\)  zwischen einfacher und doppelter Brennweite	\(B < G\)  verkleinert	umgekehrt	reell
\(g = 2f \(  genau \(2f\) entfernt	\(b = 2f\)  genau \(2f\) entfernt	\(B = G\)  gleich gross	umgekehrt	reell
\(f < g < 2f\)  zwischen einfacher und doppelter Brennweite	\(b > 2f\)  weiter als \(2f\) entfernt	\(B > G\)  vergrössert	umgekehrt	reell
\(g = f\)	(Kipppunkt: kein Bild)
\(0 < g < f\) | \(b > g\)	\(B > G\)  vergrössert		aufrecht	virtuell

Linsengleichung

Mit der Linsengleichung werden die Gegenstandsweite \(g\), die Brennweite \(f\) und die Bildweite \(b\) mit einander verknüpft, d.h. Du kannst berechnen wo das Bild hinter der Linse mit Brennweite \(f\) entsteht, wenn der Gegenstand in einem bestimmten Abstand \(g\) vor der Linse steht:

\[ \frac{1}{f} = \frac{1}{g} + \frac{1}{b} \]

Beispiel

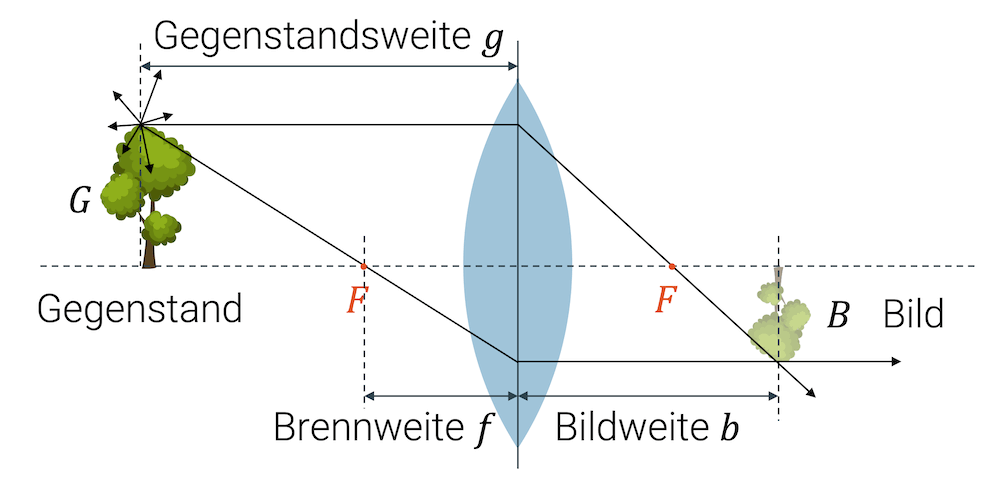
Ein \(10\,\mathrm{m}\) hoher Baum steht im Abstand \(g=20\,\mathrm{m}\) vor einer Sammellinse mit Brennweite \(f=20\,\mathrm{cm}\).

Wo müssen wir ein weisses Blatt Papier hinter der Linse hinhalten, um das scharfe Bild zu sehen und wie gross ist das Bild?

---

Mit der Linsengleichung erhalten wir:

\[ \frac{1}{b} = \frac{1}{f} – \frac{1}{g} = \frac{1}{0.2\,\mathrm{m}} – \frac{1}{20\,\mathrm{m}} = 5\,\mathrm{m^{-1}} – 0.05\,\mathrm{m^{-1}} = 4.95\,\mathrm{m^{-1}} \]

Nun bilden wir den Kehrwert von \(\frac{1}{b}\) und erhalten:

\[ b = \frac{1}{4.95\,\mathrm{m^{-1}}} = 0.202\,\mathrm{m} = 20.2\,\mathrm{cm} \]

Um die Grösse des Bildes \(B\) zu berechnen, benutzen wir den Mittelpunktstrahl und wenden den Strahlensatz an. Der Baum erzeugt ein rechtwinkliges Dreieck mit der Höhe \(G=10\,\mathrm{m}\). Rechts erzeugt das Bild ein ähnliches Dreieck mit der Höhe \(B\). Der Strahlensatz besagt, dass die Seitenlängen in ähnlichen Dreiecken zueinander proportional sind. Wir können deshalb schreiben:

\[ \frac{G}{g} = \frac{B}{b} \]

Wir lösen nach der unbekannten Bildhöhe \(B\) auf und setzen die Werte ein:

\[ B = \frac{b}{g} \cdot G = \frac{0.202\,\mathrm{m}}{20\,\mathrm{m}} \cdot 10\,\mathrm{m} = 0.101\,\mathrm{m} = \underline{10.1\,\mathrm{cm}} \]

Herleitung Linsengleichung

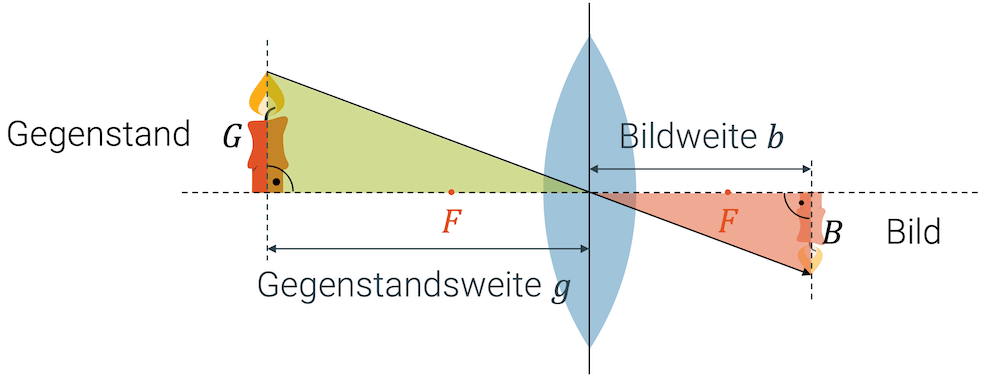
Wenn wir den Mittelpunktstrahl einzeichnen, erhalten wir zwei ähnliche, rechtwinklige Dreiecke. Aus der Ähnlichkeit folgt, dass die Längenverhältnisse gleich sind und wir den Strahlensatz anwenden können:

\[ \frac{G}{g} = \frac{B}{b} \quad \mathrm{bzw.} \quad \frac{B}{G} = \frac{b}{g} \]

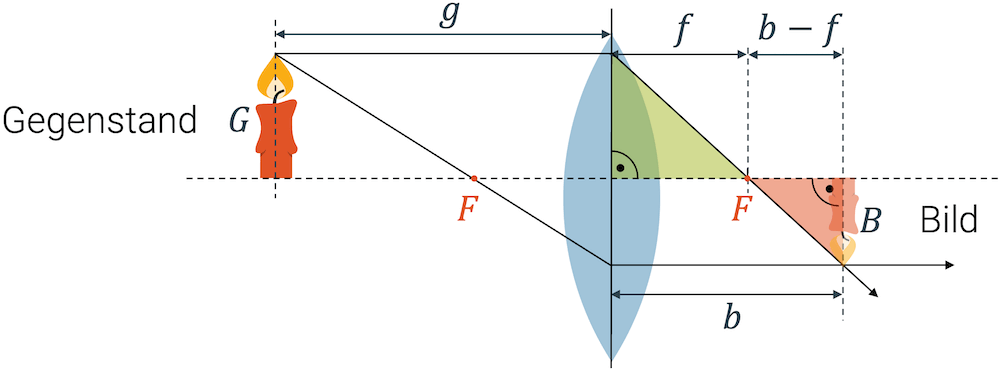
Nun betrachten wir den Brennpunktstrahl nach der Linse. Die beiden markierten rechtwinkligen Dreiecke haben die gleichen Winkel und sind dadurch auch geometrisch ähnlich, d.h. ihre Seitenlängen stehen im gleichen Verhältnis:

\[ \frac{G}{f} = \frac{B}{b-f} \]

Wir dividieren durch \(B\) und multiplizieren mit \(f\):

\[ \frac{G}{B} = \frac{f}{b-f} \]

Nun bilden wir den Kehrwert der Gleichung:

\[ \frac{B}{G} = \frac{b-f}{f} = \frac{b}{f} – 1 \]

Links setzen wir die erste Gleichung für den Ausdruck \(\frac{B}{G}\) ein und erhalten:

\[ \frac{b}{g} = \frac{b}{f} – 1 \]

Division durch \(b\) führt zu:

\[ \frac{1}{g} = \frac{1}{f} – \frac{1}{b} \quad \mathrm{bzw.} \quad \frac{1}{f} = \frac{1}{b} + \frac{1}{g} \]

Simulation

Bewege die Spitze des Gegenstands Object mit der Maus. Der Brennpunkt wird verändert, indem du das Label Focus‘ verschiebst.

• Simulation der Strahlenverläufe durch eine Sammel- bzw. Streulinse