Videos
Wir können zu einem Vektor, z.B. \(\vec{c}\), immer ein Paar von zwei Vektoren finden, die wir jetzt \(\vec{a}\) und \(\vec{b}\) nennen. Addieren wir die beiden Vektoren \(\vec{a}\) und \(\vec{b}\), kriegen wir den Summenvektor \(\vec{c}\):
\[ \vec{a} + \vec{b} = \vec{c} \]
Wir kehren die Addition um: Wir starten mit der Summe und finden zwei Summanden, die diese Summe ergeben.
Jetzt gibt es aber nicht nur ein solches Vektorenpaar, sondern unendlich viele Kombinationen. Genau wie wir 1+1=2, aber auch 1.5 + 0.5 = 2 oder 1.1 + 0.9 = 2 usw. schreiben könnten.
Allen Vektorenpaaren gemeinsam ist, dass jedes Vektorenpaar ein Parallelogramm aufspannt.
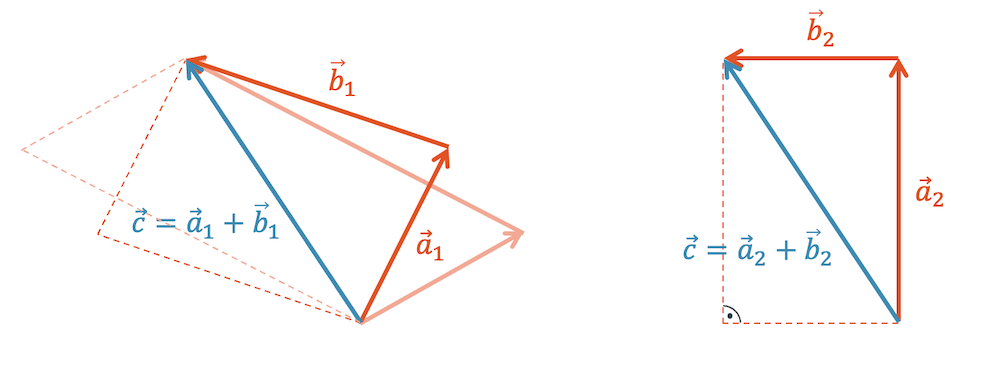
Von besonderem Interesse ist dabei das Vektorenpaar, das ein Rechteck bildet, wie rechts im Bild. Es ist auch ein Parallelogramm, hat aber einen rechten Winkel. Das wird uns in Zukunft sehr behilflich sein, denn rechte Winkel sind für Berechnungen immer sehr praktisch.
Jeder Vektor kann in zwei neue Vektoren zerlegt werden, so dass die beiden neuen Vektoren in Summe wieder den ersten Vektor ergeben.
Aus der Richtung der beiden Vektoren kann ein Parallelogramm gebildet werden. Der zu zerlegen- de Vektor bildet die eine der beiden Diagonalen des Parallelogramms.
Besonders praktisch ist das Rechteck, weil es mit seinem rechten Winkel für Berechnungen viel einfacher ist.
Beispiel
Finde zu folgendem Vektor \(\vec{c}\) zwei einfache Vektoren \(\vec{a}\) und \(\vec{b}\), so dass gilt:
\[ \vec{c} = \vec{a} + \vec{b} \]
Zeichne die beiden Vektoren unten ein.
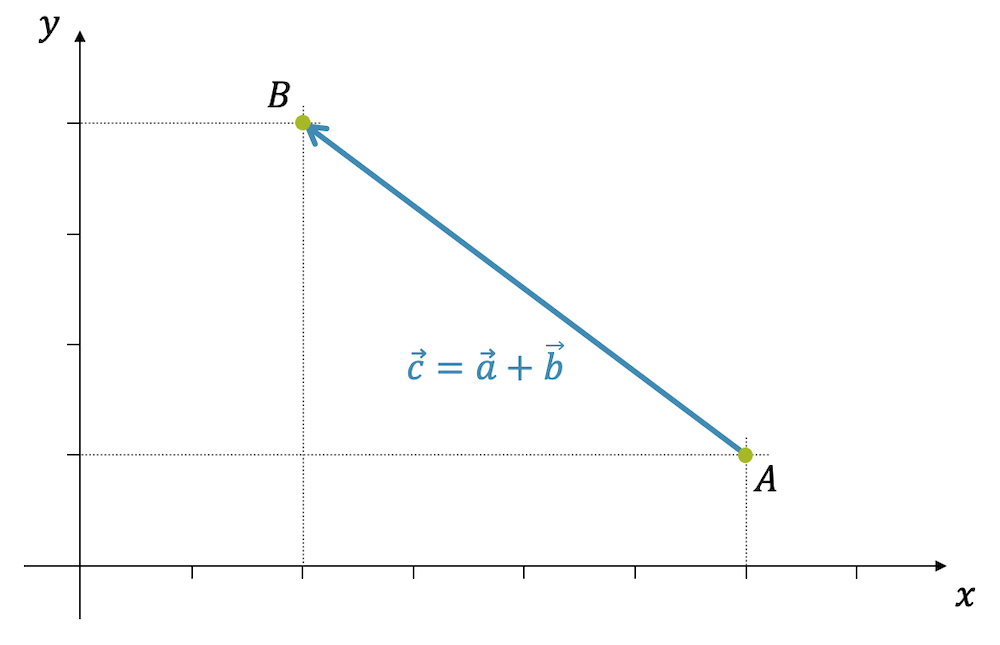
Am einfachsten ist wohl die Verschiebung in \(x\)- und \(y\)-Richtung in zwei Schritten zu machen. Wir können z.B. zuerst vom Punkt \(A\) aus nach oben gehen und dann nach links. Das gibt uns zwei Vektoren \(\vec{a}\) und \(\vec{b}\):
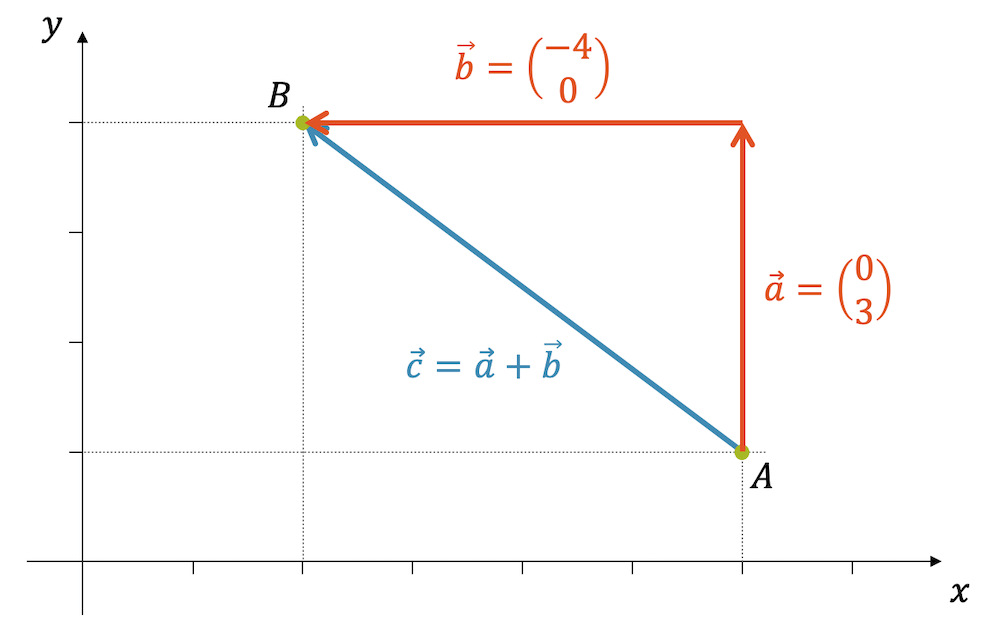
Die Komponenten der beiden Vektoren sind leicht abzulesen. Wir haben schon die Lösung:
\[ \underline{\vec{a} = \begin{pmatrix} 0 \\ 3 \end{pmatrix}} \qquad \qquad \underline{\vec{b} = \begin{pmatrix} -4 \\ 0 \end{pmatrix}} \]
Jetzt kontrollieren wir aber, ob deren Summe auch wirklich den Vektor \(\vec{c}\) ergibt:
\[ \vec{a} + \vec{b} = \begin{pmatrix} 0 \\ 3 \end{pmatrix} + \begin{pmatrix} -4 \\ 0 \end{pmatrix} = \begin{pmatrix} 0-4 \\ 3+0 \end{pmatrix} \]
\[ \vec{a} + \vec{b} = \begin{pmatrix} -4 \\ 3 \end{pmatrix} \]
Den Vektor \(\vec{c}\) können wir ablesen oder als Vektor \(\overrightarrow{AB}\) bestimmen, der den Punkt \(A(6,1)\) zum Punkt \(B(2,4)\) abbildet:
\[ \vec{c} = \overrightarrow{AB} = \begin{pmatrix} 2-6 \\ 4-1 \end{pmatrix} = \begin{pmatrix} -4 \\ 3 \end{pmatrix} \]
Tatsächlich haben wir wieder den gleichen Vektor erhalten.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.