Gleichung eines Kreises

Ein Kreis ist eine Punktschar mit unendlich vielen Punkten, die alle eine gemeinsame Eigenschaft haben. Sie sind alle gleich weit von einem bestimmten Punkt entfernt, nämlich dem Zentrum \(Z\) des Kreises. Der für alle Kreispunkte gleiche Abstand vom Zentrum heisst Radius \(r\).

Schauen wir uns ein Beispiel an: Das Zentrum hat die Koordinaten \(Z(2,3)\) und der Radius ist \(r=2\), wie wir aus der Abbildung entnehmen können. Die Punkte \(A\), \(B\) und \(Q\) liegen auf dem Kreis \(k\).

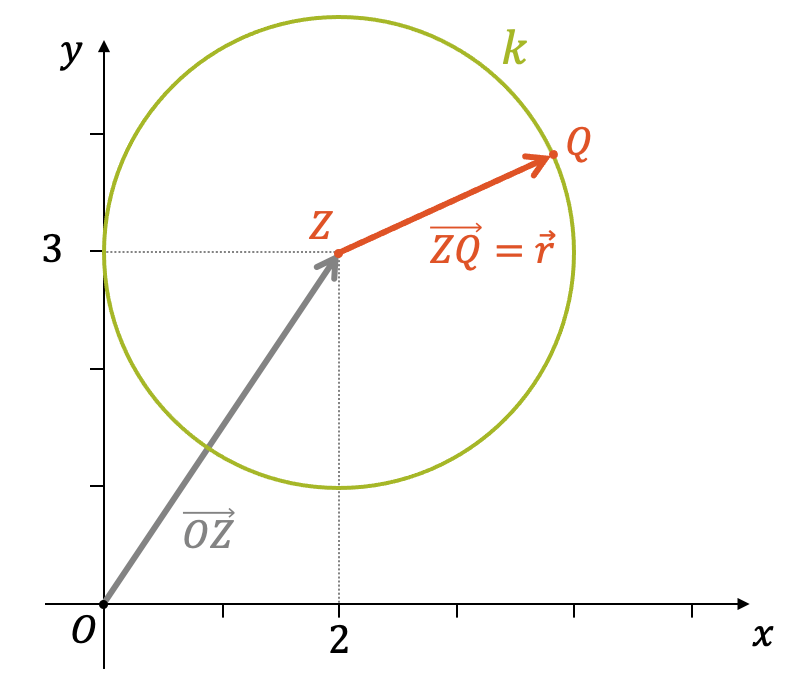
Wie können wir diese Punkte auf \(k\) mathematisch beschreiben? Wir erhalten mit Hilfe der Vektorschreibweise einen Ausdruck für den Vektor \(\overrightarrow{ZQ}\):

\[ \overrightarrow{OQ} = \overrightarrow{OZ} + \overrightarrow{ZQ} \]

\[ \rightarrow \quad \overrightarrow{ZQ} = \overrightarrow{OQ} – \overrightarrow{OZ} \]

Der Ortsvektor des Zentrums \(\overrightarrow{OZ}\) enthält in Komponentenschreibweise die Koordinaten des Zentrums: \(\overrightarrow{OZ} = \begin{pmatrix} Z_x \\ Z_y \end{pmatrix}\), während der Ortsvektor \(\overrightarrow{OQ}\) die Koordinaten aller Punkte \(Q\) auf dem Kreis enthält. Hierfür schreiben wir einfach \(x\) und \(y\): \(\overrightarrow{OQ} = \begin{pmatrix} x \\ y \end{pmatrix}\). Somit ist der Vektor \(\overrightarrow{ZQ}\) in Komponentenschreibweise:

\[ \overrightarrow{ZQ} = \begin{pmatrix} x \\ y \end{pmatrix} – \begin{pmatrix} Z_x \\ Z_y \end{pmatrix} = \begin{pmatrix} x – Z_x \\ y – Z_y \end{pmatrix} \]

Von diesem Vektor \(\overrightarrow{ZQ}\), der die Rolle des Radius übernimmt, kennen wir ja die Länge:

\[ \Big| \overrightarrow{ZQ} \Big| = \sqrt{(ZQ_x)^2 + (ZQ_y)^2} = r \]

Um die Wurzel los zu werden, quadrieren wir einfach:

\[ (ZQ_x)^2 + (ZQ_y)^2 = r^2 \]

Die Summe der Quadrate seiner Komponenten ist gleich dem Quadrat des Radius, d.h.

\[ (x – Z_x)^2 + (y – Z_y)^2 = r^2 \]

In unserem Fall erhalten wir mit \(Z(2,3)\), d.h. \(Z_x=2\) und \(Z_y=3\) und \(r=2\) die Gleichung in Koordinatenform für unseren Kreis \(k\):

\[ (x – 2)^2 + (y – 3)^2 = 4 \]

Beispiel

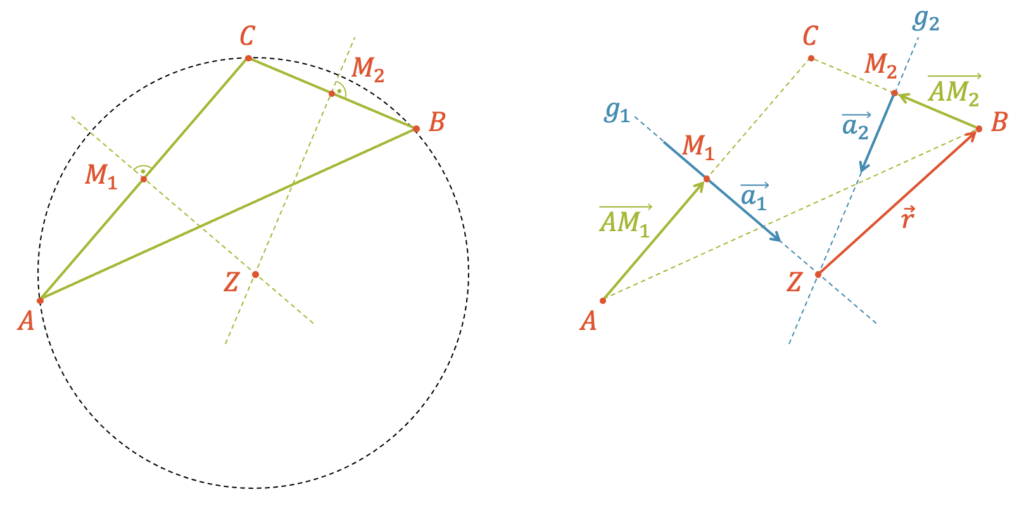
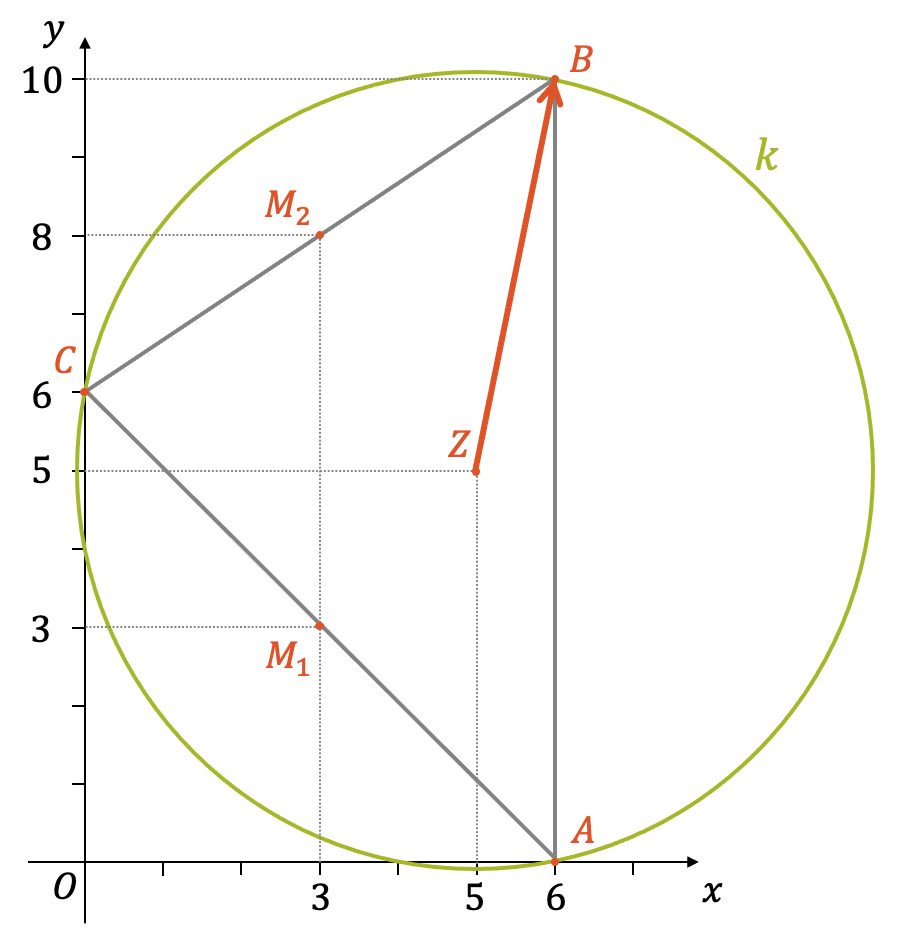
Finde für das Dreieck \(ABC\) mit \(A(6,0)\), \(B(6,10)\) und \(C(0,6)\) die Gleichung seines Umkreises.

Tipp: Mache zuerst eine Skizze und einen Plan, wie du die Aufgabe mit Vektorgeometrie lösen willst.

---

Wir machen eine Skizze von einem beliebigen Dreieck \(ABC\) und zeichnen seinen Umkreis. Jetzt überlegen wir uns, wie wir zum Zentrum \(Z\) finden.

Für das Aufstellen der Kreisgleichung brauchen wir die Koordinaten des Kreiszentrums und den Radius. Den Radius erhalten wir schnell, wenn wir das Kreiszentrum kennen. Die eigentlich Schwierigkeit ist also das Zentrum \(Z\) zu finden.

Wir erinnern uns an die Geometrie, die besagt, dass das Zentrum eines Umkreises im Schnittpunkt der Mittelsenkrechten liegt. Wie kommen wir dahin? Um eine Aufgabe in der Art zu lösen, müssen zuerst Überlegungen gemacht werden, wie die Folgenden. Damit wird die Aufgabe eigentlich gelöst. Der Rest ist nur noch pures Rechnen.

Für die Mittelsenkrechte brauchen wir erst mal den Mittelpunkt auf der Dreiecksseite. Mit den Koordinaten der Ecken haben wir die Vektoren für die Seiten, z.B. \(\overrightarrow{AC}\) und \(\overrightarrow{BC}\). Einen Vektor zu halbieren ist auch nicht schwer. Wir multiplizieren ihn einfach mit dem Faktor \(\frac{1}{2}\):

\[ \overrightarrow{AM_1} = \frac{1}{2} \cdot \overrightarrow{AC} \]

\[ \overrightarrow{AM_2} = \frac{1}{2} \cdot \overrightarrow{BC} \]

Mit Hilfe dieser beiden Vektoren erhalten wir die Mittelpunkte \(M_1\) und \(M_2\) auf den Dreiecksseiten indem wir von der einen Ecke starten:

\[ \overrightarrow{OM_1} = \overrightarrow{OA} + \overrightarrow{AM_1} \]

\[ \overrightarrow{OM_2} = \overrightarrow{OB} + \overrightarrow{AM_2} \]

Jetzt haben wir die Koordinaten der Punkte \(M_1\) und \(M_2\). Sie sind die Stützpunkte der Mittelsenkrechten \(g_1\) und \(g_2\), für die wir die Geradengleichung aufstellen können. Dazu braucht es je einen Stützpunkt und einen Richtungsvektor \(\vec{a_1}\) bzw. \(\vec{a_2}\). Der Richtungsvektor muss natürlich senkrecht zum Vektor \(\overrightarrow{AM_1}\) bzw. \(\overrightarrow{AM_2}\) sein. Das kriegen wir mit dem Trick: Komponenten tauschen und bei einer Komponente das Vorzeichen wechseln:

\[ \overrightarrow{AM_1} \rightarrow \vec{a_1} \rightarrow g_1 \]

\[ \overrightarrow{AM_2} \rightarrow \vec{a_2} \rightarrow g_2 \]

Nun lassen wir die beiden Geradengleichungen von \(g_1\) und \(g_2\) sich schneiden. Die Vektorgleichung gibt uns ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten, den beiden Parametern der Geradengleichung \(\lambda_1\) und \(\lambda_2\). Die eine Lösung für diese Parameter gibt uns den Faktor, so dass wir auf der entsprechenden Gerade genau zum Schnittpunkt gelangen, d.h. wir kriegen die Koordinaten von \(Z\).

Jetzt braucht es nur noch den Radius. Er ist der Abstand von \(Z\) zu einer Dreiecksecke, z.B. \(B\):

\[ r = \big| \overrightarrow{ZB} \big| \]

Mit den Koordinaten des Punktes \(Z\) und dem Radius \(r\) haben wir alles, was wir für das Aufstellen der Kreisgleichung brauchen.

Wir stellen zuerst die Gleichung der Geraden \(g_1\) für die erste Mittelsenkrechte auf:

\[ \overrightarrow{AM_1} = \frac{1}{2} \cdot \overrightarrow{AC} = \frac{1}{2} \cdot \begin{pmatrix} 0-6 \\ 6-0 \end{pmatrix} = \begin{pmatrix} -3 \\ 3 \end{pmatrix} \]

\[ \overrightarrow{OM_1} = \overrightarrow{OA} + \overrightarrow{AM_1} = \begin{pmatrix} 6-3 \\ 0+3 \end{pmatrix} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} \]

\[ \overrightarrow{AM_1} = \begin{pmatrix} -3 \\ 3 \end{pmatrix} \quad \rightarrow \quad  \vec{a_1} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} \]

\[ \rightarrow \quad g_1 \colon \;\; \begin{pmatrix} 3 \\ 3 \end{pmatrix} + \lambda_1 \cdot \begin{pmatrix} 3 \\ 3 \end{pmatrix}\]

In gleicher Art erhalten wir die Gleichung der Geraden \(g_2\) für die zweite Mittelsenkrechte:

\[ \overrightarrow{AM_2} = \frac{1}{2} \cdot \overrightarrow{BC} = \frac{1}{2} \cdot \begin{pmatrix} 0-6 \\ 6-10 \end{pmatrix} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} \]

\[ \overrightarrow{OM_2} = \overrightarrow{OB} + \overrightarrow{AM_2} = \begin{pmatrix} 6-3 \\ 10-2 \end{pmatrix} = \begin{pmatrix} 3 \\ 8 \end{pmatrix} \]

\[ \overrightarrow{AM_2} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} \quad \rightarrow \quad  \vec{a_2} = \begin{pmatrix} 2 \\ -3 \end{pmatrix} \]

\[ \rightarrow \quad g_2 \colon \;\; \begin{pmatrix} 3 \\ 8 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 2 \\ -3 \end{pmatrix}\]

Jetzt setzen wir die beiden gleich und erhalten ein Gleichungssystem:

\[ \begin{pmatrix} 3 \\ 3 \end{pmatrix} + \lambda_1 \cdot \begin{pmatrix} 3 \\ 3 \end{pmatrix} \;\; \stackrel{!}{=} \;\; \begin{pmatrix} 3 \\ 8 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 2 \\ -3 \end{pmatrix} \]

\[ \begin{cases} \begin{array}{cc} 3 \lambda_1 – 2 \lambda_2 \;\; = \;\; 0 \\ 3 \lambda_1 + 3 \lambda_2 \;\; = \;\; 5 \\ \end{array} \end{cases} \]

Eine Lösung des Gleichungssystems reicht aus. Wir subtrahieren die zweite Gleichung von der Ersten und erhalten die Lösung für \(\lambda_2\). Mit Hilfe dieses Parameters erhalten wir den Schnittpunkt \(Z\) der beiden Geraden.

\[ \lambda_2 = 1 \]

\[ \rightarrow \quad \overrightarrow{OZ} = \begin{pmatrix} 3 \\ 8 \end{pmatrix} + 1 \cdot \begin{pmatrix} 2 \\ -3 \end{pmatrix} = \begin{pmatrix} 5 \\ 5 \end{pmatrix} \]

Den Radius \(r\) erhalten wir aus der Länge von \(Z\) zu einer der drei Ecken:

\[ \overrightarrow{ZB} = \begin{pmatrix} 6-5 \\ 10-5 \end{pmatrix} = \begin{pmatrix} 1 \\ 5 \end{pmatrix} \]

\[ \rightarrow \quad r = \big| \overrightarrow{ZB} \big| = \sqrt{1^2 + 5^2} = \sqrt{26} \]

\[ \underline{k \colon \;\; (x-5)^2 + (y-5)^2 = 26} \]