Sammellinse

Sammellinsen sind linsenförmig, d.h. sie sind in der Mitte dicker sind als aussen (konvex bzw. bikonvex). Durch Brechung werden Lichtstrahlen an der Grenzfläche umgelenkt, bei Eintritt und bei Austritt aus der Linse.

Sammellinsen finden wir in unseren Augen, in Lupen, Mikroskopen und Teleskopen, aber auch z.B. in Strahlern, Scheinwerfern und Taschenlampen. Brillengläser oder Kontaktlinsen für Weitsichtige sind ebenfalls ganz dünne Sammellinsen.

Die Natur macht auch Sammellinsen, meistens in Form von mehr oder weniger kugelförmigen Tropfen. Das können grosse Tautropfen sein, wie im folgenden Bild oder kleinste Tröpfchen in einer Wolke, die den Regenbogen bilden. 🌈

Brennpunkt und Brennweite einer Sammellinse

Wenn parallele Strahlen (z.B. Sonnenstrahlen) senkrecht auf die Sammellinse treffen, werden sie hinter der Linse im Brennpunkt \(F\) gebündelt (“gesammelt”). Durch dieses Aufkonzentrieren der Sonnenstrahlung in einem sehr kleinen Punkt, können hohe Energiedichten erreicht werden, die brennbares Material entzünden können.

Sammellinsen haben immer zwei Brennpunkte ✌️, die auf der optischen Achse und im gleichen Abstand links und rechts von der Linsenebene liegen (Brennweite \(f\)).

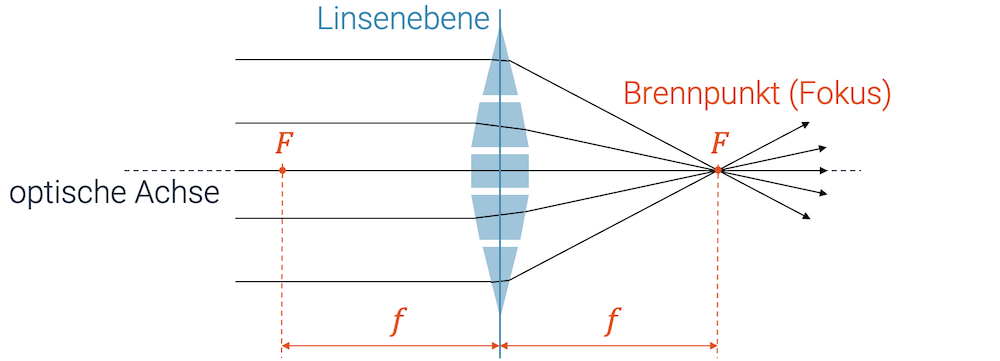
Wir stellen uns vor, dass die Sammellinse aus vielen trapezförmigen Prismen zusammengesetzt ist. Dank dem Brechungsgesetz verstehen wir, dass die parallelen Strahlen gegen die optische Achse umgelenkt werden. Nur der Lichtstrahl auf der optischen Achse trifft genau senkrecht auf das Medium der Linse und behält deshalb seine Richtung. Sammellinsen sind so geformt, dass die parallelen Strahlen alle im Brennpunkt \(F\) zusammenkommen:

Parallelstrahlen werden durch die Sammellinse umgelenkt zu Brennpunktstrahlen

Da wir in Optik die Zeit immer umkehren können, gilt auch:

Brennpunktstrahlen werden durch die Sammellinse umgelenkt zu Parallelstrahlen

Lichtstrahlen, die durch den Brennpunkt der Sammellinse verlaufen, verlaufen nach der Sammellinse parallel zur optischen Achse. Das wird z.B. bei Scheinwerfern ausgenutzt, denn parallele Strahlen behalten ihre Intensität, währenddem radiale Lichtquellen eine Intensität haben, die mit dem Abstand im Quadrat abfällt.

Je stärker die Umlenkung ist, desto näher liegt der Brennpunkt bei der Linse. Der Abstand der Linse zum Brennpunkt heisst Brennweite \(f\).

• starke Sammellinsen sind sehr bauchig, sie lenken stark um und haben eine kurze Brennweite \(f\)
• schwache Sammellinsen sind sehr flach, sie lenken schwach und haben eine kurze Brennweite \(f\)

Beachte: Eine flache Glasscheibe kann als Sammellinse mit unendlicher Brennweite (\(f \rightarrow \infty\)) betrachtet werden.

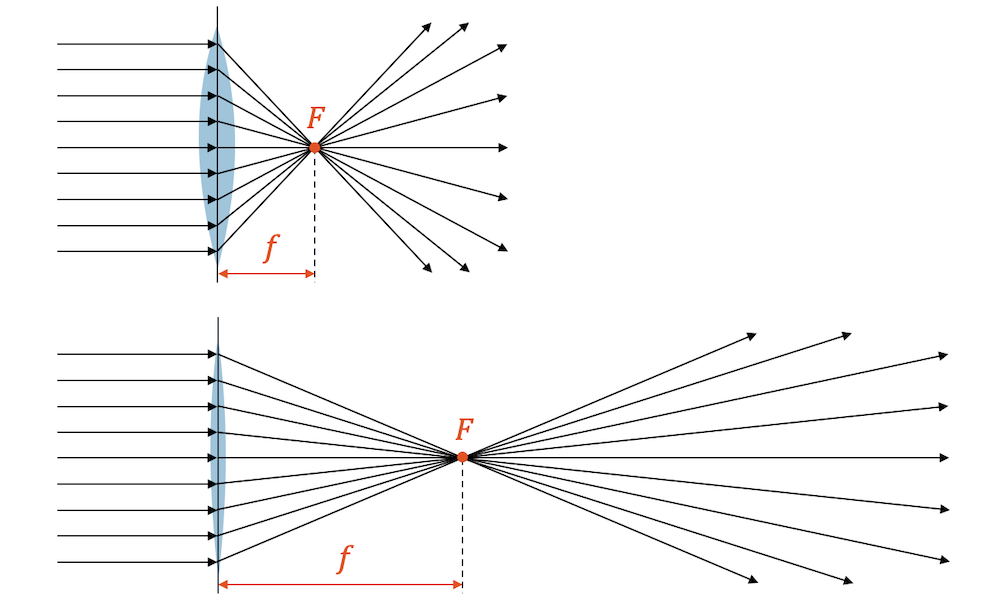
Beachte: Da die Linsen sehr dünn sind, werden die Strahlen nur bis zur Linsenebene gezogen und erst dort gebrochen. Die Form der Linse dient nur als Andeutung. Das ist eine wichtige Konvention, die wir schon bei den gewölbten Spiegeln kennengelernt haben.

Selbst wenn die Sammellinse nur auf einer Seite bauchig ist, hat sie die gleiche Brennweite auf beiden Seiten, d.h. die Strahlumlenkung ist unabhängig von der Ausrichtung oder Form der Sammellinse. Sie hängt nur von der Brennweite der Linse ab.

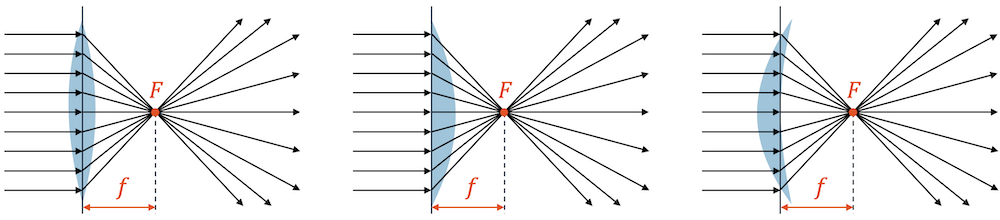
Die Unabhängigkeit der Ausrichtung der Linse kann auch mit der Zeitumkehrung verstanden werden. Lassen wir “den Film rückwärts laufen”, so gehen die Strahlen in der Optik den genau gleichen Weg zurück: Die Brennpunktstrahlen werden zu Parallelstrahlen. Das passiert wiederum unabhängig von der Ausrichtung der Linse. 👀

Entstehung eines reellen Bildes

Die ganz typische Eigenschaft der Sammellinsen ist die Bildung eines umgekehrten reellen Bilds. Das können nur Sammellinsen.

Die Tatsache, dass das Bild auf dem Kopf steht ist nicht unbedingt praktisch. Es ist aber für uns das Merkmal, das uns verrät, dass wir ein reelles Bild einer Sammellinse anschauen. Die Tatsache, dass das Bild reell ist, ist aus physikalischer Sicht schon interessanter!

Wenn wir nämlich die folgenden Regeln anwenden, erhalten wir einen Schnittpunkt mehrerer Strahlen, die zum gleichen Gegenstandspunkt gehören, d.h. wir haben in diesem Schnittpunkt einen Bildpunkt.

Parallelstrahlen werden durch die Sammellinse umgelenkt zu Brennpunktstrahlen

Brennpunktstrahlen werden durch die Sammellinse umgelenkt zu Parallelstrahlen

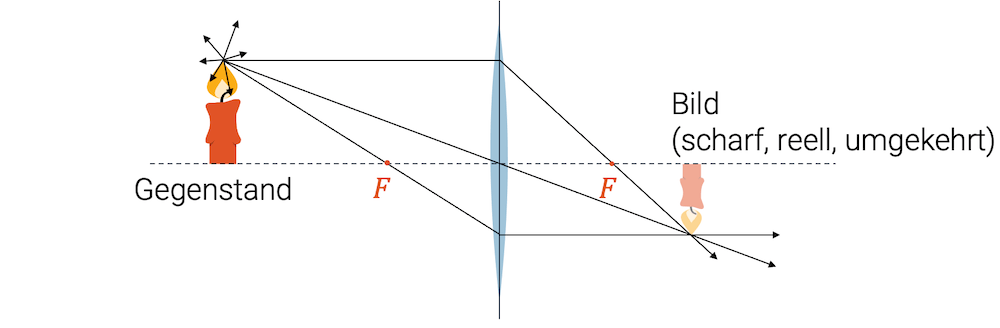
Die Flammenspitze sendet Lichtstrahlen in alle Richtungen. Wir betrachten hier drei spezielle Strahlen: Den Parallelstrahl (parallel zur optischen Achse), den Brennpunktstrahl (durch den Brennpunkt verlaufend) und den Scheitelpunktstrahl, der die Linse in der Mitte trifft (optische Achse).

Wir wissen, dass der Parallelstrahl nach der Linse durch den Brennpunkt führt. Genauso muss der Brennpunktstrahl nach der Linse parallel werden. Konstruiert man diese Strahlen, stellt man fest, dass sie sich in einem Bildpunkt treffen. Es handelt sich hier um den Bildpunkt der Flammenspitze.

Da die Lichtstrahlen in diesem Bildpunkt physikalisch existieren, handelt es sich um ein reelles Bild. Je nach Position des Gegenstands gegenüber dem Brennpunkt, kann das Bild verkleinert oder vergrössert sein.

In der obigen Grafik ist zusätzlich noch ein dritter Strahl gezeichnet, der Scheitelpunktstrahl, den du vermutlich vom Konkavspiegel kennst. Er wird oft auch Mittelpunktstrahl genannt, doch diese Bezeichnung wäre problematisch, wenn wir sie beim Konkavspiegel anwenden wollten, weil es dort einen anderen Strahl gibt, der so heisst.

Beim Konkavspiegel haben wir für den Scheitelpunktstrahl mit dem Reflexionsgesetz argumentiert und gesagt, dass er mit gleichem Winkel reflektiert wird (Reflexionswinkel), wie er auf den Spiegel eingefallen ist (Einfallswinkel).

Bei der Linse haben wir keine Reflexion, aber der Scheitelpunktstrahl ist sehr praktisch, weil einfach zu zeichnen. Er wird ungebrochen durch die Linsenebene gezeichnet. Er verhält sich analog zum Spiegel, d.h. er verlässt die Linsenebene in gleichem Winkel, wie er auf sie aufgetroffen ist.

Beachte, dass in Realität der Strahl durchaus parallel zum ursprünglichen Strahl verläuft, aber leicht versetzt ist. Die Dicke der Linse bestimmt, wie stark versetzt der Strahl ist. Da wir aber von sehr dünnen Linsen ausgehen, vernachlässigen wir diesen Effekt.

Entstehung eines virtuellen Bildes

Das reelle Bild ist eigentlich schon ziemlich verrückt, aber jetzt kann unsere Sammellinse auch noch ein virtuelles Bild erschaffen und das ist vergrössert!

Liegt der Gegenstand sehr nahe bei der Linse, genauer: zwischen Brennpunkt und Linsenebene, so entsteht ein virtuelles Bild. Die Gegenstandsweite \(g\) muss kleiner sein als die Brennweite der Linse \(f\):

\[ g < f \]

Um das Bild zu konstruieren, benutzen wir den Parallelstrahl und den Scheitelpunktstrahl. Den sonst sehr nützlichen Brennpunktstrahl können wir dieses Mal nicht gebrauchen, denn er verläuft ja weg von der Linse.

Der Parallelstrahl wird nach der Linse wieder zu einem Brennpunktstrahl und der Scheitelpunktstrahl bleibt ungebrochen. Wir erhalten zwei Strahlen, die auseinander gehen.

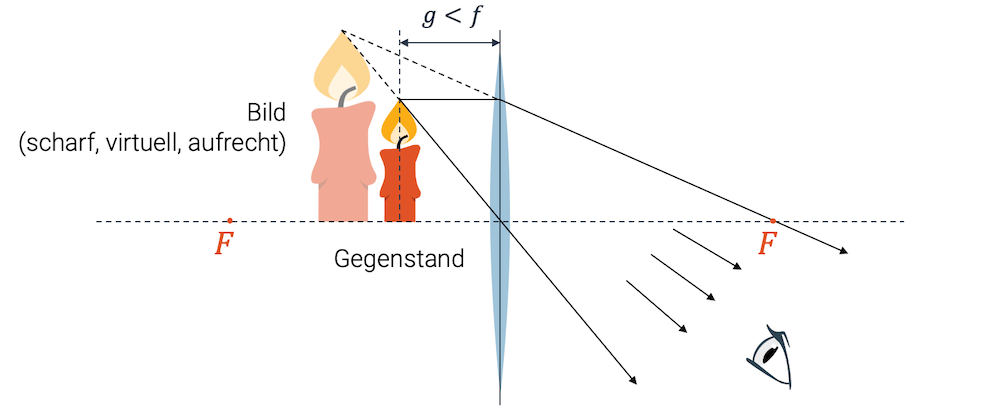
Strahlen, die nach der Linse divergieren, d.h. auseinander laufen können sich somit nicht in einem Bildpunkt treffen. Wir können keinen reellen Bildpunkt konstruieren.

Ein Betrachter (nach der Linse) könnte diese beiden Lichtstrahlen sehen und würde annehmen, dass sie gerade, d.h. ungebrochen verlaufen. Der Beobachter nimmt also an, dass die Strahlen von ihrer gestrichelt gezogenen Verlängerung her kommen.

Die beiden Verlängerungen der Lichtstrahlen treffen sich vor der Linse (links) in einem virtuellen Bildpunkt, d.h. der Beobachter hat das Gefühl, Lichtstrahlen zu sehen, die von der virtuellen Flammenspitze kommen.

Das Bild ist virtuell, da die beiden Lichtstrahl im Bildpunkt nicht physisch vorkommen. Der Betrachter meint nur, sie kämen aus diesem gemeinsamen Punkt. Tatsächlich entstammen sie aber von der Spitze des Gegenstands, die aber an einem anderen Ort ist.

Die Situation (\(g < f \)), die wir oben abgebildet haben, entspricht der Verwendung einer Lupe 🔍. Das Bild ist vergrössert und steht aufrecht.

Wenn du eine Lupe verwendest, hältst du die Lupe so nahe an den Gegenstand heran, dass er zwischen Brennpunkt und Linsenebene zu liegen kommt. Mit der gleichen Lupe in die Ferne schauend, siehst du die Welt auf dem Kopf, da wir dann eine Gegenstandsweite haben, die wieder grösser ist als die Brennweite und wir wieder ein reelles, umgekehrtes Bild erhalten der Landschaft haben.

Es ist eine besondere Eigenschaft der Sammellinsen, je nach Gegenstandsweite \(g\) zwischen umgekehrtem und aufrechtem Bild zu wechseln. Beobachtet man gerade das “Umkippen” des Bilds, handelt es sich um den Grenzfall \(g=f\), bei welchem kein Bild möglich ist. Der Abstand im Kipppunkt verrät natürlich auch gleich die Brennweite der Linse.

Streulinsen sind deshalb etwas langweiliger als Sammellinsen. Streulinsen kennen kein “Umkippen” und können nur virtuelle Bilder erzeugen.

Verschiedene Bilder bei Sammellinsen: Übersicht

In der nachfolgenden Grafik sind die verschiedenen Kombinationen eines Gegenstand und einer Sammellinse zusammengefasst:

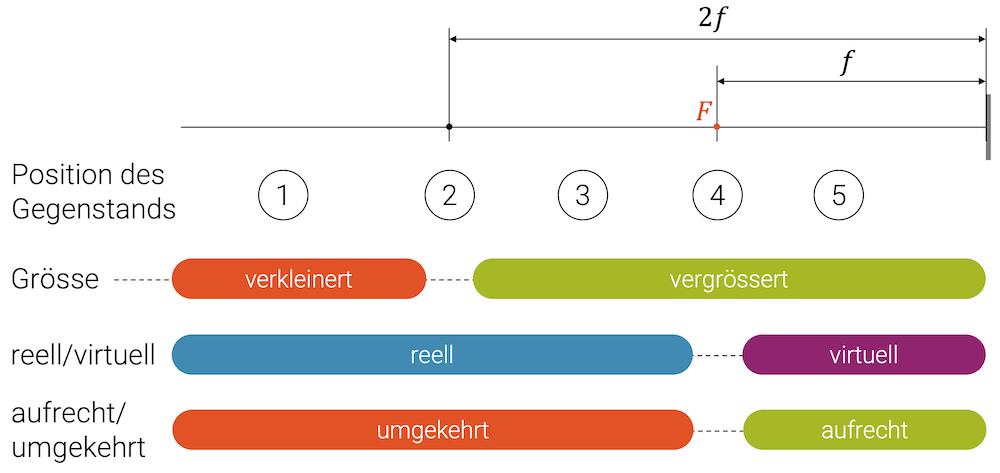
Ist der Gegenstand weiter als die Brennweite von der Linse entfernt (\(g>f\)), haben wir sicher ein reelles umgekehrtes Bild. Am Anfang ist es noch vergrössert, wird dann aber immer kleiner.

Nahe an der Linse haben wir die Situation der Lupe mit einem aufrechten, virtuellen Bild.

Linsengleichung

Mit der Linsengleichung werden Gegenstandsweite \(g\), Brennweite \(f\) und Bildweite \(b\) miteinander verknüpft. Wir können mit ihr berechnen, wo das reelle Bild hinter der Linse mit Brennweite \(f\) entsteht, wenn der Gegenstand in einem bestimmten Abstand \(g\) vor der Linse steht.

\[ \frac{1}{f} = \frac{1}{g} + \frac{1}{b} \]

Die Linsengleichung funktioniert auch für virtuelle Bilder, wobei die virtuellen Grössen ein negatives Vorzeichen bekommen.

Beispiel

Eine \(10\,\mathrm{cm}\) hohe Kerze steht im Abstand \(g=20\,\mathrm{cm}\) vor einer Sammellinse mit Brennweite \(f=8\,\mathrm{cm}\). Wo müssen wir ein weisses Blatt Papier hinter der Linse hinhalten, um das scharfe Bild zu sehen? Wie gross ist das Bild?  

Lösung

Mit der Linsengleichung erhalten wir: \[ \frac{1}{b} \;\;=\;\; \frac{1}{f} \;-\; \frac{1}{g} \;\;=\;\; \frac{1}{0.08\,\mathrm{m}} \;-\; \frac{1}{0.2\,\mathrm{m}} \] \[ = 12.5\,\mathrm{m^{-1}} – 5\,\mathrm{m^{-1}} \;\;=\;\; 7.5\,\mathrm{m^{-1}} \] Nun bilden wir den Kehrwert von \(\frac{1}{b}\) und erhalten: \[ b = \frac{1}{7.5\,\mathrm{m^{-1}}} = 0.133\,\mathrm{m} = 13.3\,\mathrm{cm} \] Um die Grösse des Bildes \(B\) zu berechnen, benutzen wir den Scheitelpunktstrahl und wenden den Strahlensatz an. Die Kerze erzeugt ein rechtwinkliges Dreieck mit der Höhe \(G=10\,\mathrm{m}\). Rechts erzeugt das Bild ein ähnliches Dreieck mit der Höhe \(B\). Der Strahlensatz besagt, dass die Seitenlängen in ähnlichen Dreiecken zueinander proportional sind. Wir können deshalb schreiben: \[ \frac{G}{g} = \frac{B}{b} \] Wir lösen nach der unbekannten Bildhöhe \(B\) auf und setzen die Werte ein: \[ B = \frac{b}{g} \cdot G = \frac{0.133\,\mathrm{m}}{0.2\,\mathrm{m}} \cdot 10\,\mathrm{cm} = \underline{6.65 \,\mathrm{cm}} \]

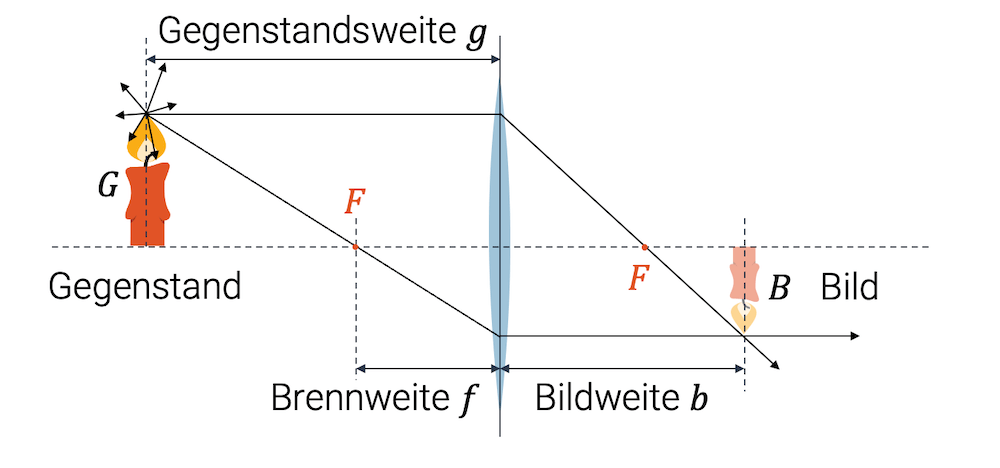
Herleitung der Linsengleichung

Wenn wir den Scheitelpunktstrahl einzeichnen, erhalten wir zwei ähnliche, rechtwinklige Dreiecke. Aus der Ähnlichkeit folgt, dass die Längenverhältnisse gleich sind und wir den Strahlensatz anwenden können:

\[ \frac{G}{g} = \frac{B}{b} \quad \mathrm{bzw.} \quad \frac{B}{G} = \frac{b}{g} \]

Wir behalten die Gleichung für den Moment und werden sie erst später wieder hervor nehmen. 🧐

Nun betrachten wir den Brennpunktstrahl nach der Linse. Die beiden markierten rechtwinkligen Dreiecke haben die gleichen Winkel und sind dadurch auch geometrisch ähnlich, d.h. ihre Seitenlängen stehen im gleichen Verhältnis:

Im linken Dreieck ist das Verhältnis der vertikalen Kathete zur horizontalen Kathete: \(G\) zu \(f\).

Im rechten Dreieck ist das Verhältnis der vertikalen Kathete zur horizontalen Kathete: \(B\) zu \((b-f)\).

Weil die Verhältnisse gleich sind, können wir sie in eine Gleichung setzen:

\[ \frac{G}{f} = \frac{B}{(b-f)} \]

Wir dividieren durch \(B\) und multiplizieren mit \(f\):

\[ \frac{G}{B} = \frac{f}{b-f} \]

Nun bilden wir den Kehrwert der Gleichung:

\[ \frac{B}{G} = \frac{b-f}{f} \]

\[ \frac{B}{G} = \frac{b}{f} \;-\; 1 \]

Links setzen wir die erste Gleichung, die wir aus dem Strahlensatz erhalten haben für den Ausdruck \(\frac{B}{G}\) ein und erhalten:

\[ \frac{b}{g} = \frac{b}{f} \;-\; 1 \]

Division durch \(b\) führt zu:

\[ \frac{1}{g} = \frac{1}{f} \;-\; \frac{1}{b} \quad \mathrm{bzw.} \quad \frac{1}{f} = \frac{1}{b} + \frac{1}{g} \]

Damit erhalten wir diese elegante Linsengleichung.

Simulation

Mit der folgenden Simulation kannst du die Entstehung von reellen und virtuellen Bildern und die ganze Strahlenkonstruktion sehr einfach nachvollziehen. Es lohnt sich ein bisschen damit herum zu spielen, um ein Gefühl für die richtigen Strahlenläufe zu entwickeln.

Bewege die Spitze des Gegenstands Object mit der Maus. Der Brennpunkt wird verändert, indem du das Label Focus‘ verschiebst.

• Simulation der Strahlenverläufe durch eine Sammel- bzw. Streulinse