Beschleunigungsarbeit

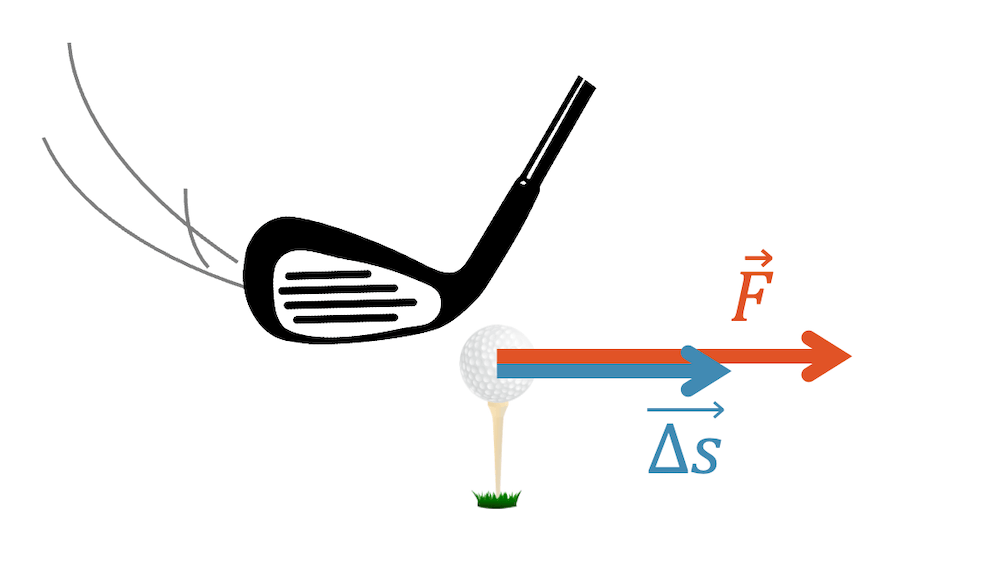
Beschleunigung und Bremsen

Newtons Zweites Gesetz \(F=m \cdot a\) besagt, dass eine Kraft \(F\) eine Masse \(m\) mit der Beschleunigung \(a\) beschleunigt. Anders herum können wir eine Beschleunigung einer Masse nur mit Hilfe einer Kraft erreichen. Für die Beschleunigung, z.B. wenn wir mit dem Fahrrad schneller werden möchten, oder wenn das Auto beschleunigen möchte, braucht es eine Antriebskraft.

Für das Bremsen gilt genau das Gleiche. Um langsamer zu werden, was einer negativen Beschleunigung entspricht, braucht es eine bremsende Kraft, die entgegen der Wegrichtung gerichtet ist. In den meisten Fällen ist die bremsende Kraft eine Reibungskraft, d.h. hier dürfte man auch von (negativer) Reibungsarbeit sprechen.

Ausser der Kraft, braucht es zusätzlich einen gewissen Weg \(\Delta s\), über welchen die Kraft wirksam ist.

Wenn wir eine wirkende Kraft haben und diese Kraft über einen gewissen Weg wirkt, wird Beschleunigungsarbeit \(W\) verrichtet. Die Geschwindigkeit geht von \(v_1\) auf \(v_2\) hoch (\(W\) positiv) oder bei einer bremsenden Kraft von \(v_1\) auf \(v_2\) herunter (\(W\) negativ).

\[ W \;\;=\;\; \frac{1}{2} m v_2^2 \;-\; \frac{1}{2} m v_1^2 \]

Bei der positiven Beschleunigungsarbeit \(W\) erhält das beschleunigte System zusätzliche kinetische Energie und wird immer schneller. Ist die Beschleunigungsarbeit \(W\) negativ, gibt das System Energie ab.

\[ W \;\;=\;\; E_{\text{kin},2} \;-\; E_{\text{kin},1} \]

Zentripetalbeschleunigung: Änderung der Richtung ohne Arbeit

Es gibt auch Fälle, in welchen eine Kraft über einen Weg wirkt, ohne dass die Masse schneller oder langsamer wird. Wenn die Kraft und der Weg senkrecht zu einander stehen, ändert die Kraft nur die Richtung der Geschwindigkeit, nicht deren Betrag.

Das ist der Fall bei der sog. Zentripetalbeschleunigung, die zum Zentrum der Kurve oder der Kreisbahn zeigt. 🧐

Ohne Änderung des Betrags der Geschwindigkeit, ändert sich energetisch nichts. Die Masse wird durch die Zentripetalbeschleunigung nur umgelenkt, jedoch ist die Bewegung dadurch weder beschleunigt, noch abgebremst.

Es gibt v.a. zwei Beispiele:

• Gravitationskraft auf einen Himmelskörper, der sich auf einer Kreisbahn bewegt
• Lorentzkraft auf eine elektrische Ladung

Wenn wir die Umlaufbahn der Erde als Kreis betrachten (was näherungsweise stimmt) ist die Gravitationskraft der Sonne genau senkrecht zur Bewegung. Damit kann die Sonne über diese Kraft keine Beschleunigungsarbeit verrichten: Die Erde behält eine konstante Geschwindigkeit.

Im Fall des Kometen ist die Bahn aber stark elliptisch, so dass die Parallelkomponente, parallel zur Bewegung, eine Beschleunigungsarbeit bewirkt. Bei der Annährung zur Sonne bedeutet das eine Beschleunigung: Der Komet erreicht sehr hohe Geschwindigkeiten. Beim sich Entfernen bedeutet das ein Abbremsen.

Die Lorentzkraft eines Magnetfelds wirkt immer senkrecht zur Geschwindigkeit der elektrischen Ladung. Das hat damit zu tun, dass sie aus einem Vektorprodukt berechnet wird und dass das Vektorprodukt immer senkrecht auf den ursprünglichen Vektoren steht.

Die Lorentzkraft eines Magnetfelds ist:

\[ \vec{F} = q \cdot \big( \vec{v} \times \vec{B} \big) \]

Die Lorentzkraft wird deshalb nie in der Lage sein, Beschleunigungsarbeit zu verrichten, denn es gilt immer \( \vec{F} \perp \vec{v} \). Die Lorenzkraft lenkt die Ladung nur ab.

Herleitung der Beschleunigungsarbeit Formel

Wir starten mit dem allgemeinen Ausdruck für die Arbeit:

\[ W = F \cdot \Delta s \]

Nun setzen wir für \(F\) das Newton’sche Zweite Gesetz \(\;F=m \cdot a\;\) ein:

\[ W = (ma) \cdot \Delta s = m \cdot (a \Delta s) \]

Für die Beschleunigung \(a\) können wir die folgende Bewegungsgleichung einsetzen:

\[ v_2^2 = v_1^2 + 2 a \Delta s \]

Wir lösen nach \(a \Delta s\) auf und setzen ein

\[ a \Delta s = \frac{1}{2} (v_2^2 – v_1^2) \]

\[ W = m \cdot \frac{1}{2} (v_2^2 – v_1^2) \]

Damit erhalten wir den Ausdruck für die Beschleunigungsarbeit, die verrichtet werden muss, um eine Masse \(m\) von \(v_1\) auf \(v_2\) zu beschleunigen: 🙂

\[ W \;\;=\;\; \frac{1}{2} m v_2^2 \;-\; \frac{1}{2} m v_1^2 \]

Mit der Definition der kinetischen Energie \(\;E_{\text{kin}} = \frac{1}{2} m v^2 \;\) erhalten wir:

\[ W \;\;=\;\; E_{\text{kin},2} \;-\; E_{\text{kin},1} \]