Inhalt
Das Wichtigste in Kürze
Die Winkelgeschwindigkeit \(\omega\) wird manchmal auch Kreisfrequenz genannt. Sie beschreibt, wie schnell sich ein Winkel (z.B. bei einer Kreisbewegung) mit der Zeit ändert. Die Winkelgeschwindigkeit wird in der Physik oft auch bei der Beschreibung von Schwingungen oder Wellen verwendet.
Abkürzung: \(\omega\) (kleines Omega)
Einheit: \(\text{s}^{-1}\;\;\), seltener auch: \(\;\;\text{Hz}\;\;\) (Hertz)
Die Winkelgeschwindigkeit ist verwandt mit der Frequenz \(f\), die um den Faktor \(2\pi\) kleiner ist, da sie die ganze Umdrehung als 1 zählt, während die Winkelgeschwindigkeit die ganze Umdrehung als \(2\pi\) (Bogenmass für 360°) benutzt:
\[ \omega = 2\pi \cdot f \]
Videos
Häufigste Fragen
Die Winkelgeschwindigkeit ist ein Unterthema der Kreisbewegung. Du findest dort zusätzliche Infos.
Eine Kreisbewegung wird vorzugsweise mit der Winkelgeschwindigkeit \(\omega\) (kleines Omega) beschrieben.
Sie hat den Vorteil, dass sie für den ganzen rotierenden Körper immer gleich gross ist, unabhängig vom betrachteten Punkt.
Die Winkelgeschwindigkeit beschreibt, wie schnell sich der Winkel bei der Kreisbewegung ändert. Eine ganze Umdrehung entspricht einer Änderung des Winkels um \(2\pi\) (eine ganze Umdrehung im Bogenmass).
Im Unterricht benutze ich gerne einen Tennisball, der an einer Schnur befestig ist.
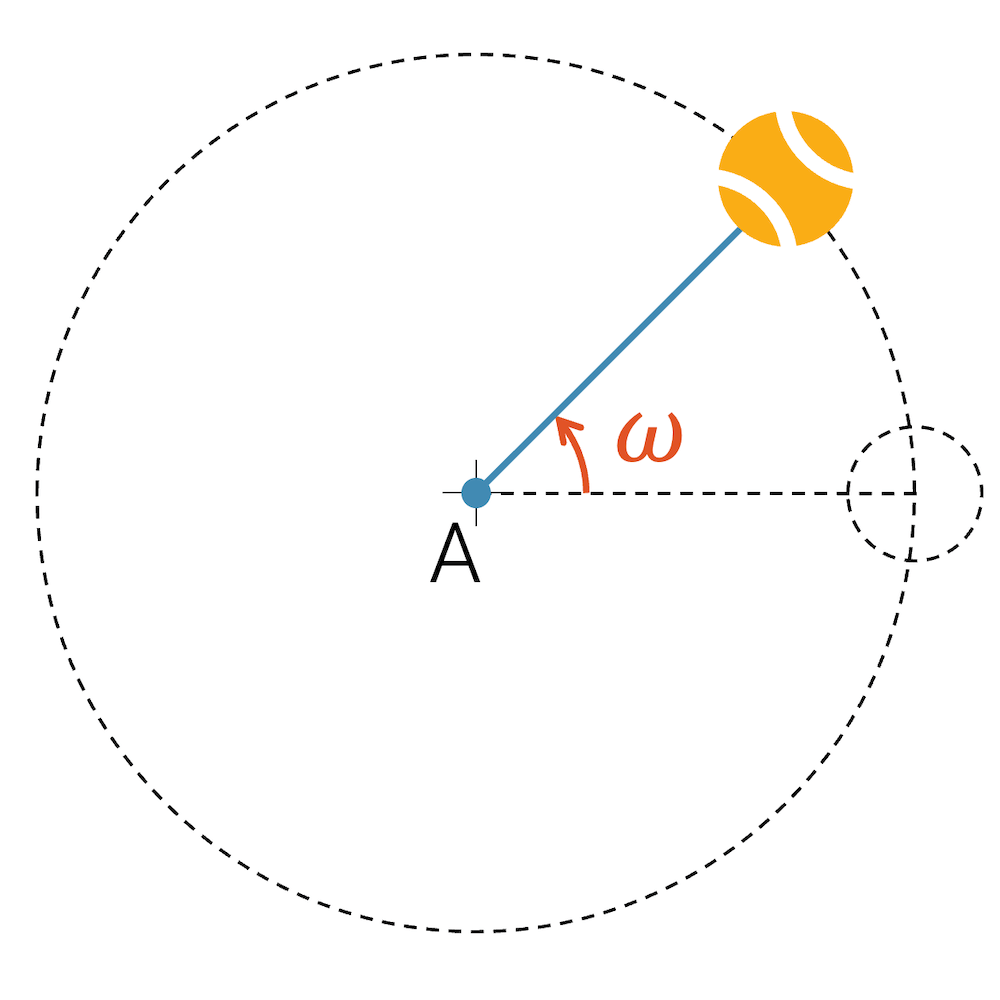
Wenn ich den Ball einmal pro Sekunde kreisen lasse, hat er eine Winkelgeschwindigkeit von \(\omega = 2\pi\;\text{s}^{-1}\).
Ein viel langsamerer Sekundenzeiger braucht genau eine Minute, um den Winkel von \(2\pi\) zurückzulegen. Seine Winkelgeschwindigkeit beträgt deshalb:
\[ \omega = \frac{2\pi}{1\,\text{min}} = \frac{2\pi}{60\,\text{s}} = \frac{\pi}{30}\;\text{s}^{-1} \]
Beachte, dass die Einheit der Winkelgeschwindigkeit “Radian pro Sekunde” ist. “Radian” steht für Bogenmass ist im Grunde genommen einfach eine Zahl (ohne Einheit). Wir schreiben deshalb kurz “pro Sekunde”:
\[ [\omega] = \text{s}^{-1} \]
Beispiel: Berechnung der Winkelgeschwindigkeit
Wie viel beträgt die Winkelgeschwindigkeit des Minutenzeigers einer Uhr?
Winkelgeschwindigkeit und Bahngeschwindigkeit
Zwei Zahnräder, die sich berühren, drehen sich unterschiedlich schnell, wenn sie verschieden gross sind.
Das damit zu tun, dass der kurzzeitige Berührungspunkt auf beiden Zahnrädern mit der gleichen Bahngeschwindigkeit unterwegs ist.
Das muss er auch, denn sonst würden sich die Zahnräder in diesem Punkt nicht nur berühren, sondern sie würden aneinander reiben, was zu unnötigen Reibungsverlusten führen würde (Materialverschleiss, Erwärmung etc).
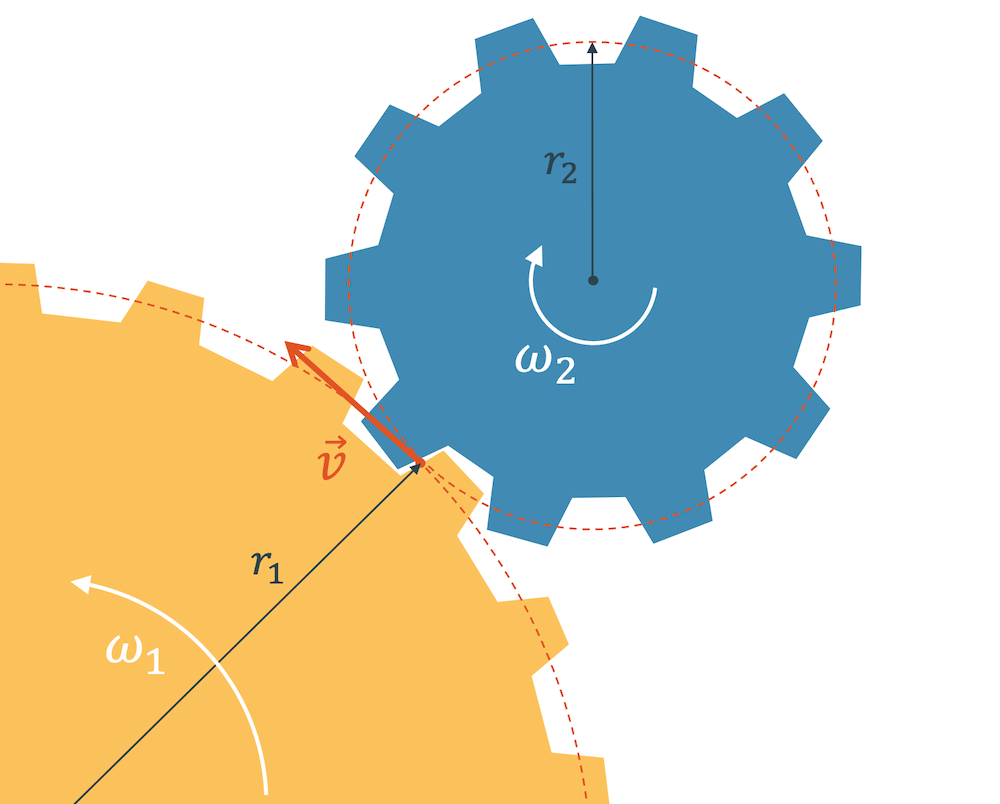
Wenn wir die Formel für die Berechnung der Bahngeschwindigkeit zur Hand nehmen, dann erhalten wir für das Zahnrad 1:
\[ v = r_1 \cdot \omega_1 \]
Für das Zahnrad 2:
\[ v = r_2 \cdot \omega_2 \]
Jetzt setzen wir die beiden Bahngeschwindigkeiten \(v\) gleich und erhalten die Gleichung:
\[ r_2 \cdot \omega_2 = r_1 \cdot \omega_1 \]
Wir dividieren durch r_2 und erhalten schliesslich:
\[ \omega_2 = \frac{r_1}{r_2} \cdot \omega_1 \]
Das Zahnrad 2 dreht sich mit einer Winkelgeschwindigkeit \(\omega_1\), die um den Faktor \(r_1/r_2\) grösser ist, als beim Zahnrad 1. Wenn beispielsweise das Zahnrad 2 einen halb so grossen Durchmesser bzw. Radius hat als das Zahnrad 1, dann dreht es sich doppelt so schnell.
Das ist logisch, denn wenn der Umfang des kleineren Zahnrad halb so gross ist, dann muss das kleine Zahnrad zwei mal drehen, bis der gleiche Berührungspunkt auf dem grossen Zahnrad einen ganzen Umfang geschafft hat.
Beispiel: Zwei Zahnräder
Mit welcher Winkelgeschwindigkeit dreht sich ein kleines Zahnrad (20 Zähne), wenn das ihn berührende grosse Zahnrad (80 Zähne) genau 1’200 Umdrehungen pro Minute macht?
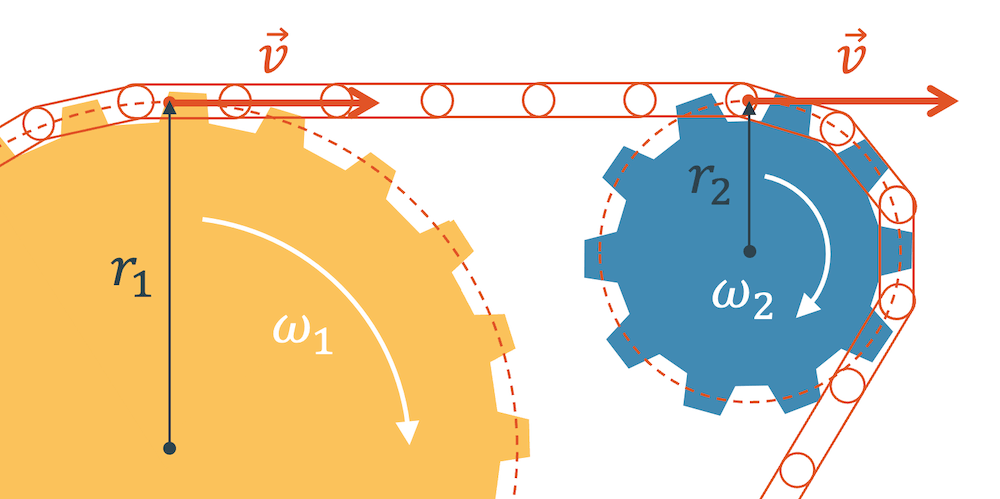
Bei einem Kettenantrieb ist die Überlegung genau gleich. Die Kette hat immer die gleiche Geschwindigkeit \(v\), die der Bahngeschwindigkeit beim grossen, wie auch beim kleinen Zahnrad entspricht.
Wir setzen wieder beide Bahngeschwindigkeiten gleich und erhalten die gleiche Gleichung. Der einzige Unterschied ist die Drehrichtung: Beide Zahnräder drehen jetzt in die gleiche Richtung.
Aufgabensammlung
Lernziele
- Du kannst die Winkelgeschwindigkeit berechnen und mit korrekter Einheit angeben.
Weitere Links
Winkelgeschwindigkeit (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.