Inhalt
Das Wichtigste in Kürze
Bei Kreisbewegungen ist die Bahngeschwindigkeit \(v\) die Geschwindigkeit eines Punktes auf einer Kreisbahn mit Radius \(r\). Die Richtung der Bahngeschwindigkeit ist tangential zum Kreis der Kreisbewegung.
\[ v = r \cdot \omega \]
Dabei ist \(\omega\) die Winkelgeschwindigkeit der Kreisbewegung.
Einheit der Bahngeschwindigkeit:
\[ [\;v\;] = \frac{\text{m}}{\text{s}} \]
Je grösser der Abstand \(r\) vom Drehzentrum, desto grösser ist die Bahngeschwindigkeit. Deshalb haben beim Propeller die Enden die grösste Bahngeschwindigkeit, während das Drehzentrum selbst die Bahngeschwindigkeit null hat.
Wir können die Bahngeschwindigkeit auch mit Hilfe des Kreisumfangs \(U\) und der Periode \(T\) berechnen, die für eine Umrundung benötigt wird:
\[ v = \frac{U}{T} = \frac{2 \pi r}{T} \]
Videos
Häufigste Fragen
Die Bahngeschwindigkeit ist ein Unterthema der Kreisbewegung. Du findest dort zusätzliche Infos.
Richtung der Bahngeschwindigkeit
Bei einer Kreisbewegung wandern Teile eines sich drehenden Körpers auf Kreisbahnen. Wie schnell diese unterwegs sind, wird durch die Bahngeschwindigkeit beschrieben.
Die Richtung der Bahngeschwindigkeit ist immer tangential zum Kreis.
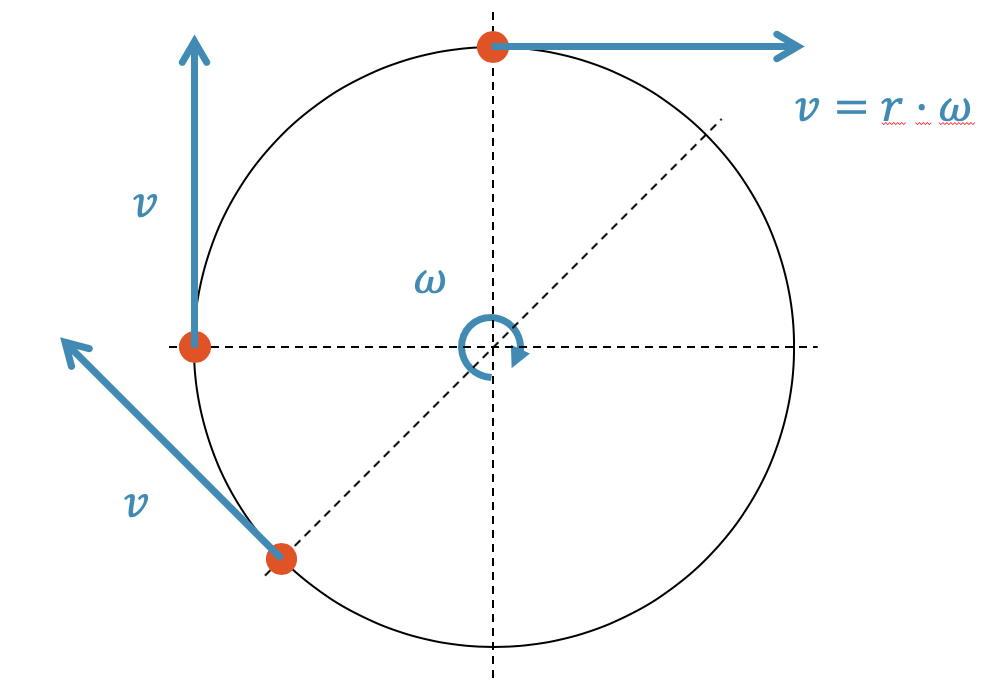
Wir sehen das auch sehr schön in folgendem Beispiel:
Beispiel: Trennscheibe
Eine Trennscheibe dreht mit sehr grosser Winkelgeschwindigkeit und bringt das bearbeitete Metall zum Glühen. Erkläre die Richtung der Leuchtspuren auf dem Bild und vergleiche sie mit der Kreisbewegung und der Bahngeschwindigkeit.

“Zwei Punkte können unterschiedliche Bahngeschwindigkeiten haben, obwohl sie zum gleichen Körper gehören, der die eine Winkelgeschwindigkeit, Frequenz oder Periode hat.”
Betrag der Bahngeschwindigkeit
Die Drehgeschwindigkeit von Kreisbewegungen kann mit verschiedenen Grössen beschrieben werden: Die Winkelgeschwindigkeit, die Frequenz oder die Periode sind Grössen, die z.B. für den ganzen Sekundenzeiger gelten, egal, ob wir etwa von seiner Spitze oder seiner Drehachse sprechen.
Bei der Bahngeschwindigkeit ist das anders: Die Spitze des Sekundenzeigers hat die höchste Bahngeschwindigkeit. Die Achse des Sekundenzeigers hat hingegen eine Bahngeschwindigkeit, die null ist.
Nehmen wir das Beispiel des Tennisball, der an einer Schnur befestigt ist:
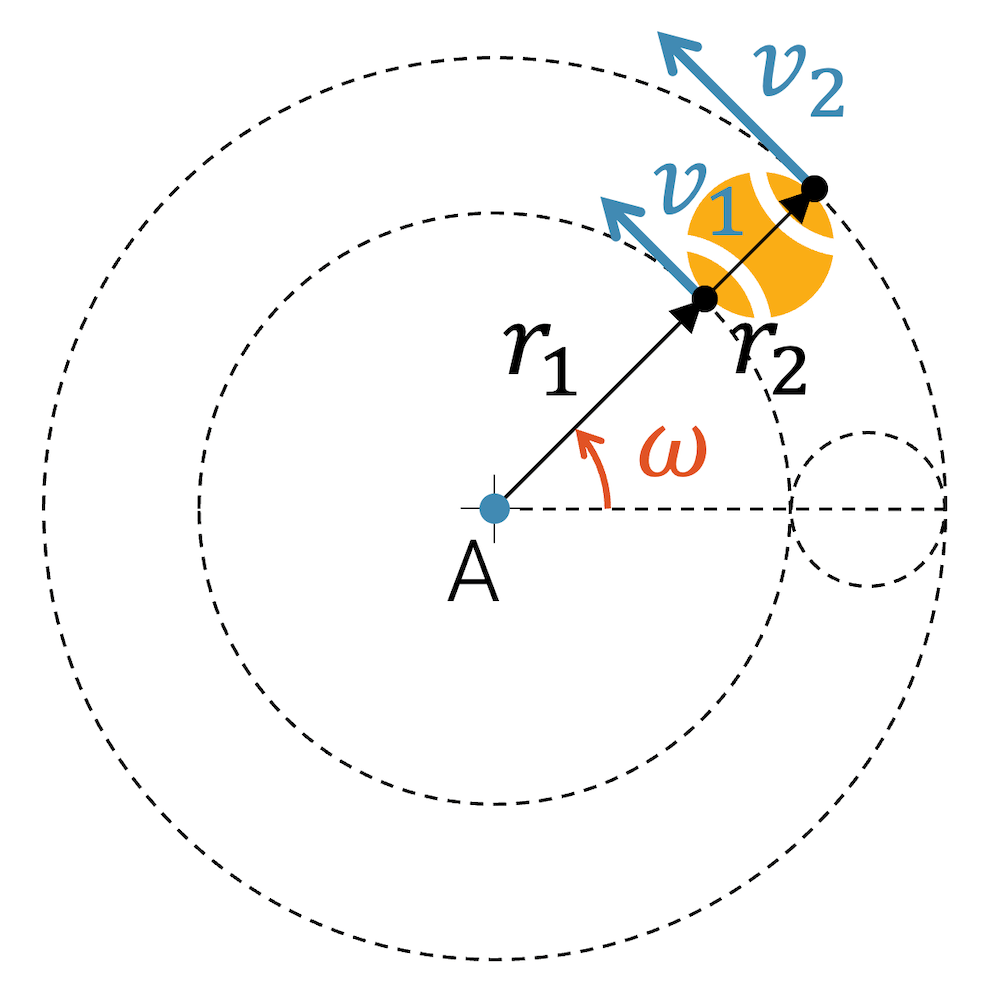
Wenn wir die Bahngeschwindigkeit der beiden Punkte Innenbahn 1 und Aussenbahn 2 vergleichen, so sehen wir, dass der Punkt auf der Aussenbahn einen grösseren Kreis zurücklegt. Er schafft den grösseren Umfang in der gleichen Zeit, wie der Punkt auf der Innenbahn, d.h. er muss deshalb schneller unterwegs sein.
Bei einem Propeller dreht sich der Punkt an der Drehachse um sich selbst. Er hat keine Bahngeschwindigkeit und wir könnten ihn theoretisch mit dem Finger berühren. Das Ende eines Propellerrotors ist dagegen sehr schnell unterwegs und hat eine grosse Bahngeschwindigkeit.
Für die Bahngeschwindigkeit können wir einfach die Frage stellen: Wie gross ist die Strecke \(\Delta s\) z.B. für einen Umfang und wie gross ist die Periode \(T\), die für einen ganzen Umfang \(U=2\pi r\) nötig war:
\[ v = \frac{\Delta s}{\Delta t} = \frac{2\pi r}{T} \]
Die Winkelgeschwindigkeit ist ähnlich: Sie sagt, wie viel Winkel die Kreisbewegung macht pro Zeit. Für eine ganze Umdrehung nimmt sie nicht den Umfang, sondern den Winkel von \(2\pi\) im Bogenmass (oder eben den Bogen des Einheitskreises):
\[ \omega = \frac{2\pi}{\Delta t} \]
Wir können diesen Ausdruck nach \(2\pi\) umformen
\[ 2\pi = \omega \cdot \Delta t \]
und oben im Ausdruck für die Bahngeschwindigkeit einsetzen. Wir erhalten dann:
\[ \require{cancel} v = \frac{2\pi \cdot r}{\Delta t} = \frac{(\omega \cdot \cancel{\Delta t}) \cdot r}{\cancel{\Delta t}} \]
\[ v = r \cdot \omega \]
Die Bahngeschwindigkeit \(v\) ist abhängig vom Abstand \(r\) zum Drehzentrum. Sie nimmt linear mit dem Abstand (Radius) zu: Je grösser der Abstand, desto grösser der Umfang, desto grösser die Bahngeschwindigkeit.
Für das Drehzentrum selbst ist der Abstand null und die Bahngeschwindigkeit dann ebenfalls null.
Beispiel: Bahngeschwindigkeit der Erde
Berechne die Bahngeschwindigkeit der Erde in km/h. Die Erdbahn kann als Kreis um die Sonne approximiert werden, mit Radius \(r=150.42 \cdot 10^6\;\text{km}\)
Beispiel: Bahn eines geostationären Satelliten
Wie gross ist die Bahngeschwindigkeit eines geostationären Satelliten, der im Abstand von 42’240 km vom Erdmittelpunkt entfernt ist?
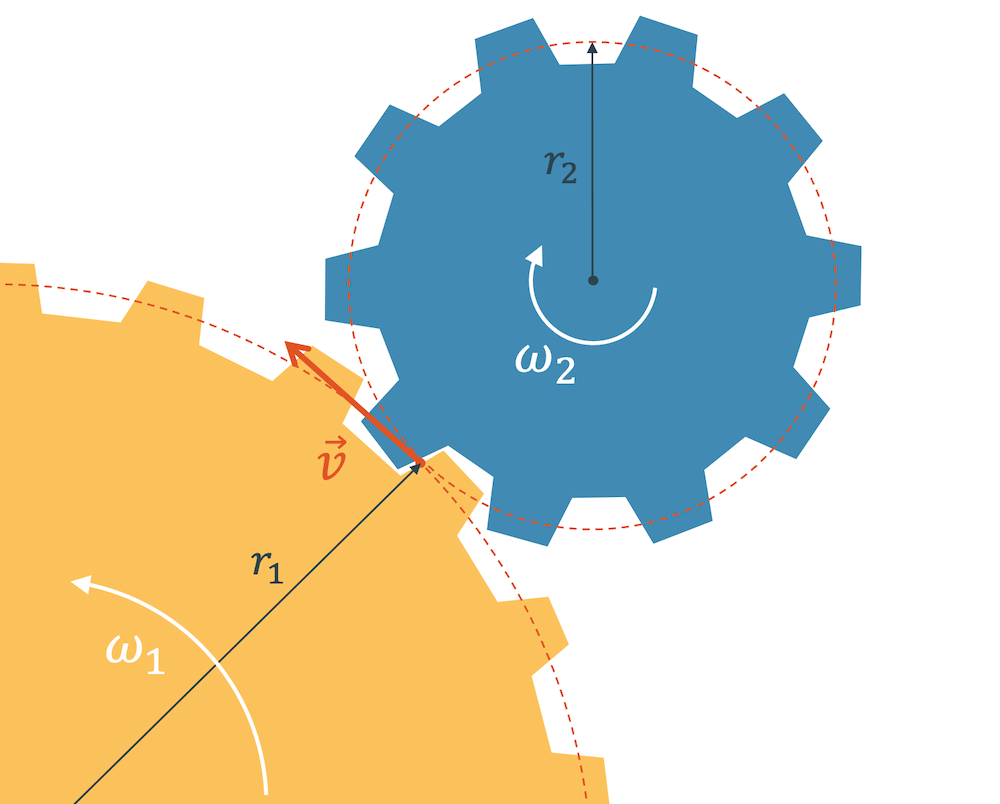
Bahngeschwindigkeit bei Zahnrädern
Zahnräder, die sich berühren, drehen sich mit unterschiedlichen Winkelgeschwindigkeiten, wenn sie verschieden gross sind. Sie berühren sich aber in einem Punkt, der für beide Zahnräder die gleiche Bahngeschwindigkeit hat.
Das muss so sein, denn sonst würden sich die Zahnräder in diesem Punkt nicht nur berühren, sondern sie würden aneinander reiben, was zu unnötigen Reibungsverlusten führen würde (Materialverschleiss, Erwärmung etc).
Das Gleiche gilt auch beim Einsatz von Ketten oder Riemen: Die Bahngeschwindigkeit \(v\) des ersten Zahnrads wird auf die Kette übertragen, die immer mit \(v\) unterwegs ist. Diese überträgt diese Geschwindigkeit auf das zweite Zahnrad, welches daraus eine Winkelgeschwindigkeit erhält.
Beachte, dass die Drehrichtung beim Kettenantrieb die Gleiche ist.
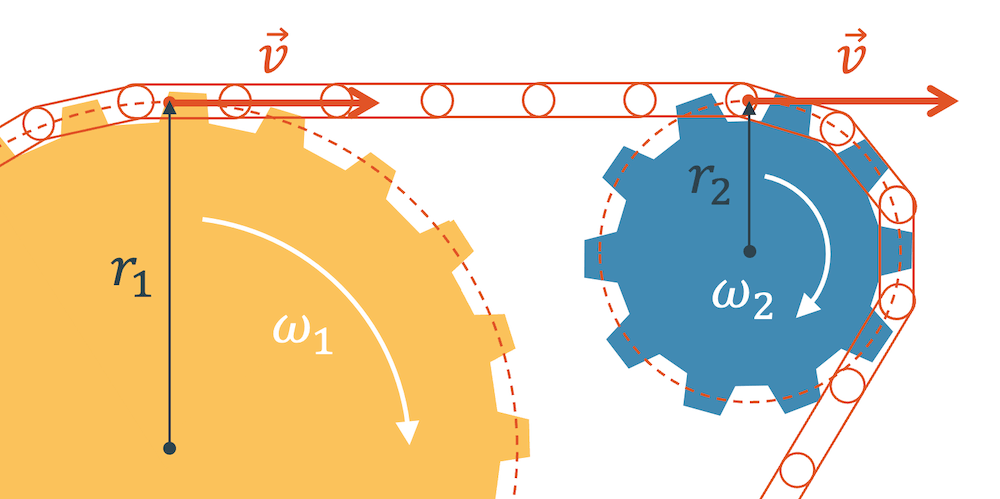
Im Artikel zur Winkelgeschwindigkeit leiten wir aus der Bedingung, dass die Bahngeschwindigkeiten beider Zahnräder gleich sein muss, eine Gleichung her und damit ein Verhältnis für die Winkelgeschwindigkeiten der beiden Zahnräder (mit Rechenbeispiel).
Aufgabensammlung
Lernziele
- Du weisst, dass bei einer Kreisbewegung eines Körpers, die Winkelgeschwindigkeit für den ganzen Körper gilt, die Bahngeschwindigkeit jedoch vom Radius des betrachteten Punkts abhängt.
- Du kannst Bahngeschwindigkeiten und Winkelgeschwindigkeiten berechnen oder sie ineinander umrechnen, jeweils mit korrekten Einheiten
Weitere Links
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.