Inhalt
Das Wichtigste in Kürze
Die Beschleunigungsarbeit ist eine Art von physikalischer Arbeit. Sie wird verrichtet, wenn eine Masse von der Geschwindigkeit \(v_1\) auf die Geschwindigkeit \(v_2\) beschleunigt wird:
\[ W = \frac{1}{2} m v_2^2 – \frac{1}{2} m v_1^2 \]
Videos
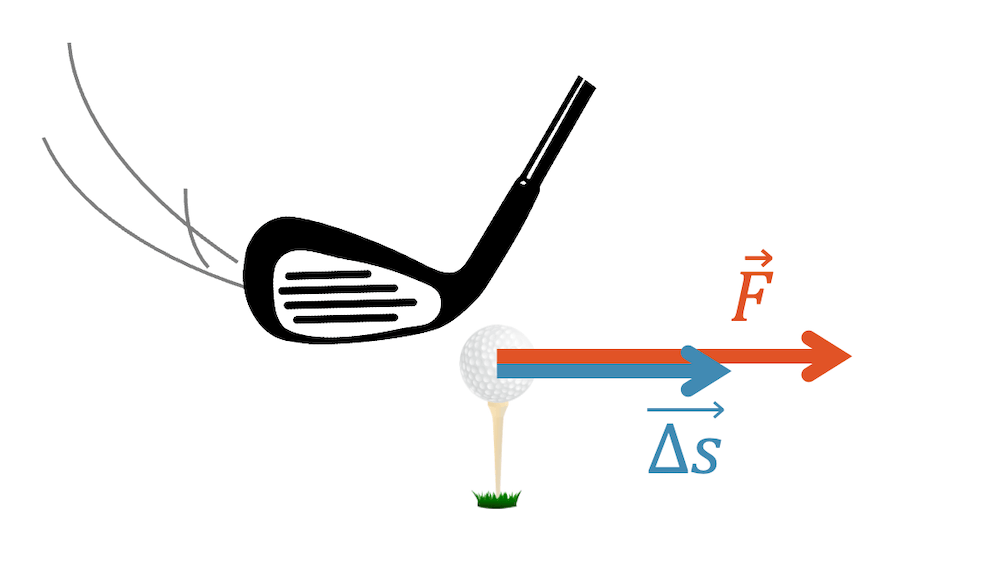
Beschleunigung und Bremsen
Wir wissen, dass Newtons Zweites Gesetz \(F=m \cdot a\) besagt, dass eine Kraft \(F\) eine Masse \(m\) beschleunigt (Beschleunigung \(a\)). Anders herum können wir eine Beschleunigung einer Masse nur mit Hilfe einer Kraft erreichen. Ausser der Kraft, braucht es zusätzlich einen gewissen Weg \(\Delta s\), über welchen die Kraft wirksam ist.
Für die Beschleunigung, z.B. wenn wir mit dem Fahrrad schneller werden möchten, oder wenn das Auto beschleunigen möchte, braucht es eine Antriebskraft.
Für das Bremsen gilt genau das Gleiche. Um langsamer zu werden, was einer negativen Beschleunigung entspricht, braucht es eine bremsende Kraft, die entgegen der Wegrichtung gerichtet ist. In den meisten Fällen ist die bremsende Kraft eine Reibungskraft, d.h. hier darf man auch von (negativer) Reibungsarbeit sprechen.
Beschleunigungsarbeit Beispiel: Golfball
Ein Golfball (\(m=45.93\,\text{g}\)) wird durch einen Schlag auf eine Geschwindigkeit von 300 km/h gebracht.
Wie viel beträgt die Beschleunigungsarbeit?
Änderung der Richtung
Es gibt auch Fälle, in welchen eine Kraft über einen Weg wirkt, ohne dass die Masse schneller oder langsamer wird. Wenn die Kraft und der Weg senkrecht zu einander stehen, ändert die Kraft nur die Richtung der Geschwindigkeit, nicht deren Betrag.
Ohne Änderung des Betrags der Geschwindigkeit, ändert sich energetisch nichts. Die Masse wird durch die Kraft nur umgelenkt, jedoch weder beschleunigt, noch abgebremst.
Solche Kräfte sind Zentripetalkräfte bei einer Kreisbewegung.
Die Lorentzkraft wirkt immer senkrecht zur Geschwindigkeit der elektrischen Ladung, so dass sie nicht in der Lage ist, Beschleunigungsarbeit zu verrichtet. Sie lenkt die Ladung nur ab.
Herleitung der Beschleunigungsarbeit Formel
Wir starten mit dem allgemeinen Ausdruck für die Arbeit:
\[ W = F \cdot \Delta s \]
Nun setzen wir für \(F\) das Newton’sche Zweite Gesetz \(F=m \cdot a\) ein:
\[ W = (ma) \cdot \Delta s = m \cdot a \Delta s \]
Für die Beschleunigung \(a\) können wir die folgende Bewegungsgleichung einsetzen:
\[ v_2^2 = v_1^2 + 2 a \Delta s \]
Wir lösen nach \(a \Delta s\) auf und setzen ein
\[ a \Delta s = \frac{1}{2} (v_2^2 – v_1^2) \]
\[ W = m \cdot \frac{1}{2} (v_2^2 – v_1^2) \]
Damit erhalten wir den Ausdruck für die Beschleunigungsarbeit, die verrichtet werden muss, um eine Masse \(m\) von \(v_1\) auf \(v_2\) zu beschleunigen:
\[ W = \frac{1}{2} m v_2^2 – \frac{1}{2} m v_1^2 \]
Aufgabensammlung
Weitere Links
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.