Für das Verständnis von Wärmekraftmaschinen (WKM), Kältemaschinen und Wärmepumpen sind die Zustandsänderungen das A und O. Es geht hierbei um Änderungen von Temperatur, Volumen oder Druck von Gasen, wobei wir uns oft an den Gasgesetzen der idealen Gasen orientieren werden. Die folgenden Betrachtungen gelten aber nicht nur für ideale Gase, sondern auch für reale Gase, Gas-Flüssigkeitsgemische und Flüssigkeiten. Wir werden deshalb allgemeiner einfach von Fluiden reden.
Spezielle Zustandsänderungen
Eine reale Zustandsänderung ist meistens eine komplexe Angelegenheit. Wenn wir beispielsweise mit der Fahrradpumpe Luft in die Reifen pressen, dann erfährt die Luft eine Zustandsänderung, die nicht so einfach zu fassen wäre. Sie wird komprimiert, d.h. der Druck steigt sicherlich an. Gleichzeitig wird sie aber auch erwärmt, d.h. die Temperatur nimmt ebenfalls zu. Auch wenn die Luft als ideales Gas angesehen werden kann, so ist die Zustandsänderung dieser Luft nicht einfach zu berechnen, denn im Reifen ändern sich \(p\), \(T\) und \(n\) und schliesslich auch \(V\), denn wir drücken die in der Pumpe die eingeschlossene Luft zusammen und verkleinern ihr Volumen \(V\).
Unter speziellen Zustandsänderungen verstehen wir vereinfachte, ideale Fälle, die uns die Anwendung der Gasgesetze erlauben. Es sind dies:
Spezielle Zustandsänderungen
- isobare Kompression oder Expansion (konstanter Druck)
- isotherme Kompression oder Expansion (konstante Temperatur)
- isochore Erwärmung oder Abkühlung (konstantes Volumen)
- adiabatische Zustandsänderung (ohne Austausch von Wärme)
Zustandsänderungen im p,V-Diagramm
Wir können einen Zustand eines Gases mit den Zustandsgrössen \(p\), \(T\) und \(V\) beschreiben. Eine Möglichkeit dazu ist das p,V-Diagramm. Die beiden Zustandsgrössen \(p\) und \(V\) bestimmen als Koordinaten den Punkt des Zustands im p,V-Diagramm. Wie steht es mit der Temperatur? Zu einem bestimmten Wertepaar von \(p\) und \(V\) passt eine bestimmte Temperatur \(T\). Wenn das Gas ideal ist, können wir diese Temperatur mit der idealen Gasgleichung berechnen:
\[ pV = nRT \quad \rightarrow \quad T =\frac{pV}{nR} \]
Wenn es kein ideales Gas ist, weicht die Temperatur vom idealen Wert ab, ist aber auch eine Funktion von \(p\) und \(V\), auch wenn die Funktionsgleichung meistens unbekannt ist.
\[ T=T(p,V) \]
Daraus folgt, dass jedem Punkt im p,V-Diagramm auch eine bestimmte Temperatur zugeordnet werden kann. Wir können uns das wie bei einer Landkarte vorstellen: Jeder Ort im Gelände hat zwei geografische Koordinaten und eine Höhe. Im p,V-Diagramm ist es genauso. Wir schauen von oben auf eine “Landschaft”, in welcher die Punkte mit den drei Koordinaten \((p,V,T)\) definiert sind. Natürlich gilt das nur für eine bestimmte Menge des Gases, d.h. das Diagramm gilt für 1 kg oder für 1 mol des Gases.
Wenn wir nun den Zustand des Gases ändern, verschiebt sich dieser Punkt auf der “Karte” und ändert dabei meist auch seine “Höhe”. In anderen Worten: Durch eine Veränderung des Drucks und des Volumens ändert sich auch die Temperatur.
Beispiel
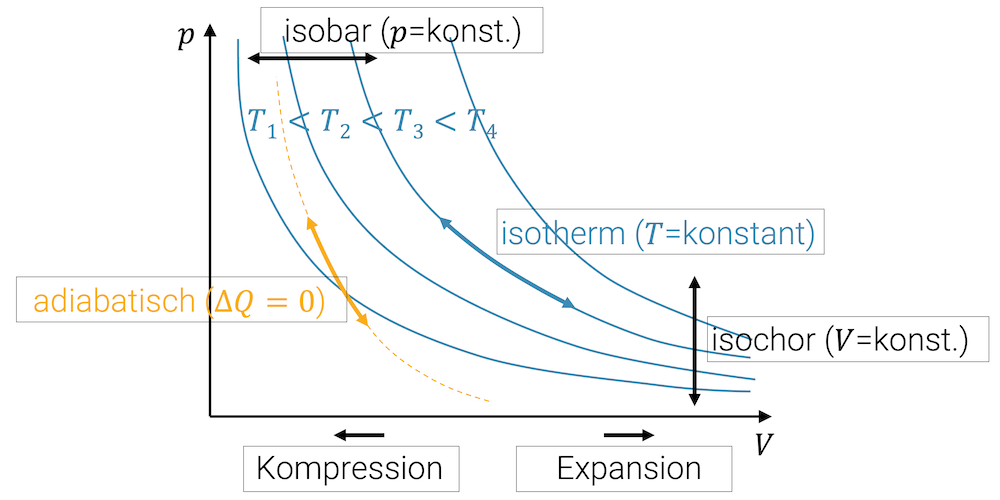
Ordne die folgenden Begriffe den im p,V-Diagramm eingezeichneten Zustandsänderungen zu:
- Kompression
- Expansion
- isobar
- isotherm
- isochor
- adiabatisch
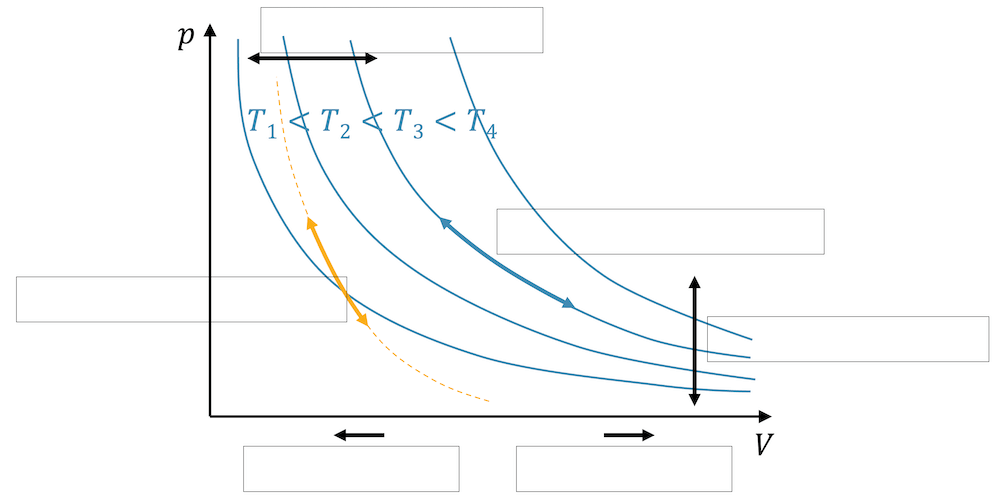
Die beiden Zustandsänderungen isobar und isochor sind sehr einfach. Ein konstanter Druck entspricht einer horizontalen Verschiebung des Punkts im Diagramm. Alle Punkte mit gleichem Volumen liegen auf einer Vertikalen im p,V-Diagramm.
Wenn das Volumen des Fluids verkleinert wird, sprechen wir natürlich von einer Kompression, d.h. einer Verschiebung nach links. Umgekehrt, ist eine Verschiebung nach rechts eine Vergrösserung des Volumens, was wir Expansion bezeichnen.
Die blauen Hyperbeln zeigen die Isothermen, d.h. die Funktionen \(p(V)\) mit konstanten Temperaturen. Zustandsänderungen, bei welchen die Temperaturen gleich bleiben, bewegen sich auf den Isothermen.
Die adiabatische Zustandsänderung ist steiler als die Isotherme, denn bei einer isothermen Kompression erhöht sich zwar der Druck, doch es wird dauernd Wärme abgeführt, damit die innere Energie nicht zunimmt. Sobald nämlich die innere Energie zunimmt, nimmt auch die Temperatur zu. Bei der adiabatischen Kompression ist die Wärmeabgabe nicht möglich, d.h. die zugeführte Arbeit führt zu einer Erhöhung der inneren Energie, so dass die Temperatur zunimmt. Der Druck nimmt natürlich auch zu, aber der Punkt bewegt sich gleichzeitig hin zu einer höher gelegenen Isothermen.
Darstellung von Arbeit im p,V-Diagramm
Wenn wir in einem Zylinder ein eingeschlossenes Fluid komprimieren, steigt der Druck. Allerdings komprimieren wir nur infinitesimal, d.h. unendlich wenig. Wenn wir das tun, dann steigt der Druck unwesentlich wenig an und wir können näherungsweise einen konstanten Druck \(p\) annehmen.
Die infinitesimale Arbeit \(\Delta W_i\), die für die infinitesimale Kompression nötig ist, berechnet sich als Produkt von Kraft \(F\) und Weg \(\Delta s\):
\[ \Delta W_i = F \cdot \Delta s \]
Die Kraft entspricht dem Produkt von Fläche und Druck: \(F=p \cdot A\)
\[ \Delta W_i = (p \cdot A) \cdot \Delta s \]
Das Produkt \(A \cdot \Delta s\) entspricht dem kleinen Volumen \(\Delta V\) um welches das Fluid komprimiert worden ist.
\[ \Delta V = A \Delta s \quad \rightarrow \quad \Delta W_i = p \cdot \Delta V \]
Somit haben wir für die Kompressionsarbeit eine Fläche im p,V-Diagramm:
\[ \Delta W_i = p \cdot \Delta V \]
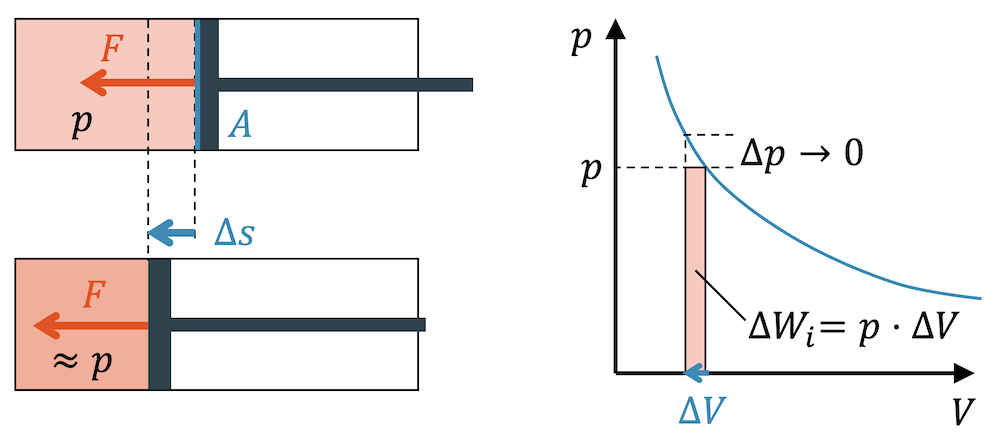
Im p,V-Diagramm entsprich \(p \cdot \Delta V\) einer Rechteckfläche. Da die Strecke \(\Delta s\) infinitesimal klein ist, ist auch \(\Delta V\) infinitesimal klein. Das Rechteck hat die volle Höhe \(p\), aber ist unendlich schmal. Diese unendlich kleine Fläche entspricht der infinitesimal kleinen Arbeit \(\Delta W_i\).
Wenn wir vom Zustand 1 zum Zustand 2 isotherm komprimieren, bewegt sich der Punkt entlang der Isothermen. Addieren wir unendlich viele Rechtecke auf dem Weg von 1 nach 2, erhalten wir die Fläche unterhalb der Kurve der Zustandsänderung. Sie entspricht der Summe aller kleinen Arbeitsbeiträge, d.h. die Arbeit, die für die Kompression des Fluids nötig ist.
\[ W_{in} = \sum_i \Delta W_i \]
Eine solche unendliche Summe von infinitesimal schmalen Rechtecken heisst Integral und wird mit einem schlanken, grossen “S” für “Summe” geschrieben. Statt einem \(\Delta W\) benutzt man dann auch ein \(dW\):
\[ W = \int dW \]
\[ W_{in} = \int_1^2 p(V) \; dV \]
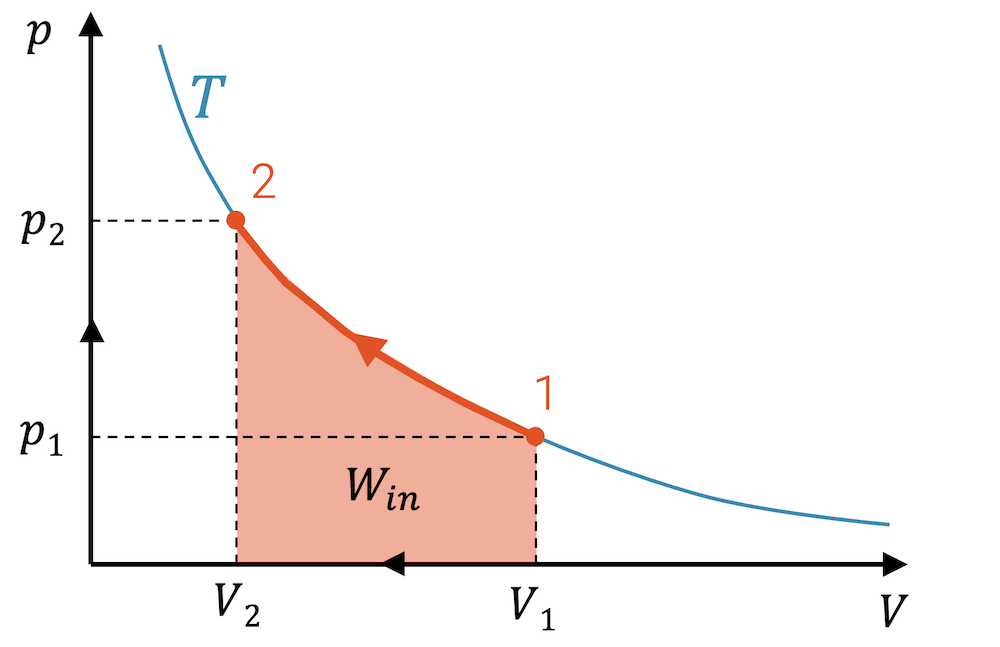
Wenn das Komprimieren von 1 nach 2 die Arbeit \(W_{in}\) erfordert, dann können wir uns auch den umgekehrten Fall denken. Das Fluid agiert wie eine Feder und statt von aussen komprimiert zu werden, ist es schon komprimiert und gibt seine Spannarbeit ab:
\[ W_{out} = \int_2^1 p(V) \; dV \]
Das Fluid gibt Arbeit ab und entspannt dabei.
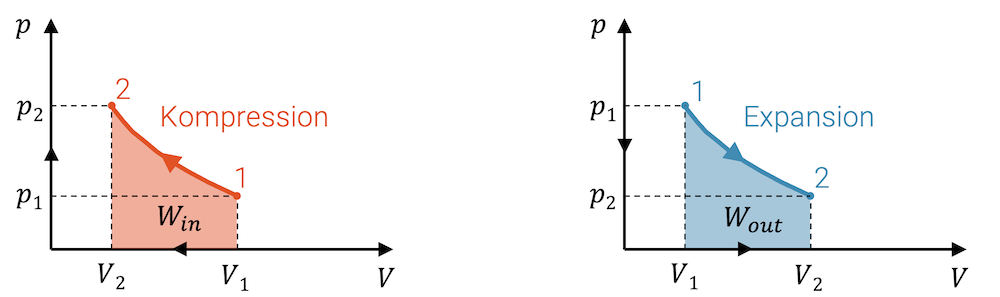
Bei einer beliebigen Zustandsänderung, bei welcher das Fluid komprimiert wird, entspricht die Fläche unter der Linie der Zustandsänderung im p,V-Diagramm der eingebrachten Kompressionsarbeit \(W_{in}\), die am Fluid dafür verrichtet worden ist.
Wird das Fluid entspannt und gibt es dabei Expansionsarbeit ab, so kann diese Arbeit \(W_{out}\) ebenfalls als Fläche im p,V-Diagramm abgelesen werden.
Arbeit von Kreisprozessen
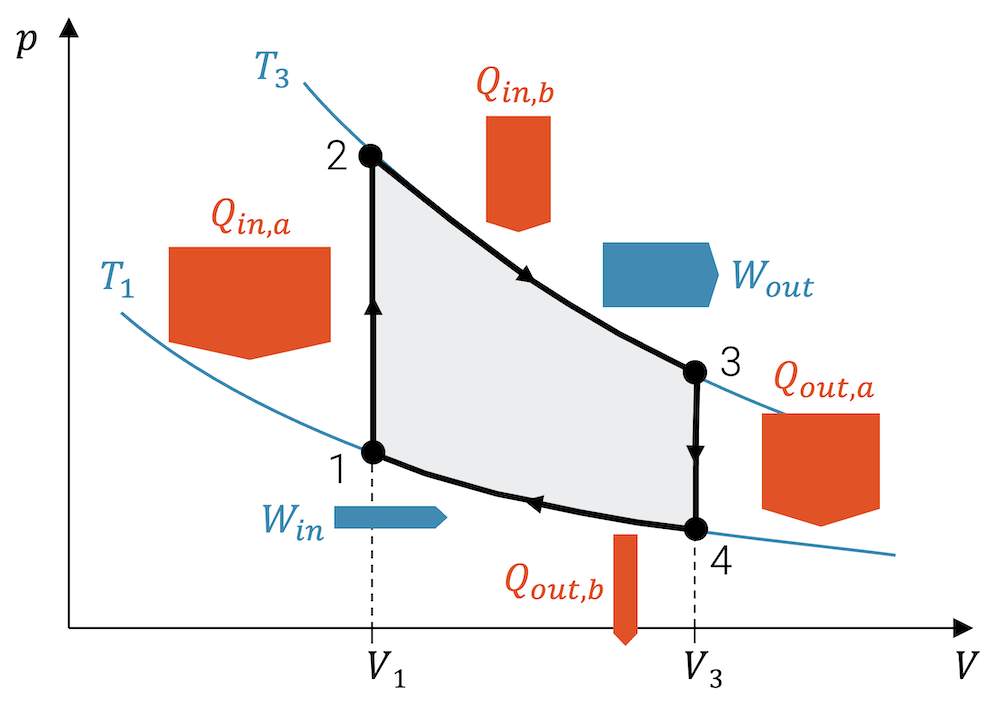
In Wärmekraftmaschinen (WKM) durchläuft ein Fluid einen sog. Kreisprozess, in welchem am Ende das Fluid wieder in den anfänglichen Zustand geführt wird. Einen solchen Kreisprozess können wir erhalten mit den folgenden Zustandsänderungen:
1 ➝ 2 : Isotherme Kompression (\(W_{in}\))
2 ➝ 3 : Isochore Wärmeaufnahme
3 ➝ 4 : Isotherme Expansion (\(W_{out}\))
4 ➝ 1 : Isochore Wärmeabgabe
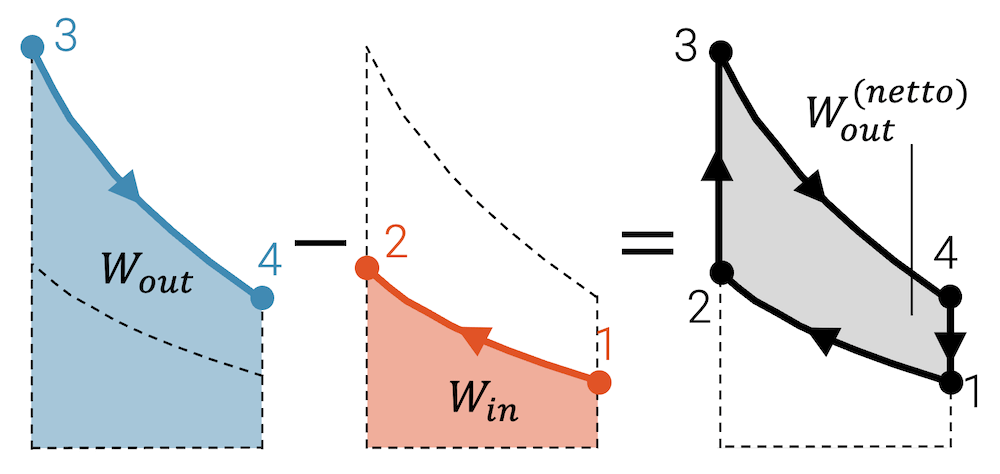
Wenn wir uns nun die durch den Kreisprozess eingeschlossene Fläche anschauen, dann entspricht sie der Differenz der vom Fluid abgegebenen und aufgenommenen Arbeit:
\[ W_{out}^{(netto)} \; = \; W_{out} – W_{in} \]
Wenn mehr Arbeit abgeführt als eingebracht wird, dann ist das energetisch eigentlich nicht möglich oder nicht nachhaltig. Allerdings werden ja in den Zustandsänderungen 2 \(^\rightarrow\) 3 und 4 \(^\rightarrow\) 1 Wärme aufgenommen bzw. abgegeben. Insgesamt muss die Bilanz der Energieströme stimmen und die Wärmekraftmaschine muss gleich viel Energie aufnehmen, wie sie abgibt. Die eingeschlossene Fläche zeigt uns aber die wichtigste Grösse der Wärmekraftmaschine, nämlich wie viel Arbeit sie abgibt. Das ist nämlich auch ihr Job. Wärmekraftmaschinen dienen dazu, Arbeit abzugeben, die sie zuvor in Form von Wärme aufgenommen haben.
Die eingeschlossene Fläche zeigt bei einem Kreisprozess (Uhrzeigersinn im p,V-Diagramm) die Netto-Arbeit, die das Fluid abgibt.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Kommentar oder Frage schreiben
Du musst angemeldet sein, um einen Kommentar abzugeben.