
Unter Interferenz verstehen wir die Überlagerung von (meist) zwei gleichen Wellen mit leichten Verschiebungen in der Phase, so dass wir eine gegenseitige Verstärkung (konstruktive Interferenz) oder eine gegenseitige Auslöschung (destruktive Interferenz) beobachten können.
Die Phasenverschiebungen können verschiedene Ursachen haben: Zum einen kann die Wellengeschwindigkeit für die eine Welle leicht grösser oder kleiner sein, zum anderen ist auch ein kleiner Unterschied beim eigentlichen Weg möglich, so dass die eine Welle früher dran ist als die andere.
Meistens wechseln konstruktive und destruktive Interferenz ab, so dass typische Interferenzmuster entstehen mit hellen und dunklen Streifen oder Ringen.
Konstruktive Interferenz
Wenn zwei gleiche, exakt synchrone Wellen aufeinander treffen, entsteht kurzzeitig eine Verstärkung der Wellenberge, d.h. wir beobachten eine Verdoppelung der Wellenberge und eine Verdoppelung der Wellentäler.
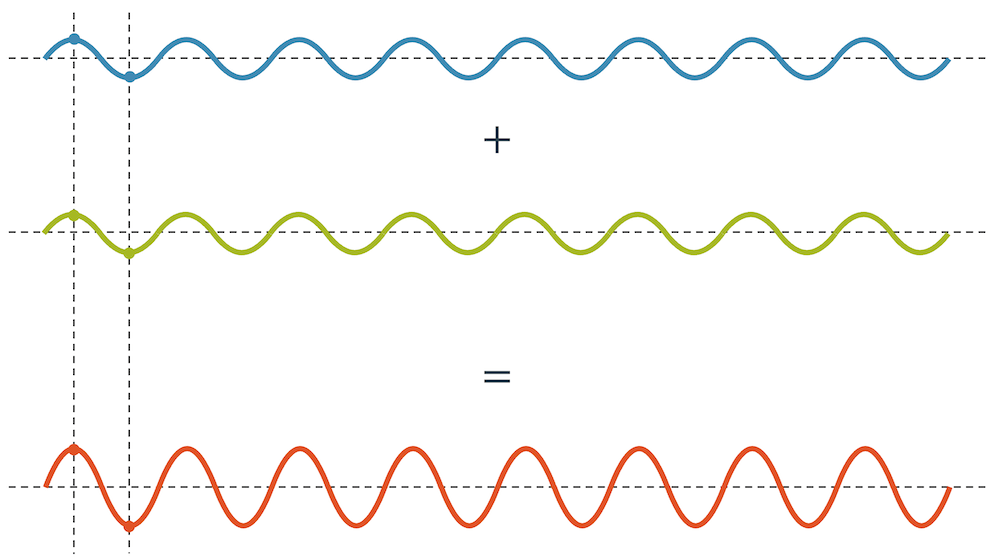
Diese Form der Wellenüberlagerung heisst konstruktive Interferenz. Beide Wellen verstärken sich gegenseitig.
Mathematisch ausgedrückt heisst das: Aus zwei Sinusfunktionen entsteht eine Sinusfunktion mit summierter Amplitude:
\[ f_1(x,t) = A_1 \cdot \sin(kx – \omega t) \]
\[ f_2(x,t) = A_2 \cdot \sin(kx – \omega t) \]
\[ f_1(x,t) + f_2(x,t) = (A_1 + A_2) \cdot \sin(kx – \omega t) \]
Bei der konstruktiven Interferenz verstärken sich beide Wellen, da Wellenberge auf Wellenberge auftreffen und Wellentäler auf Wellentäler. Dazu müssen die beiden Wellen aber genau synchron sein. Die Amplituden werden summiert, so dass die Berge höher und die Täler tiefer werden.
Destruktive Interferenz
Wenn die beiden gleichen Wellen sich überlagern, sie jedoch nicht synchron, sondern exakt um eine halbe Wellenlänge \(\frac{\lambda}{2}\) verschoben sind, passiert etwas unglaubliches!
Die Wellenberge der einen Welle werden mit einem Wellental der anderen Welle überlagert und umgekehrt. Mathematisch löschen sich alle Berge und Täler auf!
Die beiden Wellen, die sich vorhin zu einer doppelt so starken Welle aufsummiert hatten, löschen sich jetzt plötzlich gegenseitig auf, d.h. wir sind von 200% auf 0% gekommen, einfach nur durch eine Verschiebung um \(\frac{\lambda}{2}\).
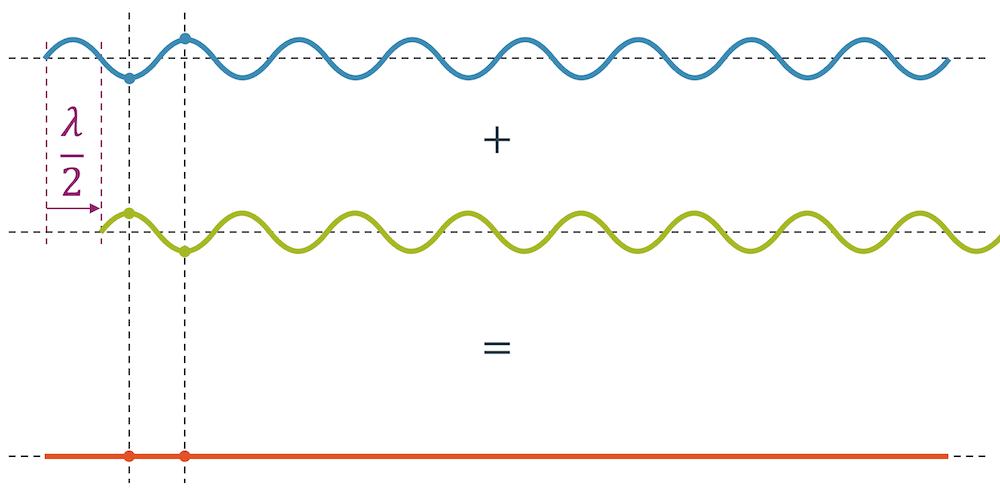
Wir erkennen natürlich, dass eine noch grössere Verschiebung um \(\lambda\) wieder zu einer Verstärkung, d.h. wieder zu 200% führt.
Die Auslöschung zweier Wellen sieht mathematisch wie folgt aus:
\[ f_1(x,t) = A \cdot \sin(kx – \omega t) \]
\[ f_2(x,t) = A \cdot \sin\Big(k \cdot \big(x-\frac{\lambda}{2}\big) – \omega t\Big) \]
Bei der zweiten Wellen müssen wir in der Funktion etwas aufräumen. Zuerst können wir ausmultiplizieren:
\[ k \cdot \big(x-\frac{\lambda}{2}\big) – \omega t \;=\; kx – \frac{k\lambda}{2} -\omega t \]
Das zweite \(k\) ersetzen wir mit der Definition der Wellenzahl \(k=\frac{2\pi}{\lambda}\).
\[ \require{cancel} \frac{k \lambda}{2} = \frac{\cancel{2}\pi \cancel{\lambda}}{\cancel{\lambda} \cdot \cancel{2}} = \pi \]
Damit kriegen wir:
\[ f_2(x,t) = A \cdot \sin(kx – \pi – \omega t) \]
Für den Zeitpunkt \(t=0\) gilt somit:
\[ f_1(x,0) = A \cdot \sin(kx) \]
\[ f_2(x,0) = A \cdot \sin(kx – \pi) \]
Jetzt benutzen wir die Identität \(\sin(\alpha – \beta) = \sin(\alpha) \cos(\beta) – \cos(\alpha) \sin(\beta)\)
\[ f_2(x,0) = A \cdot \Big( \sin(kx) \cos(\pi) – \cos(kx) \sin(\pi) \Big) \]
Wir ersetzen \(\cos(\pi) = -1\) und \(\sin(\pi) = 0 \( und erhalten:
\[ f_2(x,0) = -A \cdot \sin(kx) \]
Wir sehen, dass beide Funktionen sich in Summe aufheben:
\[ f_1(x,t) + f_2(x,t) = (A-A) \cdot \sin(kx – \omega t) = 0 \]
Die beiden Wellen löschen sich gegenseitig aus.
Michelson-Interferometer
Mit einem Interferometer wird Interferenz bewusst erzeugt. Beim Michelson-Interferometer wird eine Lichtwelle durch einen semi-transparenten Spiegel aufgeteilt. Wir können uns das wie bei einer Glasscheibe vorstellen: Ein Teil der Lichts geht durch die Glasscheibe durch, ein anderer Teil wird an ihr reflektiert.
Dadurch wird die ursprüngliche Welle in zwei identische Wellen aufgeteilt. Mit Hilfe von Spiegeln werden die Strahlen wieder zurückreflektiert, bis sie beide am gleichen Ort auf dem Sensor auftreffen. Die beiden gleichen Wellen werden demnach auf dem letzten Teilstück einander überlagert.
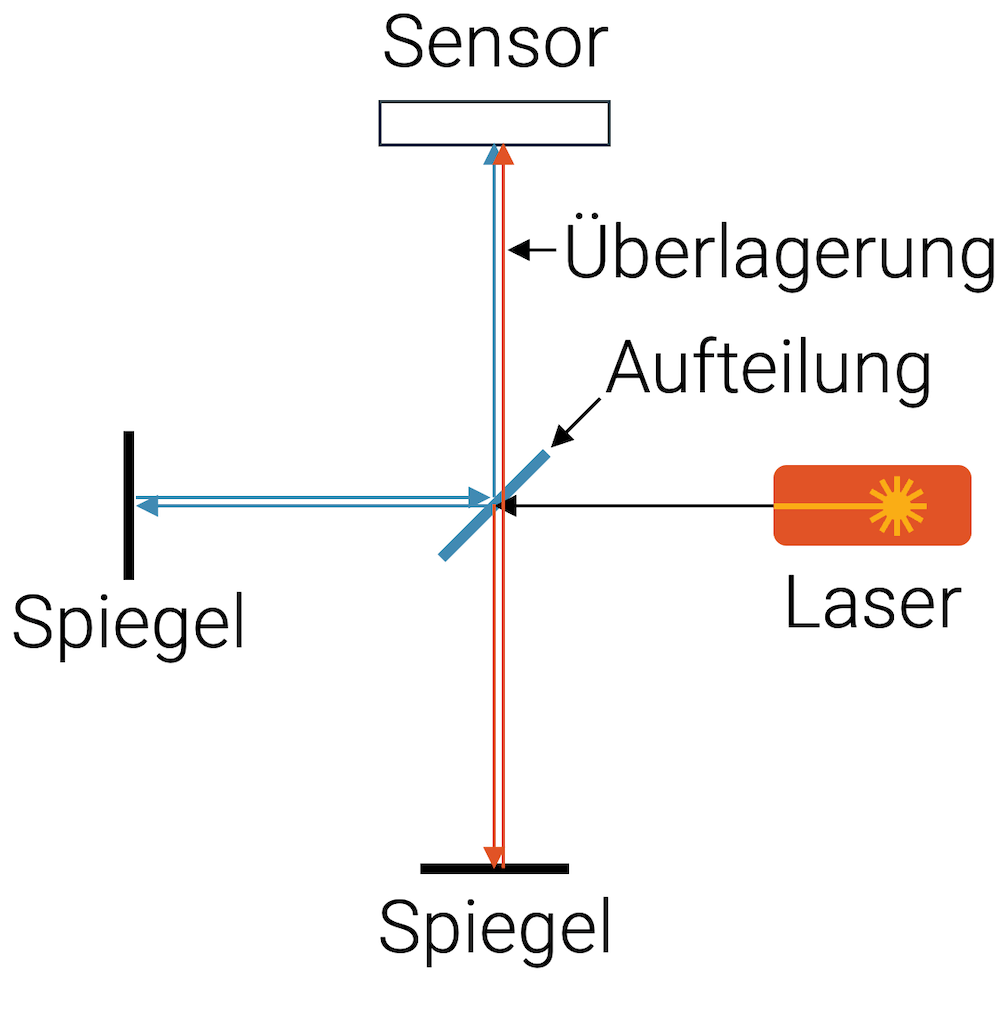
Ist der Weg der beiden Lichtstrahlen exakt gleich lang, kommen die beiden Strahlen wieder gleichzeitig zusammen und interferieren konstruktiv, d.h. sie erzeugen wieder den Lichtstrahl, der ursprünglich von der Quelle emittiert worden ist.
Wenn der Weg des einen Strahls aber etwas länger oder kürzer ist als der andere, sind die beiden Wellen phasenverschoben. Sind die beiden Wellen exakt um eine halbe Wellenlänge \(\frac{\lambda}{2}\) verschoben, haben wir ideale destruktive Interferenz und der Sensor registriert keine Welle, obwohl beide Wellen bei ihm eintreffen!
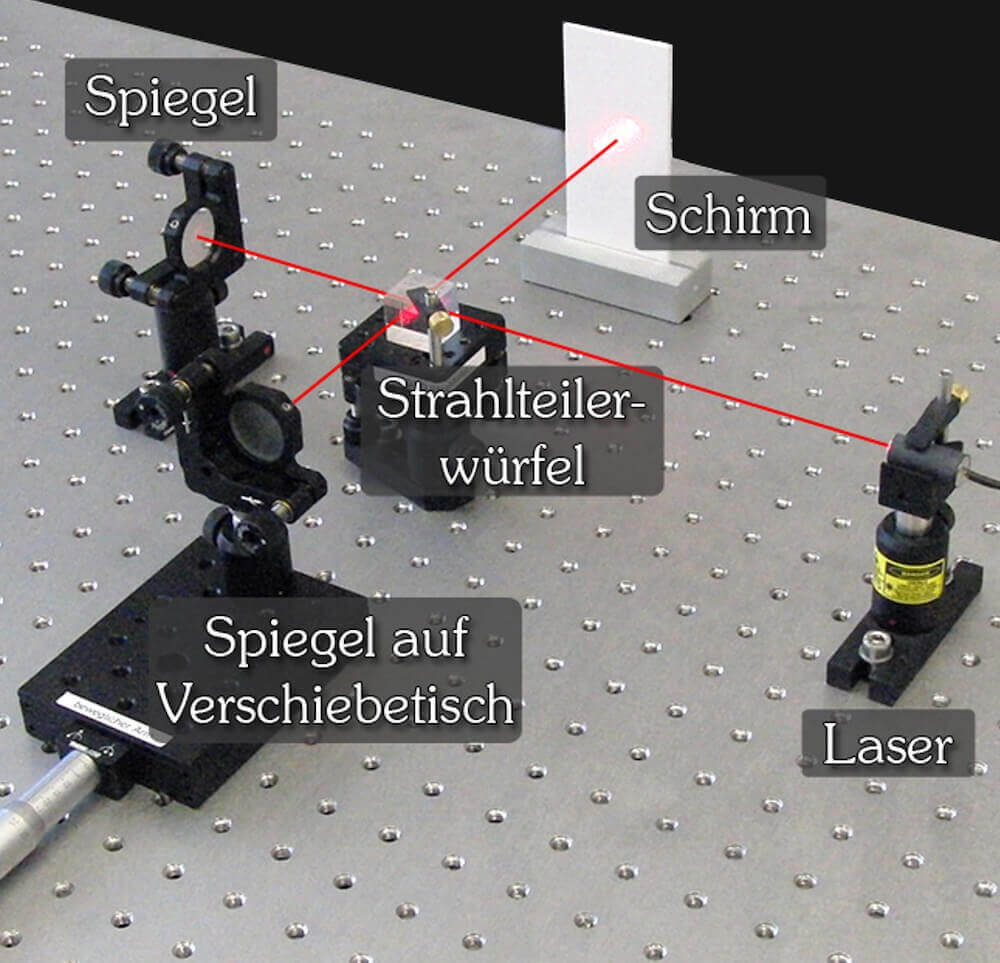
Da die Strahlen auf dem letzten Abschnitt nicht alle 100%-ig genau parallel verlaufen, gibt es Strahlen, die gegen aussen bereits etwas mehr Weg hinter sich gebracht haben als andere. Wenn das Interferometer so eingestellt ist, dass die beiden Strahlen konstruktiv interferieren, so werden sie am Rand doch auch destruktiv interferieren. Dadurch entstehen dunkle Ringe, die dann wieder von hellen Ringen abgelöst werden usw.

Mit einem Michelson-Interferometer können verschiedene Experimente durchgeführt werden. Beispielsweise kann die Wellenlänge des Lichts bestimmt werden, indem die Verschiebung der Spiegel von einem Maximum zum nächsten gemessen wird.
Einer der beiden Strahlen kann beispielsweise auch durch eine Probe durchlaufen. Die Interferenz sagt dann etwas darüber aus, um wie viel der Lichtstrahl in der Probe abgebremst worden ist (Brechungsindex).
Michelson-Morley-Experiment
Im Jahr 1887 untersuchten die beiden amerikanischen Physiker Albert A. Michelson und Edward W. Morley mit Hilfe eines solchen Interferometers die Gegenwart des sog. Aethers. Unter dem Aether verstand man eine Art Substanz, die die Ausbreitung von elektromagnetischen Wellen ermöglichen würde. Schallwellen brauchen Luft oder sonst einen Stoff, Seilwellen brauchen ein Seil, Erdbebenwellen sind auf die Erdkruste angewiesen, um sich ausbreiten zu können, Wasseroberflächenwellen machen ohne Wasser keinen Sinn etc. Es wurde deshalb vermutet, dass auch elektromagnetische Wellen für ihre Ausbreitung einen Stoff, den Aether, bräuchten.
Die Idee war, dass die Erde sich im Universum bewegt und dadurch einen gewissen Aether-Fahrtwind spüren sollte, so dass Licht mit Gegenwind langsamer sein sollte als Licht mit Rückenwind. Das Michelson-Interferometer zeigte aber keine Abweichung, egal wie es ausgerichtet war. Selbst im Jahr 2009 wurde nochmals und viel genauer gezeigt, dass die Geschwindigkeit des Lichts unabhängig von seiner Richtung im Universum ist. Wir können deshalb davon ausgehen, dass es vermutlich keinen Aether gibt.
Fabry-Pérot-Interferometer
Das nach den beiden französischen Physikern Charles Fabry und Alfred Perot benannte Interferometer arbeitet nur mit einer Achse. Ein monochromatischer Lichtstrahl (eine Wellenlänge) tritt durch einen teilweise durchlässigen Spiegel in den Zwischenraum ein.
Am anderen Ende ist wieder ein teilweise durchlässiger Spiegel angebracht, so dass der Strahl zurück zum Eingang reflektiert wird. Hier wird der Lichtstrahl nochmals reflektiert und wandert jetzt wieder in der ursprünglichen Richtung. Er überlagert sich mit dem Strahl, der erst gerade eingetreten ist.
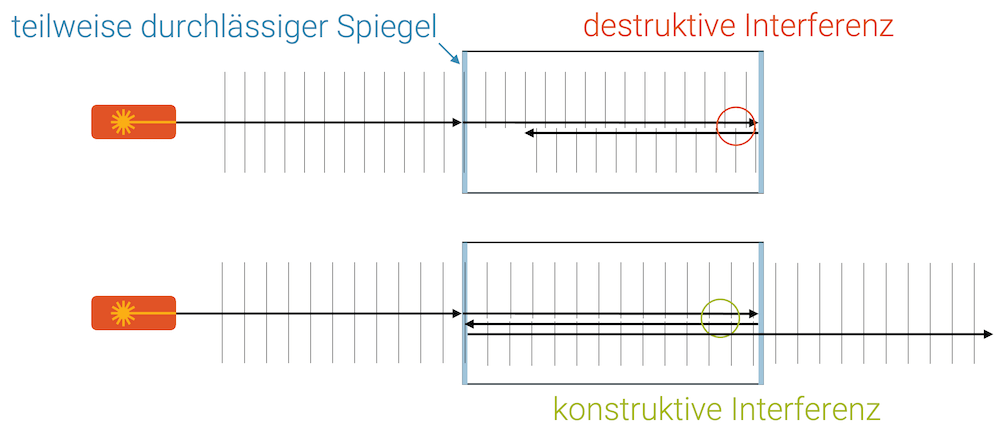
Wenn die beiden Strahlen konstruktiv interferieren, kann die Welle teilweise austreten. Wenn die Strahlen aber destruktiv interferieren, gibt es eigentlich nichts mehr zum Durchlassen, da die Welle ausgelöscht ist!
Ein Fabry-Perot-Interferometer ist ein Filter für Wellenlängen. Bei konstruktiver Interferenz kommt die Welle wieder raus. Bei anderen Frequenzen nicht. Mit der Wahl der richtigen Baugrösse kann gewählt werden, welche Wellenlängen durchgelassen werden sollen und welche nicht.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.