Inhalt
Das Wichtigste in Kürze
Der Brechungsindex \(n\) ist mehrheitlich eine Materialgrösse, der von der chemischen Zusammensetzung und der Kristallstruktur abhängt. Er gibt an, um welchen Faktor die Geschwindigkeit des Lichts im Medium \(u\) im Vergleich zur maximal möglichen Lichtgeschwindigkeit im Vakuum \(c_0\) verlangsamt ist:
\[ u = \frac{c}{n} \]
Trifft Licht auf eine Grenzfläche eines Mediums mit anderem Brechungsindex, so verändert sich die Wellenlänge und es entsteht das Phänomen der Brechung.
Der Brechungsindex ist aber auch leicht abhängig von der Frequenz bzw. Wellenlänge (Farbe) des Lichts, was erklärt, warum weisses Licht als Gemisch aller Regenbogenfarben in einem Prisma aufgeteilt wird.
Videos
-
Brechung – Lichtgeschwindigkeit in Medien (0009)
Du musst dich hier einloggen, um das Video anzusehen. Noch kein Login?
-
Brechung – Berechnung Brechungswinkel (0010)
Du musst dich hier einloggen, um das Video anzusehen. Noch kein Login?
-
Auge – Scharfe Sicht (0144)
Dauer: 15 min 45 s
Du musst dich hier einloggen, um das Video anzusehen. Noch kein Login?
Definition
Für den Brechungsindex \(n\) sind auch andere Bezeichnung üblich:
- Brechzahl oder Brechungszahl
- optische Dichte
- refraktiver Index
Der Brechungsindex \(n\) gibt an, um welchen Faktor die Wellengeschwindigkeit des Lichts im betreffenden Material verlangsamt ist, verglichen zur maximalen Lichtgeschwindigkeit im Vakuum \(c_0\):
\[ c_0 = 2.998 \cdot 10^8\;\text{m/s} \]
Lichtgeschwindigkeit in einem Medium mit Brechungsindex \(n\):
\[ u = \frac{c_0}{n} \]
Beispielsweise bedeutet ein Brechungsindex \(n=2\), dass Licht um den Faktor 2 verlangsamt ist, wenn es sich in diesem Material fortbewegt.
Da die Lichtgeschwindigkeit im Vakuum die physikalisch grösstmögliche Geschwindigkeit in der Raumzeit darstellt, gibt es keine Brechungsindizes, deren Betrag kleiner als 1 ist:
\[ |n| > 1 \]
Der Brechungsindex ist weitgehend abhängig von der chemischen Zusammensetzung und der Struktur (z.B. Kristallstruktur) des Materials. Es gibt auch spezielle Materialien mit negativem Brechungsindex, die Licht in die andere als erwartete Richtung brechen. 😮
Brechungsindizes verschiedener Materialien
In der nachfolgenden Tabelle sind die Brechungsindizes verschiedener Materialien aufgelistet:
| Material | Brechungsindex \(n\) |
| Vakuum | 1 (exakt) |
| Luft | 1.0003 \(\approx\) 1 |
| Wasser | 1.33 |
| Glycerin | 1.47 |
| Fensterglas | 1.52 |
| Diamant | 2.42 |
Einfluss auf die Brechung
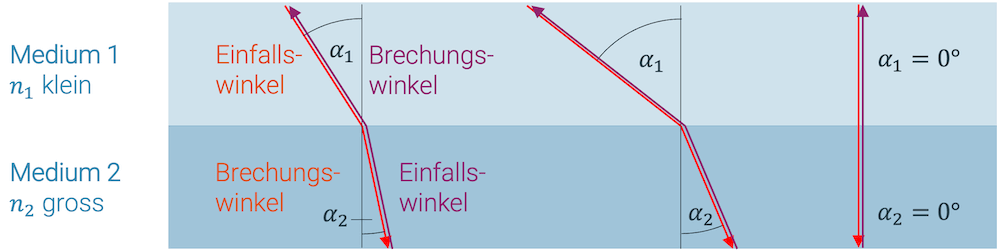
Trifft Licht auf eine Grenzfläche zu einem Medium mit anderem Brechungsindex, so verändert sich die Wellenlänge und es entsteht das Phänomen der Brechung.
Je nach Einfallswinkel \(\alpha_1\) im Medium 1 schlägt das Licht im Medium 2 einen anderen Brechungswinkel \(\alpha_2\) ein. Es gilt das Brechungsgesetz von Snellius:
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{n_2}{n_1} \]
“Weisses Licht ist die Mischung aller Farben. Ein Prisma fächert dieses Licht in seine Bestandteile auf.”
Abhängigkeit von der Frequenz (Dispersion)
Spätestens seit dem Album Dark Side of the Moon der britischen Rockband Pink Floyd im Jahr 1973 ist allen bekannt, dass ein weisser Lichtstrahl in einem Prisma in die Regenbogenfarben aufgeteilt wird.
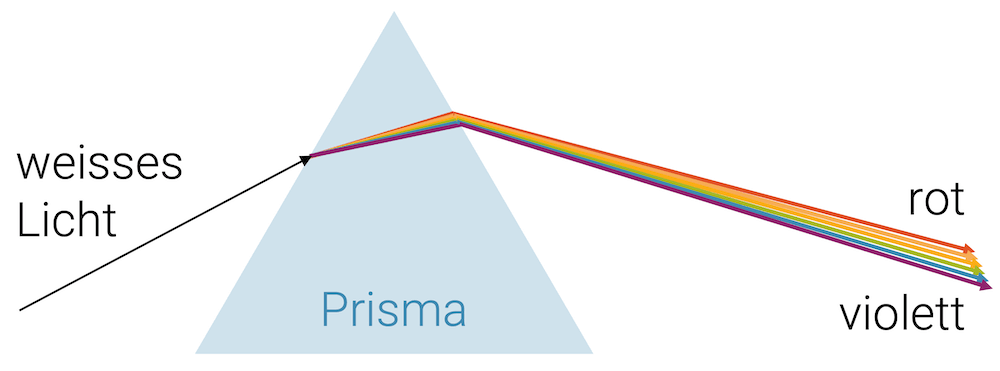
Weisses Licht ist die Mischung von Lichtstrahlen mit allen sichtbaren Frequenzen bzw. Wellenlängen. Tatsächlich fächert ein Prisma dieses Licht in seine Bestandteile auf.
Das hat damit zu tun, dass der Brechungsindex meistens abhängig von der Frequenz \(f\) bzw. Wellenlänge \(\lambda\) des Lichts ist und damit auch abhängig von der Farbe des Lichts. Das Aufteilen der verschiedenen Wellenbestandteile heisst Dispersion.
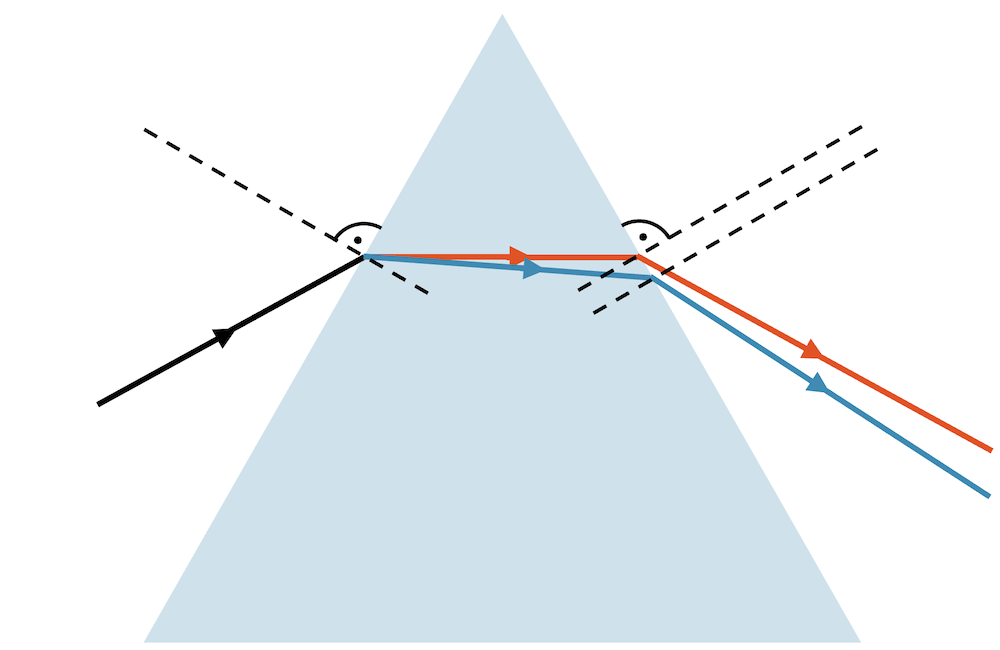
Unterschiedliche Farben werden verschieden stark gebrochen werden. Im Glasprisma ist langwelliges rotes Licht etwas weniger verlangsamt als kurzwelliges blaues Licht. Der Brechungsindex von Glas ist für rotes Licht deshalb leicht kleiner als für blaues Licht, so dass blaues Licht stärker gebrochen wird als rotes Licht. In Quarzglas gilt beispielsweise:
- rotes Licht hat einen Brechungsindex von \(n >1.45\)
- blaues Licht hat einen Brechungsindex von \(n = 1.47\)
- alle anderen Farben haben einen Brechungsindex zwischen diesen beiden Extremen
Für die anderen Farben liegen die Brechungsindizes zwischen den beiden Extremen, so dass das Prisma das weisse Licht in alle Regenbogenfarben aufteilt. 🌈
Im nachfolgenden Diagramm ist der Brechungsindex für Licht in Quarzglas aufgezeichnet, abhängig von der Wellenlänge des Lichts. Das Diagramm umfasst das Spektrum von UV-Strahlen bei 200 nm bis hin zu Infrarot bei einer Wellenlänge von 1’400 nm.
Wir sehen, dass der Brechungsindex zwischen 1.54 und 1.45 schwankt. Er variiert damit um ein paar wenige Prozente, was aber für eine feine Aufteilung des Lichts aufgrund abweichender Brechungswinkel ausreicht.
Beispiel
-
- rotes Licht hat einen Brechungsindex von \(n = 1.45\)
- blaues Licht hat einen Brechungsindex von \(n = 1.47\)
Aufgabensammlung
-
Lichtgeschwindigkeit in Medien (0009)
2 Teilaufgaben mit Lösungen (pdf/Video):
• Berechnung der Lichtgeschwindigkeit in Medien
• BrechungsindexDu musst dich hier einloggen, um zur Aufgabe zu gelangen.
Noch kein Login?
-
Scharfe Sicht (0144)
3 Teilaufgaben mit Lösungen (pdf/Video):
• Brennweiten berechnen für Fern- und für Nahsicht
• Unscharfe Sicht unter WasserDu musst dich hier einloggen, um zur Aufgabe zu gelangen.
Noch kein Login?
Lernziele
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt
Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.