Totalreflexion

Die Totalreflexion ist ein typisches Wellenphänomen, das v.a. bei Licht ausgenutzt wird. Wenn der Lichtstrahl in einem optisch dichteren Medium (mit grösserem Brechungsindex) relativ flach auf die äussere Grenzfläche auftrifft, so vermag er nicht aus dem Medium auszutreten und reflektiert total im Medium gemäss dem Reflexiongesetz.

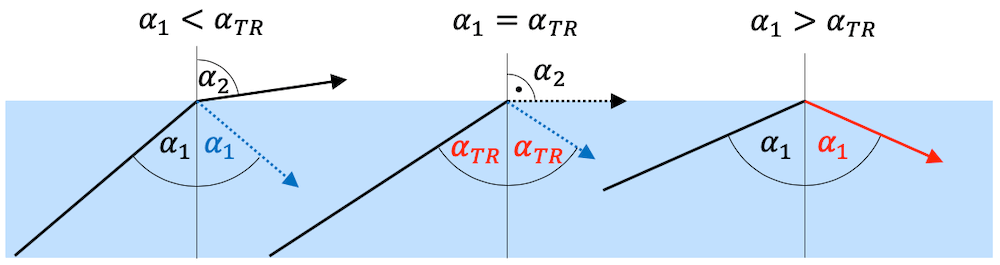
Betrachten wir einen Lichtstrahl der in einem Medium verläuft mit einem grösseren Brechungsindex als demjenigen des umgebenden Mediums (links). Wenn dieser Strahl relativ steil auf die Grenzfläche auftrifft, d.h. unter einem kleinen Einfallswinkel \(\alpha_1\), so verlässt der Strahl das Medium 1 gemäss dem Brechungsgesetz unter einem grösseren Brechungswinkel \(\alpha_2\).

Wenn wir den Einfallswinkel vergrössern, erreichen wir irgendwann die kritische Situation (Mitte), in welcher wir einen maximalen Brechungswinkel von \(\alpha_2 = 90^\circ\) erreichen. In dieser Situation ist der Einfallswinkel minimal für die Erreichung der Totalreflexion. Wir nennen diesen minimalen Einfallswinkel deshalb \(\alpha_{TR}\).

Es leuchtet ein, dass eine weiteres Vergrössern des Einfallswinkels (rechts) eigentlich zu einem stumpfen Brechungswinkel führen müsste, der den Strahl wieder in das Medium 1 zurückzwingt. Genau das passiert im Fall der Totalreflexion, wenn für den Einfallswinkel gilt: \(\alpha_1 > \alpha_{TR}\).

 Beispiel

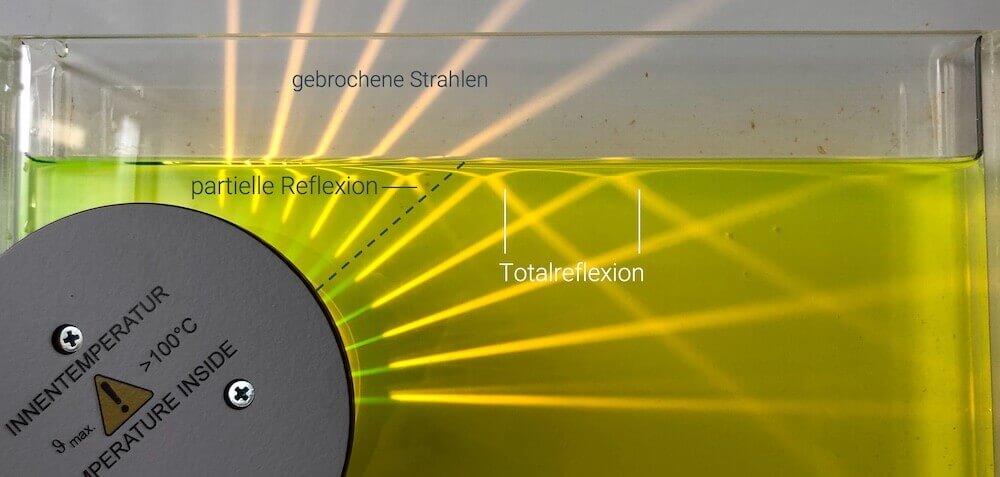
Dieses Experiment zeigt uns, wie Lichtstrahlen in einem Bereich über der Lichtquelle aus dem Wasser austreten (Brechung). Ein kleiner Teil wird jedoch reflektiert (klassische, partielle Reflexion). Links und rechts aussen ist der Einfallswinkel jedoch grösser als der kritische Winkel \(\alpha_{TR}\) und wir beobachten Totalreflexion.

 Beispiel 

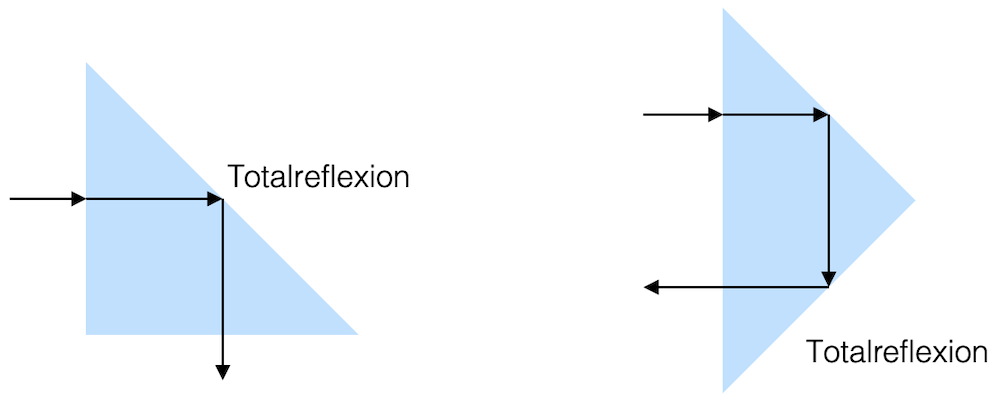
Prismen aus Glas werden oft als Spiegelersatz eingesetzt. Um den kritischen Winkel für die Totalreflexion zu berechnen, brauchen wir die Brechungsindizes: Medium 1 ist Glas (\(n_1 = 1.52\)), Medium 2 ist Luft (\(n_2 = 1\)).

\[ \alpha_{TR} = \sin^{-1} \left( \frac{n_2}{n_1} \right) = \sin^{-1} \left( \frac{1}{1.52} \right) = 41.1^\circ \]

Wenn wir mit einem Einfallswinkel \(\alpha_1 = 45^\circ\) auf die Grenzfläche von Glas zu Luft auftreffen, haben wir Totalreflexion im Glas, da der Einfallswinkel \(\alpha_1\) grösser als der kritische Winkel \(\alpha_{TR}\) ist.

Herleitung

Im kritischen Fall (obige Grafik, Mitte) hat der Einfallswinkel den kritischen Wert \(\alpha_1 = \alpha_{TR}\) und der Brechungswinkel beträgt \(\alpha_2 = 90^\circ\). Wir setzen für diesen Fall das Brechungsgesetz an:

\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{\sin(\alpha_{TR})}{\sin(90^\circ)} = \frac{n_2}{n_1} \]

Nun wissen wir, dass \(\sin(90^\circ)=1\). Wir erhalten deshalb:

\[ \sin(\alpha_{TR}) = \frac{n_2}{n_1} \]

Schliesslich setzen wir die Gleichung beidseitig in die Arkussinus-Funktion ein. Wir wissen, dass damit der Sinus auf der linken Seite verschwinden wird:

\[ \sin^{-1}(\sin(\alpha_{TR})) = \alpha_{TR} = \sin^{-1} \left( \frac{n_2}{n_1} \right) \]