Zusammengesetzte Bewegungen

Geschwindigkeiten sind Vektorgrössen, d.h. wenn mehrere Bewegungen zusammengesetzt bzw. überlagert sind, werden die Geschwindigkeiten dieser Bewegungen als Vektoren addiert.

Wenn z.B. eine Person im Zug nach vorne geht und der Zug selber auch fährt, addieren sich die Gehgeschwindigkeit und Fahrgeschwindigkeit des Zugs.

Überlagerung von Geschwindigkeiten in einer Dimension

Das Beispiel der Person im Zug ist im wesentlichen eine eindimensionale Situation. Die beiden Geschwindigkeiten addieren sich zu der sog. Summengeschwindigkeit: Die Person bewegt sich gegenüber der Erde schneller als der Zug!

Überholt der Zug einen

Wenn zwei überlagerte Geschwindigkeiten parallel sind, so werden ihre Beträge im gleichgerichteten Fall addiert: Summengeschwindigkeit. Im entgegengesetzten Fall werden sie subtrahiert: Differenzgeschwindigkeit. Als Vektoren behandelt, entsprechen beide Fälle (auch die Subtraktion) einer Vektoraddition. Die totale Geschwindigkeit ist die Vektorsumme von Geschwindigkeiten:

\[ \vec{v_{tot}}=\vec{v_1} + \vec{v_2}\]

Beim River Surfing wird normalerweise eine stehende Welle ausgenutzt. In diesem Fall hält sich der Sportler mit einem Seil an der Brücke. Gegenüber dem Wasser hat er eine Relativgeschwindigkeit \(v_R\), als würde er von einem Boot gezogen. Das Wasser selber hat die gleiche Geschwindigkeit \(v_W\), nur in die entgegengesetzte Richtung. Werden beide Geschwindigkeiten als Vektoren addiert, so heben sie sich auf. Der Sportler hat gegenüber dem Boden keine Geschwindigkeit.

Wenn Flugzeuge bei starkem Seitenwind landen, erkennen wir, dass sie “schräg” fliegen. Gegenüber der Luft fliegen sie schon gerade, denn sonst hätten sie ja schon im Flug Seitenwind. Das haben sie aber nicht. Sie bewegen sich aber mit den Luftmassen seitlich. Das Flugzeug ist Teil des Winds, solange es in der Luft ist. Gegenüber dem Boden bewegt es sich vorwärts, wegen der Triebwerke und seitlich wegen des Winds. Bei der Landung muss diese Schräglage korrigiert werden.

Parallele Geschwindigkeiten

Wenn wir zwei parallele Vektoren addieren, stellt sich nur die Frage, ob sie gleich gerichtet oder entgegengesetzt gerichtet ist. Im ersten Fall addieren sich die Geschwindigkeiten. Wenn wir in einem Zug, der mit 100 km/h fährt in Fahrtrichtung mit 5 km/h den Gang entlang gehen, ist unsere Geschwindigkeit gegenüber dem Boden 105 km/h. Man spricht in diesem Zusammenhang auch von der Summengeschwindigkeit.

Sind die beiden Geschwindigkeiten einander entgegengesetzt, reduziert die eine Geschwindigkeit den Effekt der anderen. Wir bilden die Differenz und sprechen deshalb auch von der Differenzgeschwindigkeit.

Beispiel

Ein Flugzeug fliegt mit relativen Geschwindigkeit von \(v_R\) = 900 km/h gegenüber der umgebenden Luft. Die Luft selber strömt in Form von Wind in die gleiche Richtung mit \(v_W\) = 50 km/h. Was ist die Geschwindigkeit des Flugzeugs gegenüber dem Boden?

Welche Geschwindigkeit hat das Flugzeug, wenn es mit gleicher Geschwindigkeit gegen den Wind fliegt?

---

Im ersten Fall fliegt das Flugzeug mit dem Wind. Da die Vektoren \(\vec{v_R}\) und \(\vec{v_W}\) gleich gerichtet sind, addieren sich ihre Beträge und wir erhalten die Summengeschwindigkeit \(v_{F1}\) = 950 km/h.

Im zweiten Fall fliegt das Flugzeug gegen den Wind. Für “900 Schritte nach vorn, bewegt der Wind es mit 50 Schritten wieder nach hinten”, d.h. die Vektorsumme \(\vec{v_R} + \vec{v_W}\) führt zur Subtraktion der Beträge. Wir erhalten so die Differenzgeschwindigkeit: \(v_{F2}\) = 850 km/h.

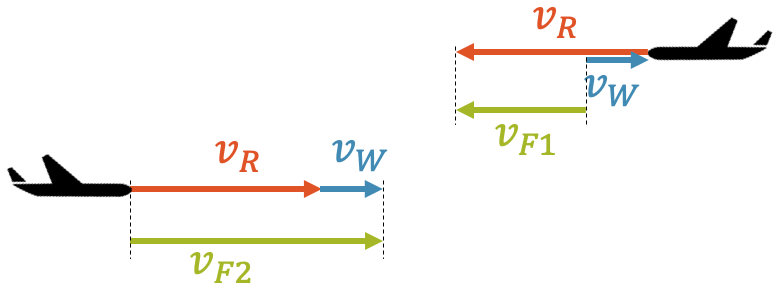
Überlagerung von Geschwindigkeiten in zwei Dimensionen

Beispiel: Nicht-parallele Geschwindigkeiten

Bei nicht parallelen Geschwindigkeiten, addieren sich die Geschwindigkeiten wie Vektoren. Am besten kann die resultierende Vektorsumme grafisch dargestellt werden.

Ein Kanu bewegt sich mit der gleichen Rudergeschwindigkeit \(v_R\) relativ zum Wasser. Mit welcher Absolutgeschwindigkeit bewegt sich das Kanu gegenüber dem Boden in den folgenden vier Fällen:

• mit dem Fluss
• gegen die Flussrichtung
• senkrecht zur Flussrichtung, so dass der Fluss rechts abfliesst
• senkrecht zur Flussrichtung, so dass der Fluss links abfliesst

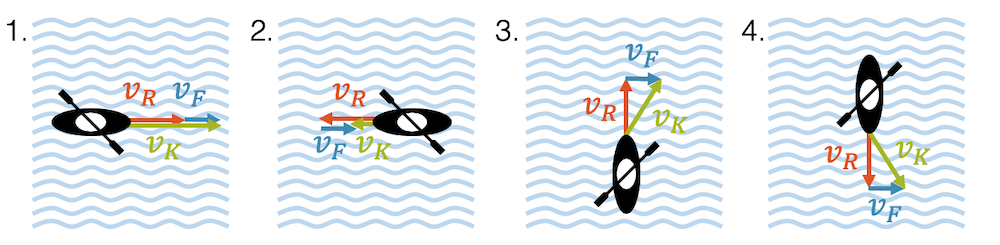
Beachte, dass in den beiden letzten Fällen, das Kanu sich leicht seitwärts bewegt, ähnlich zu einem Flugzeug, das bei Seitenwind landet.

Zusammengesetzte Bewegungen wieder aufteilen

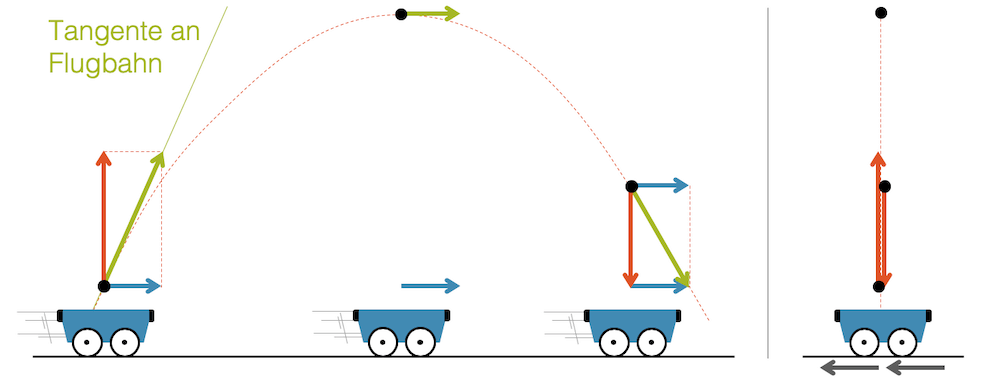
Die obige Skizze gehört zu einem netten Experiment: Ein kleiner Wagen, bewegt sich von links nach rechts. Eine Vorrichtung macht, dass er eine Kugel senkrecht nach oben abschiesst. Die Kugel fliegt parabelförmig und landet wieder exakt auf dem Wagen. Besonders eindrücklich wird dies, wenn der Wagen zwischenzeitlich in einen Tunnel fährt.

Warum trifft die Kugel den rollenden Wagen so zielsicher? Wir müssen nur die Bewegung der Kugel als eine zusammengesetzte Bewegung betrachten: Einerseits hat sie die gleiche seitliche und gleichmässige Bewegung wie der Wagen. Andererseits vollzieht sie einen vertikalen Flug nach oben und wieder nach unten.

Für einen Beobachter auf dem Wagen, bewegt sich der Boden von rechts nach links. Die Kugel schiesst senkrecht nach oben und fällt wieder senkrecht nach unten. Da ist es überhaupt nicht erstaunlich, dass die Kugel den Wagen wieder trifft. Ein Ball fällt uns auch wieder in die Hände, wenn wir ihn nach oben schiessen. Die Erde (unser “Wagen”) bewegt sich auch mit einer gewissen Geschwindigkeit. Das gilt aber für alles um uns herum, so dass wir diese Bewegung gedanklich ausklammern. Wenn wir die Bewegung des Wagens ausklammern, haben wir einfach einen vertikalen Wurf.

Scheinbar komplizierte Bewegungen können mit Hilfe der Aufteilung in zwei Bewegungen wieder vereinfacht werden.

Simulation

Stelle die Richtung des Boots so ein, dass du den Punkt am gegenüber liegenden Ufer erreichst. Du erhältst dann die gleiche Bewegung, wie der Flieger im Seitenwind.

• Simulation zusammengesetzter Bewegungen